1.SVD介绍

奇异值分解（SVD）是线性代数中一种重要的矩阵分解方法。它不光可以用于降维算法中的特征分解，还可以用于推荐系统，以及自然语言处理、图像压缩降维等领域，是很多机器学习算法的基石。

2.奇异值计算公式

3.处理图像方法

设一模板图像为A，可将图像近似表示为

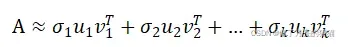
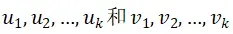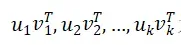图像A的大量信息体现在前k对向量中。称为图像奇异值分解的基图像。可知模板图像A是基图像的线性组合，其组合系数即为最大的k个奇异值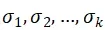。将这k个奇异值视为图像A的代数特征。

设B为任一幅图像，相对于模板图像A，将图像B表示为图像A的基图像

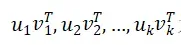的线性组合，即

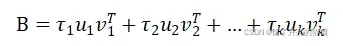
由于图像A的大量信息体现在列向量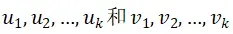中，所以组合系数

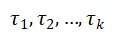描述了图像B相对于模板图像A的相似程度。于是，可以抽取组合系数

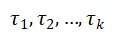作为图像的代数特征。

因为Ui，Vi分别是相互正交的列向量，上式中的组合系数由下式可得：

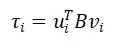
4.SVD算法

5.人脸识别实现应用

在ORL人脸库上做了实验。ORL人脸库包括40个目录，每个目录下有10张图像，每个目录表示一个不同的人，共400幅人脸图像构成。每幅图像的大小均为112*92。对每一个目录下的图像，这些图像是在不同的时间、不同的光照、不同的面部表情(睁眼/闭眼，微笑/不微笑)和面部细节(戴眼镜/不戴眼镜)环境下采集的。所有的图像是在较暗的均匀背景下拍摄的，拍摄的是正脸(有些带有略微的侧偏)。如下图展示了ORL数据库的人脸图像。

预测结果如下：

代码附录：

import cv2
import numpy as np


def imgarray():
    # 将所有图片读取为arrayList
    path = "./att_faces/s"
    ImgList = []
    for i in range(1, 41):
        for j in range(1, 10 + 1):
            imgPath = path + str(i) + "/" + str(j) + ".pgm"
            img = cv2.imread(imgPath)  # 通过opencv读取图片
            img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)  # 将图片转为灰度图
            ImgList.append(img)
    ImgList = np.array(ImgList)
    return ImgList


def decomposition(img, k):
    """
    将一张图片进行分解,将Ui*ViT存入到List中
    :param img: 传入的一张图片
    :param k: 基是U1*V1T+...+Uk*VkT
    :return:
    """
    U, E, V = np.linalg.svd(img)
    bases = []
    m, n = img.shape
    for i in range(k):
        u = np.array(U.T[i]).reshape(m, 1)
        v = np.array(V[i]).reshape(n, 1)
        bases.append((u, v))
    bases = np.array(bases, dtype=object)
    return E, bases


def getVector(img, base):
    """
    根据 τ_i=u_i^T*B*v_i 求得图像B在图像A的基下的坐标
    :param img:
    :param base:
    :return:
    """
    len = base.shape[0]
    B = img
    T = []
    for i in range(len):
        u_i, v_i = base[i]
        T.append(np.dot(np.dot(u_i.T, B), v_i))
    return np.array(T).reshape(k)


def getDistance(img, base):
    vector = getVector(img, base[1])
    baseVector = base[0][:k]
    # 计算这个人的在基下的坐标和原图的坐标之间的距离
    return np.linalg.norm(vector - baseVector)


def classify(img):
    person_number = 999
    min = 99999999
    # 计算出每个人的最小距离,如果对检测图进行检测,距离大于最小距离,则表示这张图是这个人
    for i in range(40):
        tmp_distance = getDistance(img, img_bases[i])
        if min > tmp_distance:
            person_number = i
            min = tmp_distance
    return person_number



def readImgmeans():
    for i in range(10):
        img = img_p + str(i+1) + ".pgm"
        # print(img)
        if (i==0):
            means = cv2.imread(img)
            for j in range(3):
                if (j==i+2):
                    img2 = img_p + str(j) + ".pgm"
                    means = cv2.addWeighted(means, 0.5, cv2.imread(img2), 0.5, 0)
        else:
            for j in range(11):
                if (j==i+2):
                    img2 = img_p + str(j) + ".pgm"
                    means = cv2.addWeighted(means, (j-1)/j, cv2.imread(img2), 1/j, 0)
    return np.array(means)



img_bases = []  # img_bases存放着40个人的基信息112*92,每个人的基信息中存有原有的坐标和基
k = 92  # 取前k个特征值

if __name__ == "__main__":
    img_path = "./att_faces/s"
    for m in range(1,41):
        img_p = img_path + str(m) + '/'
        abc = readImgmeans()
        baseimg = cv2.cvtColor(abc, cv2.COLOR_BGR2GRAY)  # 将图片转为灰度图
        baseimg = np.array(baseimg)
        # print(img.shape)
        E, base = decomposition(baseimg, k)
        img_bases.append((E, base))

    imgList = imgarray()
    right_num = 0  # 最终正确的数量
    test_num = len(imgList)  # 要测试的数量

    for i in range(test_num):
        classified = classify(imgList[i])
        fact = (i - i % 10) / 10
        if classified == fact:
            right_num += 1
            print(f"第{i + 1}张图像预测为第{classified + 1}类,实际为第{int(fact + 1)}类\n预测成功")
        else:
            print(f"第{i + 1}张图像预估属于第{classified + 1}类,但实际属于第{int(fact + 1)}类")
    print("准确率:%.2f%%" % (right_num / float(test_num) * 100))