作业2：BP 算法实验报告

1. 算法介绍

BP 算法全称叫做误差反向传播(Back propagation)（error Back Propagation，或者叫作误差逆传播）算法。现实任务中使用神经网络时，大多是在是使用 BP 算法进行训练。BP 算法不仅可以用户多层前馈神经网络(Multi-layer feedforward neural networks)(Feedforward Neural Networks)，还可以用于其它类型的神经网络，例如训练递归神经网络(Recursive Neural Network)。但通常说“BP 网络”时，一般是指用 BP 算法训练的多层前馈神经网络(Multi-layer feedforward neural networks)(Feedforward Neural Networks)。

BP 神经网络是这样一种神经网络模型，它是由一个输入(input)层、一个输出层(Output layer)和一个或多个隐层构成，它的激活函数(Activation Function)采用 sigmoid(Sigmoid) 函数，采用 BP 算法训练构成前馈神经网络(Feedforward Neural Networks)。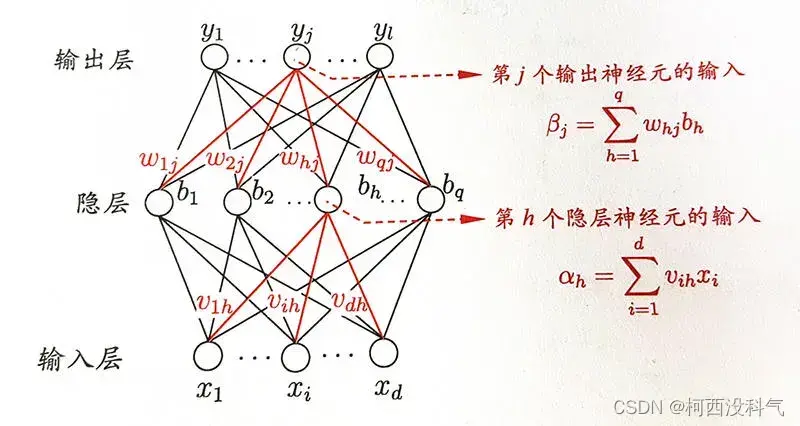

上图为一个单隐层前馈神经网络(Feedforward Neural Networks)的拓扑结构，BP神经网络算法使用梯度(gradient)下降(Gradient Descent)法（gradient descent），以单个样本的均方误差(Mean squared error)的负梯度(gradient)方向对权重进行调节。可以看出：BP算法首先将误差反向传播(Back propagation)给隐层神经元，调节隐层到输出层(Output layer)的连接权(Connection weight)重与输出层(Output layer)神经元的阈值(Threshold)；接着根据隐含层神经元的均方误差(Mean squared error)，来调节输入(input)层到隐含层的连接权(Connection weight)值与隐含层神经元的阈值(Threshold)。

2. 算法基本思想

算法的基本思想：在前馈网络(feedforward network)中，输入(input)信号通过输入(input)层输入(input)，输出层(Output layer)通过隐藏层(Hidden layer)计算输出。输出值与标记(token)值进行比较。在这个过程中，使用梯度(gradient)下降(Gradient Descent)算法来调整神经元的权重。

BP 算法包括信号的向前传播和误差的反向传播(Back propagation)两个过程。即计算误差输出时按从输入(input)到输出的方向进行，而调整权值和阈值(Threshold)则从输出到输入(input)的方向进行。

3. 算法流(stream)程

网络初始化：权重的初始值设置为一个小的随机数。
输入(input)<输入(input)向量>（前向）
首先，将<输入(input)向量>输入(input)到传输层；
被传播到输出层(Output layer)；
各神经元：求来自前层神经元的附加权值和，由传输函数决定输出值。如激活函数(Activation Function)为 Gigmoid函数 f(x) ，则输出值 = f(输入(input)和)。
将输入(input)到输出层(Output layer)，将对应的提供给输出层(Output layer)。
误差反向传播(Back propagation)的权重学习：
根据以下公式更新权重：新权重 = 旧权重 × 常数 × 𝛿 ×（前一层的神经元输出）。
当激活函数(Activation Function)为 Sigmoid 函数时，
输出层(Output layer)：𝛿=(输出)×(1−输出)×[(教师信号)−(神经元输出)]
隐层：𝛿=(输出)×(1−输出)×(来自紧接其后层的的附加权值和)
返回到 2，重复 2~4 进行权值学习。

4. 数据集(Dataset)介绍

本次实验采用经典的手写体识别数据集(Dataset)作为实验数据。MINST数据库是由Yann提供的手写数字数据库文件，其官方下载地址http://yann.lecun.com/exdb/mnist/。数据库的里的图像都是28*28大小的灰度图像，每个像素的是一个八位字节（0~255）。这个数据库主要包含了60000张的训练图像和10000张的测试图像，主要是下面的四个文件：

Training set images: train-images-idx3-ubyte.gz (9.9 MB, 解压后 47 MB, 包含 60,000 个样本)
Training set labels: train-labels-idx1-ubyte.gz (29 KB, 解压后 60 KB, 包含 60,000 个标签)
Test set images: t10k-images-idx3-ubyte.gz (1.6 MB, 解压后 7.8 MB, 包含 10,000 个样本)
Test set labels: t10k-labels-idx1-ubyte.gz (5KB, 解压后 10 KB, 包含 10,000 个标签)

部分数据集(Dataset)如下：

5. 算法实现

5.1. 算法过程

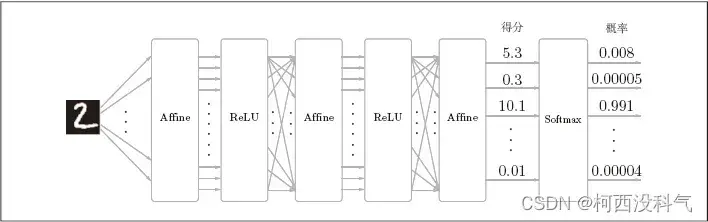
网络结构由输入(input)层、隐藏层(Hidden layer)和输出层(Output layer)组成。实际上，总共只有两个层次结构。

5.2. 数据集(Dataset)导入

定义一个读取数据集(Dataset)的方法load_mnist，方法的参数有：normalize表示将图像的像素值正规化为 0.0~1.0，one_hot_label为True的情况下，标签作为one-hot数组返回，one-hot数组是指[0,0,1,0,0,0,0,0,0,0]这样的数组；：flatten表示是否将图像展开为一维数组。最终返回(训练图像, 训练标签), (测试图像, 测试标签)。

def load_mnist(normalize=True, flatten=True, one_hot_label=False):
    if not os.path.exists(save_file):
        init_mnist()
        
    with open(save_file, 'rb') as f:
        dataset = pickle.load(f)
    
    if normalize:
        for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].astype(np.float32)
            dataset[key] /= 255.0
            
    if one_hot_label:
        dataset['train_label'] = _change_one_hot_label(dataset['train_label'])
        dataset['test_label'] = _change_one_hot_label(dataset['test_label'])
    
    if not flatten:
         for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].reshape(-1, 1, 28, 28)

    return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label'])

5.3. 层级结构设计

定义一个两层网络，输入(input)层大小为input_size，隐藏层(Hidden layer)大小为50，输出层(Output layer)大小为10。权重初始化weight_init_std默认设置为0.01。

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

隐藏层(Hidden layer)涉及权重参数和偏置项的设置。在运行算法之前，需要初始化权重参数和偏置项。权重初始化如下：

self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size) 
self.params['b2'] = np.zeros(output_size)

生成层初始化：

self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
self.layers['Relu1'] = Relu()
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])

定义损失函数(Loss function)：

def loss(self, x, t):
    y = self.predict(x)
    return self.lastLayer.forward(y, t)

定义精度：

def accuracy(self, x, t):
    y = self.predict(x)
    y = np.argmax(y, axis=1)
    if t.ndim != 1 : t = np.argmax(t, axis=1)
    
    accuracy = np.sum(y == t) / float(x.shape[0])
    return accuracy

定义预测方法：

def predict(self, x):
    for layer in self.layers.values():
        x = layer.forward(x)
    
    return x

定义梯度(gradient)下降(Gradient Descent)法gradient。 x代表输入(input)数据。 t 代表监督数据。 w1，b1，w2，b2：分别表示隐藏层(Hidden layer)的突触权重和偏差(Bias 偏置 )，以及输出层(Output layer)的突触权重和偏差(Bias 偏置 )。激活函数(Activation Function)设置为relu函数。

def gradient(self, x, t):
    self.loss(x, t)

    dout = 1
    dout = self.lastLayer.backward(dout)
    
    layers = list(self.layers.values())
    layers.reverse()
    for layer in layers:
        dout = layer.backward(dout)

    grads = {}
    grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
    grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db

    return grads

5.4. 算法迭代过程

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    grad = network.gradient(x_batch, t_batch)
    
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]
    
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)
    
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print(train_acc, test_acc)

5.5. 训练结果

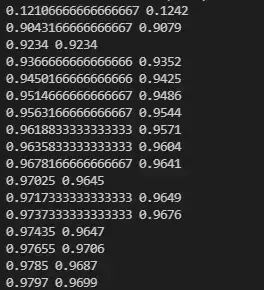
从训练结果不难看出，准确率(Precision)不断上升，最终稳定在0.9797左右。

文章出处登录后可见！

已经登录？立即刷新