高等工程数学 —— 第五章 （4）罚函数法
文章目录
外点罚函数法
做题时就是构造一个
然后计算两种情况的一阶必要条件未知量的值，若符合不等式约束就对其进行二阶必要条件验证。若成立就对
取无穷大然后得到最优解。
例：
- 这里求解
时对于
这种情况解得
,
。此时发现不满足
- 因此我们对于
这种情况求解。
- 对其进行二阶充分条件的验证
- 对
内点罚函数法
只适用于只有不等式约束的非线性最优化问题。
选取障碍函数构建罚函数，然后用一阶必要条件来求解可行点的值，再用二阶充分条件来验证。最后我们对
趋近于0来得到最后的结果。
例1：
- 此处我们可以解出
- 用二阶充分条件验证后将
例2：
例3：
广义乘子法
这个好像用的比较少一点，但是老师说不排除不考，简单应用还是要会的。
等式约束问题
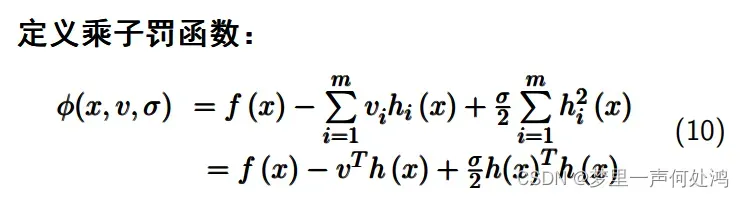
例：
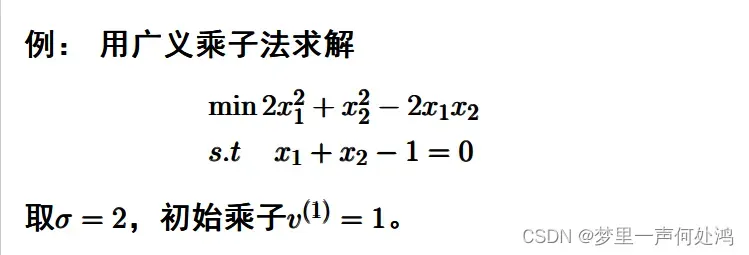
这里得到的步骤如下：
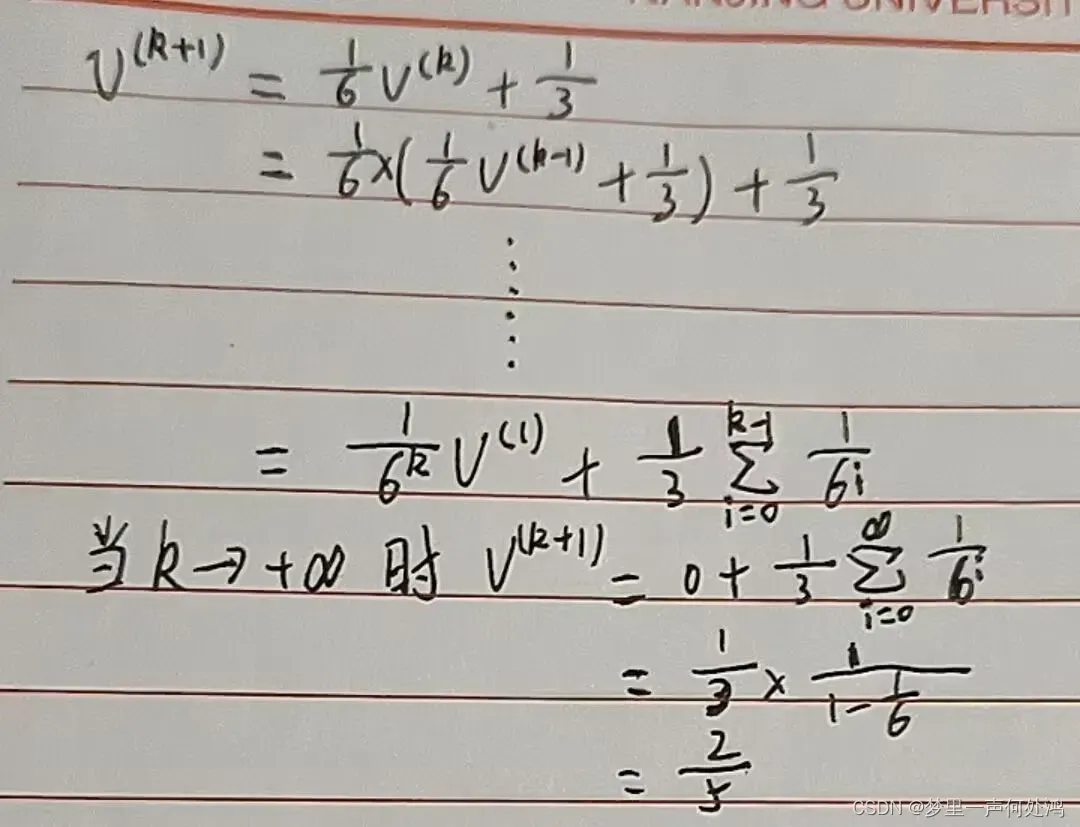
- 有一个简单的方法，我们可以令
来求解这个递增的上界。即
不等式约束问题
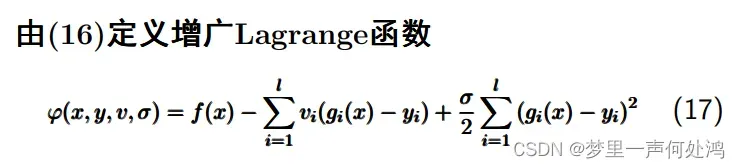
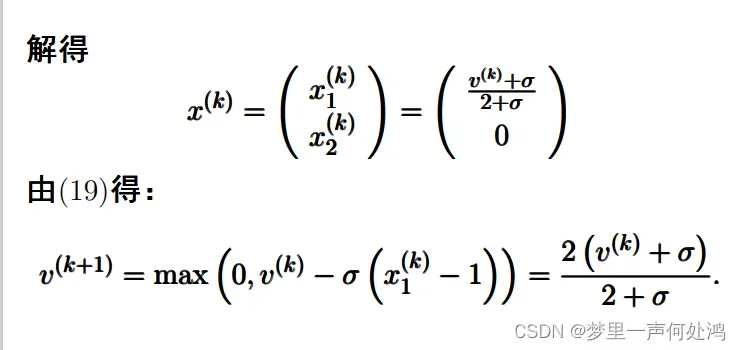
- 这里
也是令
得到的。
例：
文章出处登录后可见！
已经登录？立即刷新
