目录

1.逻辑回归

一些回归算法也可用于分类。
逻辑回归（Logistic回归，也称为Logit回归）被广泛用于估算一个实例属于某个特定类别的概率。
比如，这封电子邮件属于垃圾邮件的概率是多少？
如果预估概率超过50%，则判定该邮件属于垃圾邮件，标记为“1”，反之，标记为“0”。这样它就成了一个二元分类器。

与线性回归模型一样，逻辑回归模型也是计算输入特征的加权和（加上偏置项）
但是不同于线性回归模型直接输出结果，它输出的是结果的概率。

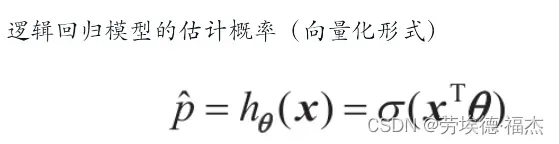
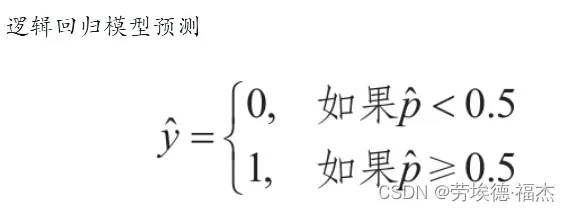
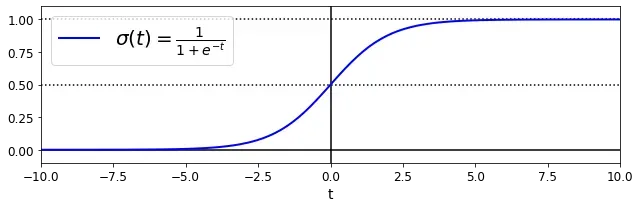
σ（·）是一个sigmoid函数，输出一个介于0和1之间的数字。 该函数图像如下。
当t＜0时，σ（t）＜0.5，模型预测结果是0
当t≥0时，σ（t）≥0.5，模型预测结果是1

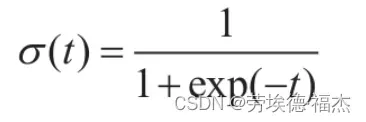
2.成本函数

当t接近于0时，-log（t）会变得非常大，所以如果模型估算一个正类实例的概率接近于0，成本将会变得很高。
同理估算出一个负类实例的概率接近1，成本也会变得非常高。
当t接近于1的时候，-log（t）接近于0，所以对一个负类实例估算出的概率接近于0。
对一个正类实例估算出的概率接近于1，而成本则都接近于0。

整个训练集的成本函数是所有训练实例的平均成本。 

这个函数没有已知的闭式方程来计算出最小化成本函数的θ值。
但是，这是个凸函数，所以通过梯度下降（或是其他任意优化算法）保证能够找出全局最小值。

成本函数关于第j个模型参数θj的偏导数方程 

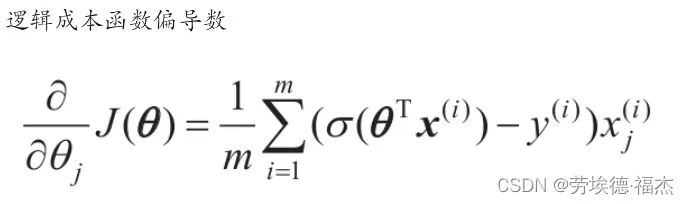
对于每个实例，它都会计算预测误差并将其乘以第j个特征值，然后计算所有训练实例的平均值。一旦你有了包含所有偏导数的梯度向量就可以使用梯度下降算法了。 

3.举例：鸢尾植物数据集

这是一个著名的数据集，共有150朵鸢尾花，分别来自三个不同品种（山鸢尾、变色鸢尾和维吉尼亚鸢尾），数据里包含花的萼片以及花瓣的长度和宽度。

我们试试仅基于花瓣宽度这一个特征，创建一个分类器来检测维吉尼亚鸢尾花。 

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.linear_model import LogisticRegression

iris = datasets.load_iris() # 加载数据
list(iris.keys()) # ['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module']

X = iris["data"][:, 3:]  # 花瓣长度
y = (iris["target"] == 2).astype(np.int32)  # 标签，是维吉尼亚鸢尾花y就是1，否则为0

log_reg = LogisticRegression(solver="lbfgs", random_state=42)
log_reg.fit(X, y) # 训练模型

看看花瓣宽度在0到3cm之间的鸢尾花，模型估算出的概率

# 绘制预测图像
X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
plt.plot(X_new, y_proba[:, 1], "g-", linewidth=2, label="Iris virginica")
plt.plot(X_new, y_proba[:, 0], "b--", linewidth=2, label="Not Iris virginica")
plt.xlabel("Petal width (cm)", fontsize=14)
plt.ylabel("Probability", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.show()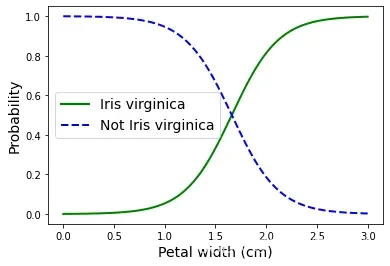

维吉尼亚鸢尾的花瓣宽度范围为1.4～2.5cm，而其他两种鸢尾花的花瓣宽度范围为0.1～1.8cm。注意，这里有一部分重叠。
在大约1.6cm处存在一个决策边界，这里“是”和“不是”的可能性都是50%，如果花瓣宽度大于1.6cm，分类器就预测它是维吉尼亚鸢尾花，否则就预测不是。

log_reg.predict([[1.7], [1.5]]) # 输出：array([1, 0], dtype=int32)

用花瓣宽度和花瓣长度这两个特征来预测新花朵是否属于维吉尼亚鸢尾

虚线表示模型估算概率为50%的点，即模型的决策边界。
每条平行线都分别代表一个模型输出的特定概率，从左下的15%到右上的90%。
根据这个模型，右上线之上的所有花朵都有超过90%的概率属于维吉尼亚鸢尾。 

from sklearn.linear_model import LogisticRegression

X = iris["data"][:, (2, 3)]  # 花瓣长度和宽度两个特征
y = (iris["target"] == 2).astype(np.int32)
log_reg = LogisticRegression(solver="lbfgs", C=10**10, random_state=42)
log_reg.fit(X, y) # 训练模型

x0, x1 = np.meshgrid(
        np.linspace(2.9, 7, 500).reshape(-1, 1),
        np.linspace(0.8, 2.7, 200).reshape(-1, 1),
    )
X_new = np.c_[x0.ravel(), x1.ravel()]
y_proba = log_reg.predict_proba(X_new)

plt.figure(figsize=(10, 4))
plt.plot(X[y==0, 0], X[y==0, 1], "bs")
plt.plot(X[y==1, 0], X[y==1, 1], "g^")

zz = y_proba[:, 1].reshape(x0.shape)
contour = plt.contour(x0, x1, zz, cmap=plt.cm.brg)
# 模型的决策边界。这是点x的集合，使得θ0+θ1x1+θ2x2=0，它定义了一条直线。
left_right = np.array([2.9, 7])
boundary = -(log_reg.coef_[0][0] * left_right + log_reg.intercept_[0]) / log_reg.coef_[0][1]

plt.clabel(contour, inline=1, fontsize=12)
plt.plot(left_right, boundary, "k--", linewidth=3)
plt.text(3.5, 1.5, "Not Iris virginica", fontsize=14, color="b", ha="center")
plt.text(6.5, 2.3, "Iris virginica", fontsize=14, color="g", ha="center")
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.axis([2.9, 7, 0.8, 2.7])
plt.show()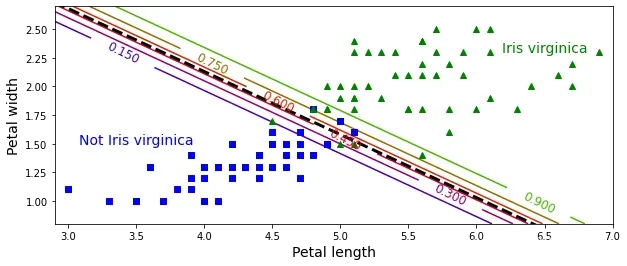

4.Softmax回归

逻辑回归模型经过推广，可以直接支持多个类别，而不需要训练并组合多个二元分类器。这就是Softmax回归，或者叫作多元逻辑回归。

原理：给定一个实例x，Softmax回归模型首先计算出每个类k的分数，然后对这些分数应用softmax函数（也叫归一化指数），估算出每个类的概率。

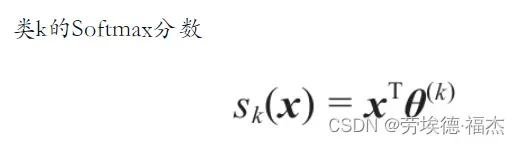
通过softmax函数来估计实例属于类k的概率 
函数x计算了实例属于k类的分数，然后计算每个分数的指数，然后对其进行归一化（除以所有指数的总和）。

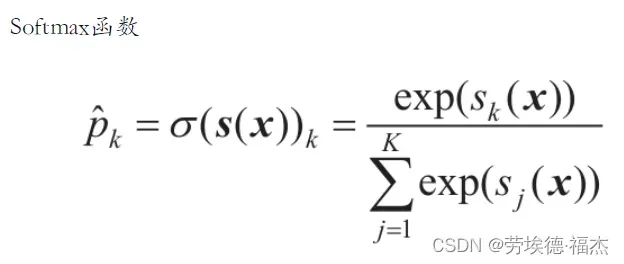
Softmax回归分类器预测具有最高估计概率的类 

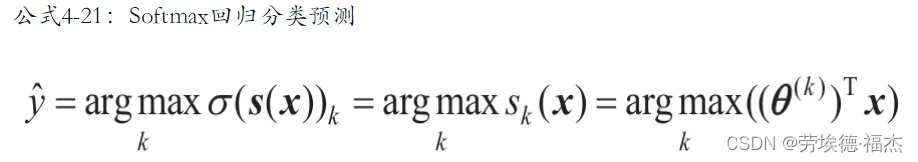
argmax运算符返回使函数最大化的变量值。
在此等式中，它返回使估计概率σ（s（x））k最大化的k值。 
Softmax回归分类器一次只能预测一个类。

成本函数（也叫作交叉熵）

交叉熵经常被用于衡量一组估算出的类概率跟目标类的匹配程度，训练目标就是最小化交叉熵

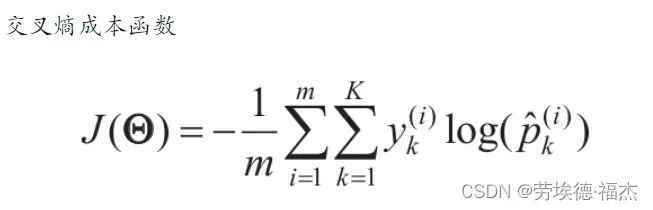
是属于类k的第i个实例的目标概率。一般而言等于1或0，具体取决于实例是否属于该类。
当只有两个类（K=2）时，此成本函数等效于逻辑回归的成本函数（公式见上）。

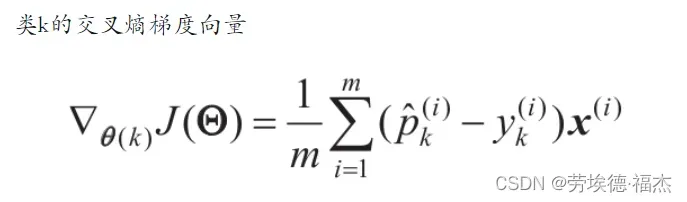
现在，你可以计算每个类的梯度向量，然后使用梯度下降（或任何其他优化算法）来找到最小化成本函数的参数矩阵Θ。

X = iris["data"][:, (2, 3)]  # 花瓣长度, 花瓣宽度
y = iris["target"]
# 设置超参数multi_class为"multinomial"，指定一个支持Softmax回归的求解器，默认使用l2正则化，可以通过超参数C进行控制
softmax_reg = LogisticRegression(multi_class="multinomial", solver="lbfgs", C=10, random_state=42)
softmax_reg.fit(X, y)

如果一朵鸢尾花，花瓣长5cm宽2cm，模型可以告诉你它的种类和是每个种类的概率。

softmax_reg.predict([[5, 2]]) # 输出：array([2])
softmax_reg.predict_proba([[5, 2]]) 
# 输出：array([[6.38014896e-07, 5.74929995e-02, 9.42506362e-01]])
# 分别对应：山鸢尾、变色鸢尾和维吉尼亚鸢尾

 绘图

x0, x1 = np.meshgrid(
        np.linspace(0, 8, 500).reshape(-1, 1),
        np.linspace(0, 3.5, 200).reshape(-1, 1),
    )
X_new = np.c_[x0.ravel(), x1.ravel()]

y_proba = softmax_reg.predict_proba(X_new)
y_predict = softmax_reg.predict(X_new)

zz1 = y_proba[:, 1].reshape(x0.shape)
zz = y_predict.reshape(x0.shape)

plt.figure(figsize=(10, 4))
plt.plot(X[y==2, 0], X[y==2, 1], "g^", label="Iris virginica")
plt.plot(X[y==1, 0], X[y==1, 1], "bs", label="Iris versicolor")
plt.plot(X[y==0, 0], X[y==0, 1], "yo", label="Iris setosa")

from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])

plt.contourf(x0, x1, zz, cmap=custom_cmap)
contour = plt.contour(x0, x1, zz1, cmap=plt.cm.brg)
plt.clabel(contour, inline=1, fontsize=12)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 7, 0, 3.5])
plt.show()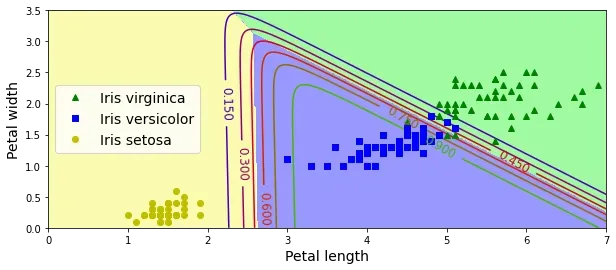

任何两个类之间的决策边界都是线性的。 
在所有决策边界相交的地方，所有类的估算概率都为33% 。