SimPy 仿真简介
第 5 部分:模拟实验的顺序采样程序

本文是与介绍使用 SimPy 框架的离散事件模拟技术的概念和方法相关的系列文章的第五篇。
在文章 4 中,我们根据指定每次运行长度的预定义事件的发生来区分终止和非终止模拟。此外,在同一篇文章中,我们开始分析模拟研究的输出数据。[0]
模拟技术习惯性地用于评估实际不存在的系统的性能,或者当希望了解存在但不需要在现实中执行它们的系统中的变化的影响时。
为此,建立和试验所研究系统的数学和/或逻辑模型,直到获得对系统行为的足够洞察以解决先前确定的业务问题。
这些实验被设计为统计实验。总结模拟实验输出数据的常用方法是使用置信区间 (CI)。在文章 4 中,我们开发了用于终止模拟的输出数据分析,使用名为固定样本大小程序的程序计算置信区间。此过程避免了输出数据的一些统计问题,但分析人员无法控制置信区间的宽度。[0][1]
另一方面,有一个名为顺序抽样的程序,它允许分析人员获得具有预定义精度水平的置信区间。
在第五篇文章中,我们将使用与文章 4 相同的示例来开发顺序程序,比较结果并说明两种程序的优缺点。
绝对与相对精度
在许多模拟研究中,常见的操作模式包括对模型进行编码和进行任意长度的单个模拟运行。从该运行中得出的性能度量被视为所研究模型的相应真实估计值。
这个过程是不正确的,因为我们使用从特定概率分布派生的随机样本(特定种子值)通过时间导航我们的模拟模型。我们获得了对我们的绩效衡量标准的估计,但它们可能有很大的差异。
因此,为了减少与单次运行相关的方差,多次运行相同的模型并对连续结果进行平均以获得点估计量 Xk。然后,根据图 1 所示的公式构建该点周围的置信区间。
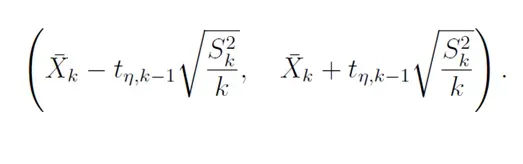
其中 k 是运行次数,tη,k−1 是自由度为 k − 1 的 t 分布的 (1 + η)/2 分位数,S²ₖ 是样本方差。
性能度量的估计精度通常是指置信区间的半宽度。它由图 2 所示的等式描述:
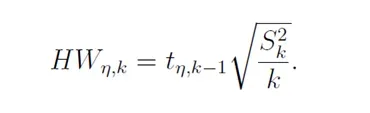
Xk 的精度可以是绝对的或相对的。
如果 X 的估计值满足│Xk — µ│= ß,则 Xk 的绝对误差为 ß(绝对精度)。
如果 X 的估计值满足 │Xk — µ│/ │µ│= γ,则 Xk 的相对误差为 γ(相对精度)。
其中 µ 是总体平均值 [1]。
在第 4 条中,我们指出固定样本程序有一个严重的缺陷,因为分析人员无法控制 IC 的宽度;所以他无法控制估计的精度。因此,如果从模拟运行生成的置信区间的半宽度必须强制满足分析人员的精度要求,我们必须使用顺序程序。[0]
Sequential Procedure
该过程假设 X1、X2、…..Xk 是来自模拟的 k 个独立同分布 (IID) 样本(性能测量)的序列。该过程的目的是获得 μ 的估计值和置信区间,置信水平为 100(1 – η),绝对精度为 ß。
绝对精度的程序如下:
1. 为置信水平选择一个值 η(通常为 90% 或 95%)。
2. 选择一个值 ß 作为该特定性能测量和该特定研究的精度要求。
3. 对模拟进行 k₀ 初始复制并设置 k = k₀。
4. 根据图 2 所示的等式计算点估计量和置信区间的半宽度。
5. 如果 HWn,k > ß,将 k 替换为 k+1,再次运行模拟,然后返回步骤 4。
6. 当 HWn,k <= ß 时,停止,以 Xk 作为点估计量,按照图 1 计算最终的置信区间。
应该注意的是,对于相对精度和 γ 的实际相对误差,我们必须在步骤 5 和 6 中计算“调整后的”相对误差 [1]:
HWn,k <= γ’, where γ’= γ/(1+ γ) [1].
Simulation with SimPy
在第 4 篇文章中,我们使用 SimPy 模拟了一个专门从事艺术品生产的工作车间。作业以每 10 小时 1 个作业的平均速度以泊松分布到达车间。该车间有两个工作站,每台机器一名操作员,所有工作都需要在两种类型的机器上进行处理。假设每个工作站的处理时间呈指数分布,平均值分别为 7 和 5。车间按照先进先出 (FIFO) 策略安排作业。[0]
在第 4 篇文章中,我们使用固定样本程序计算了某些性能指标的 CI。在本文中,我们将使用上述顺序过程计算具有绝对精度的特定性能度量。
代码如下:
首先,我们导入了以下库:Pandas、Numpy、SimPy、SciPy 和 Matplotlib。
import pandas as pd
import numpy as np
from numpy.random import RandomStateimport simpy
from scipy import stats
import matplotlib.pyplot as plt
包括一个初始化模块以指示作业到达率、表征处理时间的指数分布参数和工作站数量。数据帧 df 将用于存储中间结果。
# initialization module
# Unit of time = hoursJOBS_ARRIVAL_RATE = 1/10WORK_STATION1_MEAN = 7
WORK_STATION2_MEAN = 5NUMBER_WORK_STATION1 = 1
NUMBER_WORK_STATION2 = 1column_labels = ["Delay WK1","Delay WK2","Util. WK1",
"Util. WK2", "Avg Length WK1"]df = pd.DataFrame(columns=column_labels)
作业的到达和处理用两个生成器函数建模:1)generate_jobs; 2) 进程作业。我们在打印语句中放置了一些## 字符,因为我们仅将它们用于验证目的。[0][1]
def generate_jobs(env, arrival_stream, arrival_rate,
inital_delay = 0,
stoptime = simpy.core.Infinity,
prng = RandomState(0)): number_of_job = 0
yield env.timeout(inital_delay) #Yield the initial delay while (env.now <stoptime):
inter_arrival_time = prng.exponential(1.0 / arrival_rate)
los_station1 = prng.exponential(WORK_STATION1_MEAN)
los_station2 = prng.exponential(WORK_STATION2_MEAN) number_of_job += 1
jobpr = process_jobs(env,
'Job number: {}'.format(number_of_job), number_of_job,
los_st1 = los_station1, los_st2 = los_station2) env.process(jobpr)
yield env.timeout(inter_arrival_time)#.................................................................
def process_jobs(env, number_of_job, job_number, los_st1, los_st2): # First Workstation
##print("{} is scheduled for workstation 1
at hour {:.4f}".format(number_of_job, env.now)) workstation1_schedule_list.append(job_number)
time_workstation1_schedule_list.append(env.now) jobwk1_request = work_station1.request()
workstation1_length_list.append(len(work_station1.queue))
workstation1_timeth_list.append(env.now) yield jobwk1_request
##print("{} enters to workstation 1
at hour {:.4f}".format(job_number, env.now)) workstation1_operation_list.append(job_number)
time_workstation1_operation_list.append(env.now)
workstation1_length_list.append(len(work_station1.queue))
workstation1_timeth_list.append(env.now) ##if (env.now > jobwk1_request_time):
##print("{} has to wait {:.4f} hours".format(job_number,
env.now - jobwk1_request_time)) yield env.timeout(los_st1)
work_station1.release(jobwk1_request)
workstation1_release_list.append(job_number)
time_workstation1_release_list.append(env.now)# Second Workstation
##print("{} is scheduled for workstation 2 at hour
{:.4f}".format(job_number, env.now)) workstation2_schedule_list.append(job_number)
time_workstation2_schedule_list.append(env.now) jobwk2_request = work_station2.request()
yield jobwk2_request ##print("{} enters to workstation 2 at hour
{:.4f}".format(job_number, env.now)) workstation2_operation_list.append(job_number)
time_workstation2_operation_list.append(env.now) ##if (env.now > jobwk2_request_time):
##print("{} has to wait {:.4f} hours".format(job_number,
env.now-jobwk2_request_time)) yield env.timeout(los_st2)
work_station2.release(jobwk2_request)
workstation2_release_list.append(job_number)
time_workstation2_release_list.append(env.now)
函数 calc_measures() 允许我们计算模型的性能度量:
def calc_measures(): # Construct dataframes prior to calculations df_wk1_schdl['Job Number'] = workstation1_schedule_list
df_wk1_schdl['Job Time Sc1'] = time_workstation1_schedule_list
df_wk2_schdl['Job Number'] = workstation2_schedule_list
df_wk2_schdl['Job Time Sc2'] = time_workstation2_schedule_list df_wk1_opert['Job Number'] = workstation1_operation_list
df_wk1_opert['Job Time Op1'] = time_workstation1_operation_list
df_wk2_opert['Job Number'] = workstation2_operation_list
df_wk2_opert['Job Time Op2'] = time_workstation2_operation_list df_wk1_reles['Job Number'] = workstation1_release_list
df_wk1_reles['Job Time Rl1'] = time_workstation1_release_list
df_wk2_reles['Job Number'] = workstation2_release_list
df_wk2_reles['Job Time Rl2'] = time_workstation2_release_list df_merge = pd.merge(df_wk1_schdl, df_wk1_opert, on='Job Number', how='left')
df_merge = pd.merge(df_merge, df_wk1_reles, on='Job Number', how='left')
df_merge = pd.merge(df_merge, df_wk2_schdl, on='Job Number', how='left')
df_merge = pd.merge(df_merge, df_wk2_opert, on='Job Number', how='left')
df_merge = pd.merge(df_merge, df_wk2_reles, on='Job Number', how='left')#.......................................
# Computing measures of performance
# Average Delay in Queues df_merge['Delay Wk1'] = df_merge['Job Time Op1'] - df_merge['Job Time Sc1']
df_merge['Delay Wk2'] = df_merge['Job Time Op2'] - df_merge['Job Time Sc2']
mean_delay_wk1 = df_merge['Delay Wk1'].mean()
mean_delay_wk2 = df_merge['Delay Wk2'].mean() print(' ')
print('Measures of Performance for Run: %1d' %(run+1) )
print(' ')
print('The average delay in queue for workstation 1 is %.2f hours' % (mean_delay_wk1)) print('The average delay in queue for workstation 2 is %.2f hours' % (mean_delay_wk2))#............................................
# Utilization of the Servers
for i in range(0, len(df_merge)-1): workstation1_utilization_list.append(df_merge['Job Time Op1'][i+1] - df_merge['Job Time Rl1'][i])
workstation2_utilization_list.append(df_merge['Job Time Op2'][i+1] - df_merge['Job Time Rl2'][i]) wk2_sum_idle = np.nansum(workstation2_utilization_list)
utilization_wk1 = round((1 - wk1_sum_idle / stop_arrivals) * 100, 2)
utilization_wk2 = round((1 - wk2_sum_idle / stop_arrivals) * 100, 2) print(' ')
print('The utilization of the workstation 1 is %.2f%%' % (utilization_wk1))
print('The utilization of the workstation 2 is %.2f%%' % (utilization_wk2))
#...............................................
# Time weighted average of the queue length df_l1 = pd.DataFrame(workstation1_length_list,
columns = ['len'])
df_t1 = pd.DataFrame(workstation1_timeth_list,
columns = ['time'])
df_qlength1 = pd.concat([df_l1, df_t1], axis = 1)# use the next row to figure out how long the queue was at that length
df_qlength1['delta_time'] = df_qlength1['time'].shift(-1) - df_qlength1['time']# drop the last row because it would have an infinite time span
df_qlength1 = df_qlength1[0:-1]
len_avg_wk1 = np.average(df_qlength1['len'],
weights = df_qlength1['delta_time']) print(' ')
print('The time weighted length of the workstation 1 is %.2f' % (len_avg_wk1))
#.....................................................
# list and dataframe for final output listoflists = []
listoflists.append(round(mean_delay_wk1,2))
listoflists.append(round(mean_delay_wk2,2))
listoflists.append(utilization_wk1)
listoflists.append(utilization_wk2)
listoflists.append(round(len_avg_wk1,2)) df.loc[len(df)] = listoflists
接下来,描述用于计算置信区间的函数(calc_ICs())。当所选性能度量的置信区间的半宽度小于先前定义的绝对精度时,我们将布尔变量 (l_end) 设置为 True。
def calc_ICs(): ## confidence intervals
## define 3 global variables
global df_output, hwic, l_end mean = round(df.mean(),2)
sigma= round(df.std(ddof=1),2)
dof = len(df) -1 t_crit = np.abs(stats.t.ppf((1-confidence)/2,dof))
inf, sup = (mean-sigma*t_crit/np.sqrt(len(df)),
mean+sigma*t_crit/np.sqrt(len(df))) inf = round(inf,2)
sup = round(sup,2)
hwic= (sup-inf)/2 if hwic[0] <= abs_err_delay_wk1:
l_end = True print('')
print(round(hwic[0],2),abs_err_delay_wk1, l_end )
df_output = pd.concat([mean, sigma, inf, sup], axis=1)
print(df_output)
我们编写了函数 print_output() 来显示最近 20 次独立运行的性能度量,并打印输出数据表,指示样本均值、样本标准差以及每个性能度量的 CI 的下限和上限。
def print_output(): # Table showing measures of performance
for the last 20 independent runs df_last_20 = df.tail(20)
row_labels = ['Run' + str(i+1) for i in range(run+1-20, run+1)] fig, ax = plt.subplots(1,1)
ax.axis('tight')
ax.axis('off') runs_table = ax.table(cellText = df_last_20.values,
colLabels = df.columns, rowLabels = row_labels,
rowColours =["skyblue"]*(20),
colColours =["cyan"]*5,
cellLoc='center', loc="center") ax.set_title("Measures of Performance",
fontsize=18, y= 1.2 , pad = 4) runs_table.auto_set_font_size(False)
runs_table.set_fontsize(8)
plt.savefig(your_path +'twoWKs_perf_measures.png',
bbox_inches='tight', dpi=150)
plt.show()
#..................................................... ## Output Data Table
col_labels = ["Mean", "Std. Dev.", "Lower bound", "Upper Bound"] row_labels = ["Delay WK1 (h)","Delay WK2 (h)",
"Util. WK1 (%)","Util. WK2 (%)","Avg Length WK1"] fig, ax = plt.subplots(1,1)
ax.axis('tight')
ax.axis('off') output_table = ax.table(cellText = df_output.values,
colLabels = col_labels, rowLabels = row_labels,
rowColours =["skyblue"]*5,
colColours =["cyan"]*4,
cellLoc='center', loc="center") ax.set_title("Output data for %i independent runs" %(run+1),
fontsize=18,y= 0.8, pad = 4) output_table.auto_set_font_size(False)
output_table.set_fontsize(8)
plt.savefig(your_path +'twoWKs_output_perf_measures.png',
bbox_inches='tight', dpi=150)
plt.show()
对于 90% 的置信度、1.0 的绝对精度和 k₀ = 10(如果运行 >= 10:),模拟算法的核心是:
confidence = 0.90
abs_err_delay_wk1 = 1.00
l_end = Falseinit_numb_of_runs = 500
numb_of_runs = init_numb_of_runsseed_value = 2345
prbnumgen = RandomState(seed_value)
hours_run_sim = 30 * 24
stop_arrivals = 720 ## for the verification stepfor run in range(numb_of_runs): workstation1_schedule_list, workstation2_schedule_list = [],[]
workstation1_operation_list,workstation2_operation_list= [],[]
workstation1_release_list, workstation2_release_list = [],[] time_workstation1_schedule_list, time_workstation2_schedule_list = [],[]
time_workstation1_operation_list,time_workstation2_operation_list = [],[]
time_workstation1_release_list, time_workstation2_release_list = [],[] workstation1_length_list, workstation1_utilization_list = [],[]
workstation1_timeth_list, workstation2_utilization_list = [],[] mean_delay_wk1, mean_delay_wk2 = [],[]
utilization_wk1, utilization_wk2 = [],[]
len_avg_wk1, len_avg_wk2 = [],[]
listoflists = [] df_wk1_schdl = pd.DataFrame(columns = ['Job Number', 'Job Time Sc1'])
df_wk2_schdl = pd.DataFrame(columns = ['Job Number', 'Job Time Sc2'])
df_wk1_opert = pd.DataFrame(columns = ['Job Number', 'Job Time Op1'])
df_wk2_opert = pd.DataFrame(columns = ['Job Number', 'Job Time Op2'])
df_wk1_reles = pd.DataFrame(columns = ['Job Number', 'Job Time Rl1'])
df_wk2_reles = pd.DataFrame(columns = ['Job Number', 'Job Time Rl2']) # Set up the simulation environment
env = simpy.Environment() work_station1 = simpy.Resource(env, NUMBER_WORK_STATION1)
work_station2 = simpy.Resource(env, NUMBER_WORK_STATION2) env.process(generate_jobs(env, "Type1", JOBS_ARRIVAL_RATE, 0,
stop_arrivals, prbnumgen)) env.run(until = hours_run_sim)
calc_measures() if run >= 10:
calc_ICs() if l_end == True:
print_output()
break
Analysis
在第 4 篇文章中,我们使用固定样本量程序计算了一些性能指标的置信区间。我们在每次运行中使用不同的随机数流进行了 10 次独立复制。表 1 显示了工作站 1 的延迟、工作站 2 的延迟、工作站 1 和 2 忙碌的时间百分比以及时间-队列的加权平均长度 1. 分析师认为某些置信区间太大而对业务目的没有意义。[0]
由于分析师无法控制 CI 的精度,他决定使用前面代码中指示的顺序过程。他为工作站 1 的延迟设置了 90% 的置信水平和 1.0 的绝对精度。他选择 30*24 = 720 小时的模拟时间作为终止模拟的终止事件,并且两个工作站都空闲作为初始条件. for 循环外的种子值 2345 (for run in range(numb_of_runs):) 用于实现跨运行的统计独立性。
表 2 显示了研究中最后 20 次独立运行的性能测量值。我们需要 208 次运行才能获得所需的绝对精度。表 2 中显示的估计值的巨大差异清楚地表明了模拟输出数据的随机性以及计算每个性能度量的 CI 的需要。
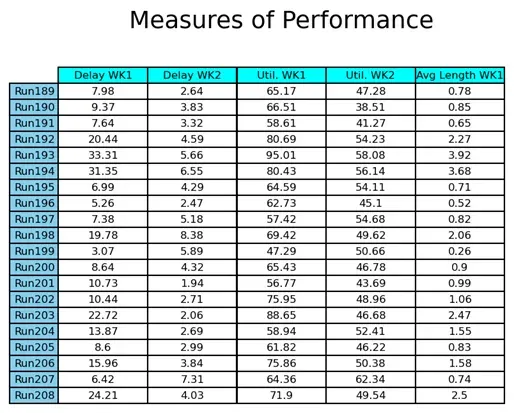
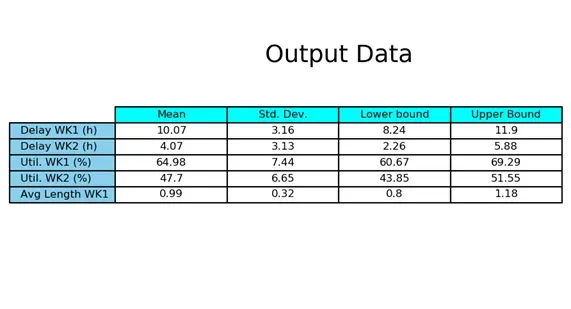
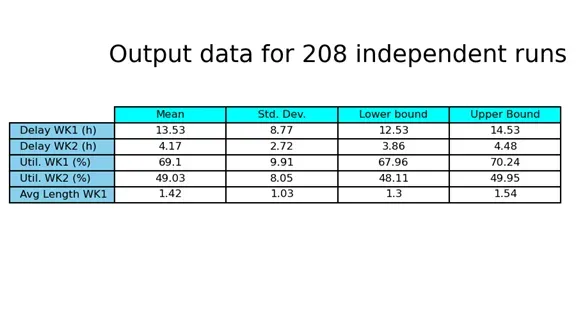
表 3 总结了模拟研究的输出数据。它显示了 208 次独立运行后我们衡量性能的置信区间的平均值、标准差和上下限。我们以大约 90% 的置信度声称工作站 1 的延迟包含在区间 [12.53, 14.53] 小时内。工位 1 的延迟置信区间宽度等于 2,因此 IC 的半宽度满足分析人员的精度要求。从固定样本程序获得的值可以观察到一个非常重要的差异,用于该性能度量。
置信区间定义为包含具有指定概率的真值的区域。我们必须为要构建的每个 CI 定义置信度。还有一个与 CI 相关的重要量:覆盖概率。置信水平是过程的标称覆盖概率。覆盖概率是区间包含真实均值的实际概率。如果满足用于推导置信区间的所有假设,则名义覆盖概率将等于覆盖概率。但是,如果不满足某些假设,则实际覆盖概率可能小于或大于名义覆盖概率 [2]。
顺序过程虽然显着减小了 IC 的半宽,但在覆盖范围方面并不总是表现良好。覆盖范围可能不同,因为在模拟实验期间未满足 CI 的假设,或者输出数据的分布与程序假设的分布不同。此外,覆盖率对 ß 的选择非常敏感。在任何情况下,我们都必须意识到使用顺序程序可能导致严重损失。
在接下来的文章中,我们将继续分析模拟研究中存在的这些和其他重要的统计问题。
[1]:法律,上午& Kelton, W.D. (2000) 仿真建模和分析。麦格劳希尔,波士顿。
[2]:https://en.wikipedia.org/wiki/Coverage_probability[0]
文章出处登录后可见!
