机器学习:基于支持向量机(SVM)进行人脸识别预测
作者:AOAIYI
作者简介:Python领域新星作者、多项比赛获奖者:AOAIYI首页
😊😊😊如果觉得文章不错或能帮助到你学习,可以点赞👍收藏📁评论📒+关注哦!👍👍👍
📜📜📜如果有小伙伴需要数据集和学习交流,文章下方有交流学习区!一起学习进步!💪
| 专栏案例:机器学习 |
|---|
| 机器学习:基于逻辑回归对某银行客户违约预测分析 |
| 机器学习:学习k-近邻(KNN)模型建立、使用和评价 |
| 机器学习:基于主成分分析(PCA)对数据降维 |
| 决策树算法分析天气、周末和促销活动对销量的影响 |
| 机器学习:线性回归分析女性身高与体重之间的关系 |
文章目录
一、实验目的
1.理解SVM原理
2.掌握scikit-learn操作SVM的方法
二、实验原理
SVM(Support Vector Machine)指的是支持向量机,是常见的一种判别方法。在机器学习领域,是一个有监督的学习模型,通常用来进行模式识别、分类以及回归分析。通过寻求结构化风险最小来提高学习机泛化能力,实现经验风险和置信范围的最小化,从而达到在统计样本量较少的情况下,亦能获得良好统计规律的目的。通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,即支持向量机的学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。
具体原理:
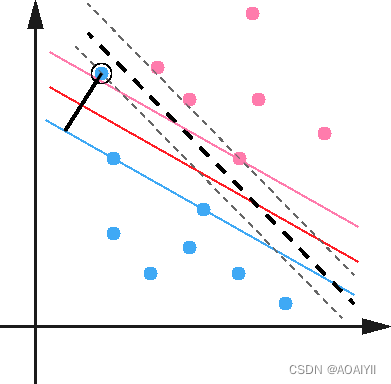
1.在n维空间中找到一个分类超平面,将空间上的点分类。如下图是线性分类的例子。
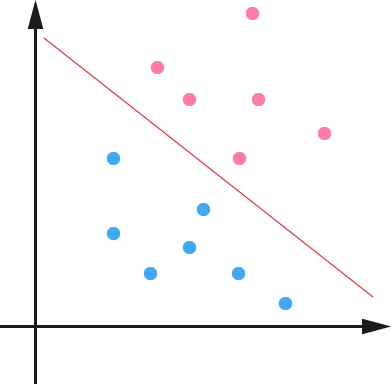
2.一般而言,一个点距离超平面的远近可以表示为分类预测的确信或准确程度。SVM就是要最大化这个间隔值。而在虚线上的点便叫做支持向量Supprot Verctor。
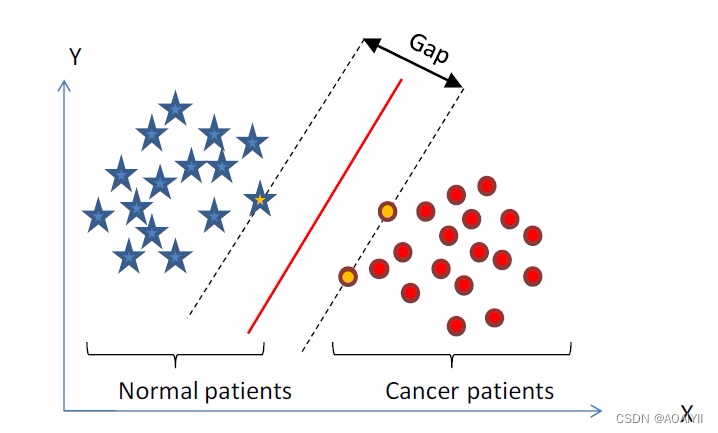
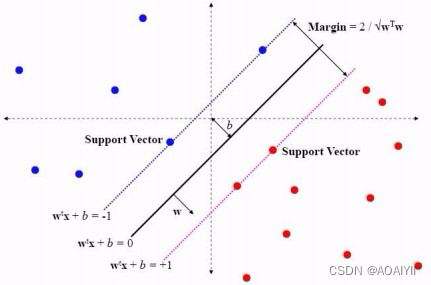
3.实际上,我们会经常遇到线性不可分的样例,此时,我们的常用做法是把样例特征映射到高维空间中去(如下图);
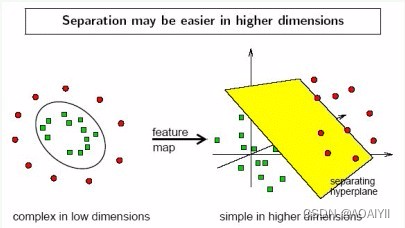
4.线性不可分映射到高维空间,可能会导致维度大小高到可怕(19维乃至无穷维的例子),导致计算复杂。核函数的价值在于它虽然也是讲特征进行从低维到高维的转换,但核函数绝就绝在它事先在低维上进行计算,而将实质上的分类效果表现在了高维上,也就如上文所说的避免了直接在高维空间中的复杂计算。
5.使用松弛变量处理数据噪音
sklearn中SVM的结构,及各个参数说明如下
sklearn.svm.SVC :
C:C-SVC的惩罚参数C?默认值是1.0
C越大,相当于惩罚松弛变量,希望松弛变量接近0,即对误分类的惩罚增大,趋向于对训练集全分对的情况,这样对训练集测试时准确率很高,但泛化能力弱。C值小,对误分类的惩罚减小,允许容错,将他们当成噪声点,泛化能力较强。
kernel :核函数,默认是rbf,可以是‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’
0 – 线性:u’v
1 – 多项式:(gamma*u’v + coef0)^degree
2 – RBF函数:exp(-gamma|u-v|^2)
3 –sigmoid:tanh(gammau’v + coef0)
degree :多项式poly函数的维度,默认是3,选择其他核函数时会被忽略。
gamma : ‘rbf’,‘poly’ 和‘sigmoid’的核函数参数。默认是’auto’,则会选择1/n_features
coef0 :核函数的常数项。对于‘poly’和 ‘sigmoid’有用。
probability :是否采用概率估计?.默认为False
shrinking :是否采用shrinking heuristic方法,默认为true
tol :停止训练的误差值大小,默认为1e-3
cache_size :核函数cache缓存大小,默认为200
class_weight :类别的权重,字典形式传递。设置第几类的参数C为weightC(C-SVC中的C)
verbose :允许冗余输出?
max_iter :最大迭代次数。-1为无限制。
decision_function_shape :‘ovo’, ‘ovr’ or None, default=None3
random_state :数据洗牌时的种子值,int值
主要调节的参数有:C、kernel、degree、gamma、coef0。
三、实验环境
Python 3.9
Jupyter
四、实验内容
利用sklearn中的svm支持向量机对fetch_lfw_people数据进行人脸识别,并将预测结果可视化。
五、实验步骤
1.准备数据
1.首先需要的数据有:joblib、lfw_funneled、pairs.txt、pairsDevTest.txt、pairsDevTrain.txt
注意:也可以直接使用fetch_lfw_people这个函数是用来加载lfw人脸识别数据集的函数。
2.其次在其路径中创建一个文件
3.最后在文件里创建一个ipynb文件
SVM(Support Vector Machine)指的是支持向量机,是常见的一种判别方法。在机器学习领域,是一个有监督的学习模型,通常用来进行模式识别、分类以及回归分析。
2.业务理解
利用sklearn中的svm支持向量机做人脸识别
该数据集是在互联网上收集的著名人物的JPEG图片的集合,所有详细信息可在官方网站上获得:
http://scikit-learn.org/stable/datasets/labeled_faces.html
http://vis-www.cs.umass.edu/lfw/
每张照片都以一张脸为中心。每个通道的每个像素(RGB中的颜色)由范围为0.0-1.0的浮点编码。
该任务称为面部识别(或识别):给定面部图片,找到给定训练集(图库)的人的姓名。
3.数据理解
1.在刚才新建的ipynb文件中,编写代码,导入数据
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns;sns.set()
from matplotlib.font_manager import FontProperties
#导入fetch_lfw_people
from sklearn.datasets import fetch_lfw_people
#fetch_lfw_people函数加载人脸识别数据集
faces = fetch_lfw_people(min_faces_per_person=60)
#输出人名
print(faces.target_names)
#输出人脸数据结构
print(faces.images.shape)

说明:
fetch_lfw_people这个函数是用来加载lfw人脸识别数据集的函数,返回data,images,target,target_names.分别是向量化的人脸数据,人脸,人脸对应的人名编号,人名
关于此函数参数的描述:min_faces_per_person:提取的数据集将只保留至少具有min_faces_per_person个不同人的图片
具体数据可参考官方文档:http://scikit-learn.org/stable/modules/generated/sklearn.datasets.fetch_lfw_people.html
2.绘制图形
#使用subplots 画图
fig,ax = plt.subplots(3,5)
#在每一行上绘制子图
for i,axi in enumerate(ax.flat):
axi.imshow(faces.images[i],cmap="bone")
axi.set(xticks=[],yticks=[],xlabel=faces.target_names[faces.target[i]])
plt.show()
注释: 使用subplots会返回两个东西,一个是matplotlib.figure.Figure,也就是fig,另一个是Axes object or array of Axes objects,也就是代码中的ax;把f理解为你的大图,把ax理解为包含很多小图对象的array;所以下面的代码就使用ax[0][0]这种从ax中取出实际要画图的小图对象;画出的图如下所示;
4.数据划分为测试集和训练集
1.划分训练集和测试集
from sklearn.model_selection import train_test_split
Xtrain,Xtest,ytrain,ytest=train_test_split(faces.data,faces.target,random_state=42)
Xtrain

5.模型构建
1.建立模型,计算人脸数据集上的PCA(特征脸)(处理为标记的)
from sklearn.svm import SVC
from sklearn.decomposition import PCA
from sklearn.pipeline import make_pipeline
pca = PCA(n_components=150,whiten=True,random_state=42,svd_solver='randomized')
svc = SVC(kernel='rbf',class_weight='balanced')
model = make_pipeline(pca,svc)
说明:PCA主要是通过奇异值分解将数据映射到低纬度的空间(正交去相关)。PCA在数据降维,数据压缩,特征提取有很大贡献。在此,我们利用PCA提取150个主要特征,并将人脸数据全部映射到150维度,通过这150维人脸特征作为训练数据训练基于rbf kernel的SVM,模型差不多有0.85的准确率
6.参数调整
1.param_grid把参数设置成了不同的值,C:权重;gamma:多少的特征点将被使用,因为我们不知道多少特征点最好,选择了不同的组合
#参数调整
from sklearn.model_selection import GridSearchCV
param_grid = {"svc__C":[1,5,10,50],"svc__gamma":[0.0001,0.0005,0.001,0.005]}
#把所有我们所列参数的组合都放在SVC里面进行计算,最后看出哪一组函数的表现度最好
grid = GridSearchCV(model,param_grid)
%time grid.fit(Xtrain,ytrain)
print(grid.best_params_)
说明:svc__C为10svc__gamma为0.001表现度最好
7.预测测试集的人名编号
model = grid.best_estimator_
model

预测测试集:
yfit = model.predict(Xtest)
yfit

说明:结果为预测的人名编号
8.显示预测结果
1.数据可视化,把需要打印的图打印出来,预测的结果和实际结果一致,人名字体颜色为黑色,否则为红色
#显示预测结果
fig,ax = plt.subplots(4,6)
for i,axi in enumerate(ax.flat):
axi.imshow(Xtest[i].reshape(62,47),cmap="bone")
axi.set(xticks=[],yticks=[])
#设置y轴上的标签
axi.set_ylabel(faces.target_names[yfit[i]].split()[-1],color="black" if yfit[i]==ytest[i] else "red")
fig.suptitle("Incorrect Labels in Red",size=14)
plt.show()
9.分析预测结果的准确性
使用seaborn.heatmap绘制颜色编码矩阵
解释:seaborn.heatmap()将矩形数据绘制为颜色编码矩阵。
seaborn.heatmap(data,vmin = None,vmax = None,cmap = None,center = None,robust = False,annot = None,fmt =‘。2g’,annot_kws = None,linewidths = 0,linecolor =‘white’,cbar =是的,cbar_kws =无,cbar_ax =无,square = False,xticklabels =‘auto’,yticklabels =‘auto’,mask = None,ax = None,** kwargs )
重要参数说明:
-
data:矩形数据集
-
square:布尔值,可选,如果为True,则将Axes方面设置为“相等”,以使每个单元格为方形
-
annot:bool或矩形数据集,可选,如果为True,则在每个单元格中写入数据值。如果数组具有相同的形状data,则使用此选项来注释热图而不是原始数据。
-
fmt:string,可选,添加注释时要使用的字符串格式代码。
-
cbar:布尔值,可选,是否绘制颜色条
-
xticklabels,yticklabels:“auto”,bool,list-like或int,optional。如果为True,则绘制数据框的列名称。如果为False,则不绘制列名称。如果是列表,则将这些替代标签绘制为xticklabels。如果是整数,则使用列名称,但仅绘制每个n标签。如果是“自动”,请尝试密集绘制不重叠的标签
#分析预测结果的准确性
from sklearn.metrics import confusion_matrix
#混淆矩阵
mat = confusion_matrix(ytest,yfit)
#绘制热图
sns.heatmap(mat.T,square=True,annot=True,fmt="d",cbar=False,xticklabels=faces.target_names,yticklabels=faces.target_names)
plt.rcParams["font.family"]="SimHei"
plt.xlabel("真实值")
plt.ylabel("预测值")
plt.show()
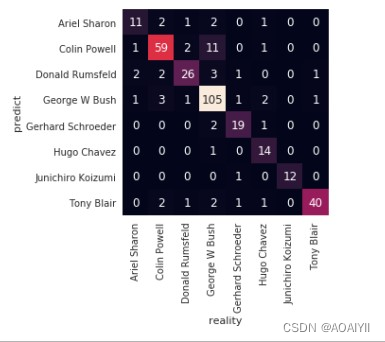
10.完整代码
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns;sns.set()
from matplotlib.font_manager import FontProperties
#导入fetch_lfw_people
from sklearn.datasets import fetch_lfw_people
#fetch_lfw_people函数加载人脸识别数据集
faces = fetch_lfw_people(min_faces_per_person=60)
#输出人名
print(faces.target_names)
#输出人脸数据结构
print(faces.images.shape)
#使用subplots 画图
fig,ax = plt.subplots(3,5)
#在每一行上绘制子图
for i,axi in enumerate(ax.flat):
axi.imshow(faces.images[i],cmap="bone")
axi.set(xticks=[],yticks=[],xlabel=faces.target_names[faces.target[i]])
plt.show()
#划分训练集和测试集
from sklearn.model_selection import train_test_split
Xtrain,Xtest,ytrain,ytest=train_test_split(faces.data,faces.target,random_state=42)
Xtrain
#建模
from sklearn.svm import SVC
from sklearn.decomposition import PCA
from sklearn.pipeline import make_pipeline
#计算人脸数据集上的PCA(特征脸)(处理为未标记的)
pca = PCA(n_components=150,whiten=True,random_state=42,svd_solver='randomized')
svc = SVC(kernel='rbf',class_weight='balanced')
model = make_pipeline(pca,svc)
#参数调整
from sklearn.model_selection import GridSearchCV
param_grid = {"svc__C":[1,5,10,50],"svc__gamma":[0.0001,0.0005,0.001,0.005]}
#把所有我们所列参数的组合都放在SVC里面进行计算,最后看出哪一组函数的表现度最好
grid = GridSearchCV(model,param_grid)
%time grid.fit(Xtrain,ytrain)
print(grid.best_params_)
model = grid.best_estimator_
model
yfit = model.predict(Xtest)
yfit
#显示预测结果
fig,ax = plt.subplots(4,6)
for i,axi in enumerate(ax.flat):
axi.imshow(Xtest[i].reshape(62,47),cmap="bone")
axi.set(xticks=[],yticks=[])
#设置y轴上的标签
axi.set_ylabel(faces.target_names[yfit[i]].split()[-1],color="black" if yfit[i]==ytest[i] else "red")
fig.suptitle("Incorrect Labels in Red",size=14)
plt.show()
#分析预测结果的准确性
from sklearn.metrics import confusion_matrix
#混淆矩阵
mat = confusion_matrix(ytest,yfit)
#绘制热图
sns.heatmap(mat.T,square=True,annot=True,fmt="d",cbar=False,xticklabels=faces.target_names,yticklabels=faces.target_names)
plt.rcParams["font.family"]="SimHei"
plt.xlabel("真实值")
plt.ylabel("预测值")
plt.show()
总结
逻辑回归可以分为线性与非线性,也可以根据类的个数分为二分类与多分类问题,使用时需要灵活应用,能够构造损失函数并求梯度,同时能够用算法实现并进行训练预测。
事实上,细心的同学会发现,在逻辑回归中,我们发现是多个输入(即p个指标),最终输出一个结果(0或1),处理过程是输入乘上权重w加偏置b,再对结果用sigmoid 函数处理,这个过程其实很接近于神经网络了,而逻辑回归的模型更接近于感知机。对于神经网络,它不只有输入和输出两层,而且增加了更多的隐藏层,每一层的处理结果都作为下一层的输入,那么它的损失函数与梯度的求解也将更加复杂,模型也复杂许多。
文章出处登录后可见!
