SGM半全局匹配(Semi-Global Matching)
参考论文:H Hirschmüller. Stereo Processing by Semiglobal Matching and Mutual Information[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 30.
参考博文:立体视觉入门指南(7):立体匹配_闲情逸致~-CSDN博客
内容
SGM半全局匹配(Semi-Global Matching)
算法的前提
成本空间
census变换
成本聚合
视差计算
左右一致性(L-R Check)
二次曲线拟合像素视差
SIMD256优化
多线程优化
同时计算8或者16个最小代价路径计算
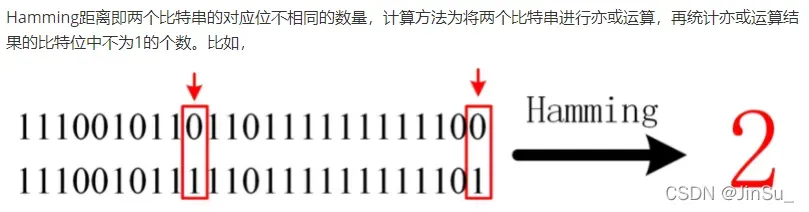
计算代价(基于Hamming距离)
算法的前提
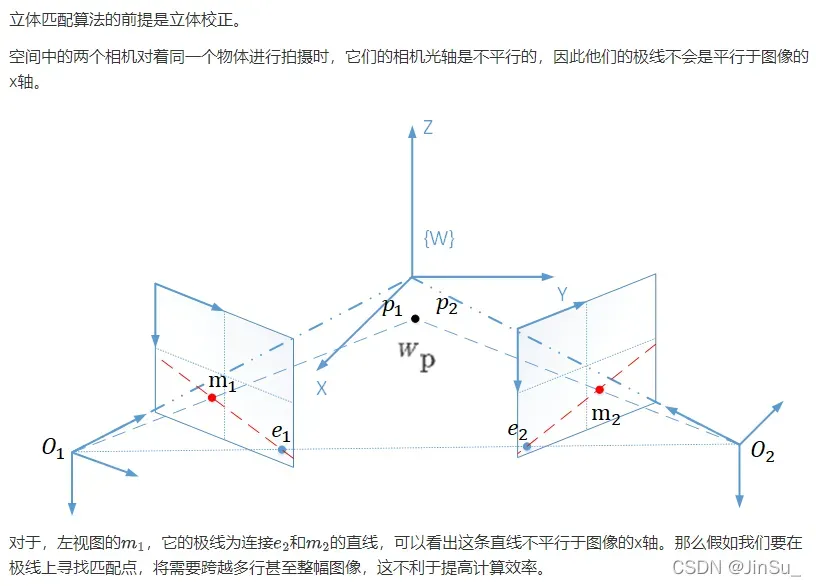
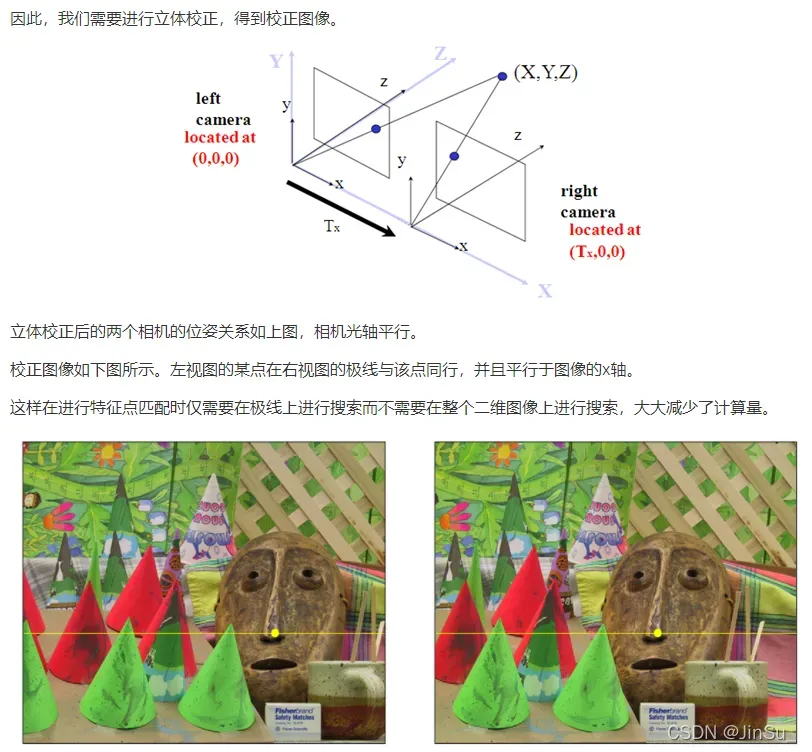
立体校正博文:
opencv双目标定+立体校正+立体匹配(源码&讲解)_三维视觉工作室的博客-CSDN博客_opencv 双目标定
双目视觉之立体校正_XiaoJie的博客-CSDN博客
【立体视觉】双目立体标定与立体校正_把岁月化成歌 留在博客-CSDN博客_立体校正

成本空间

互信息的代价计算,参考:【理论恒叨】【立体匹配系列】经典SGM:(1)匹配代价计算之互信息(MI)_闲情逸致~-CSDN博客_理论恒叨
census变换
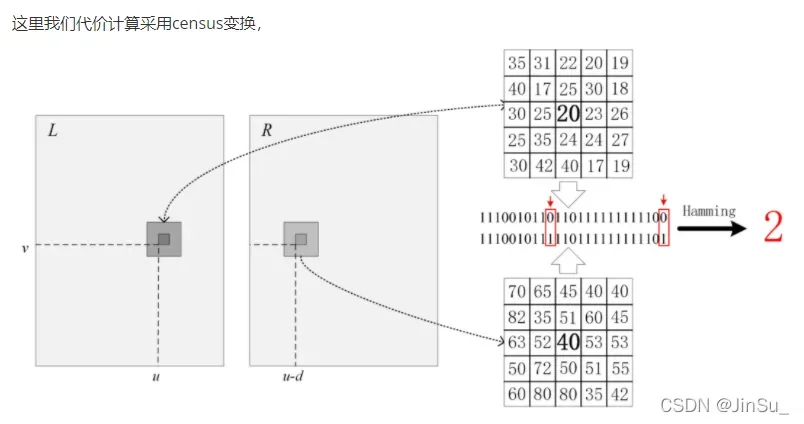
特征提取:

距离度量:
成本聚合


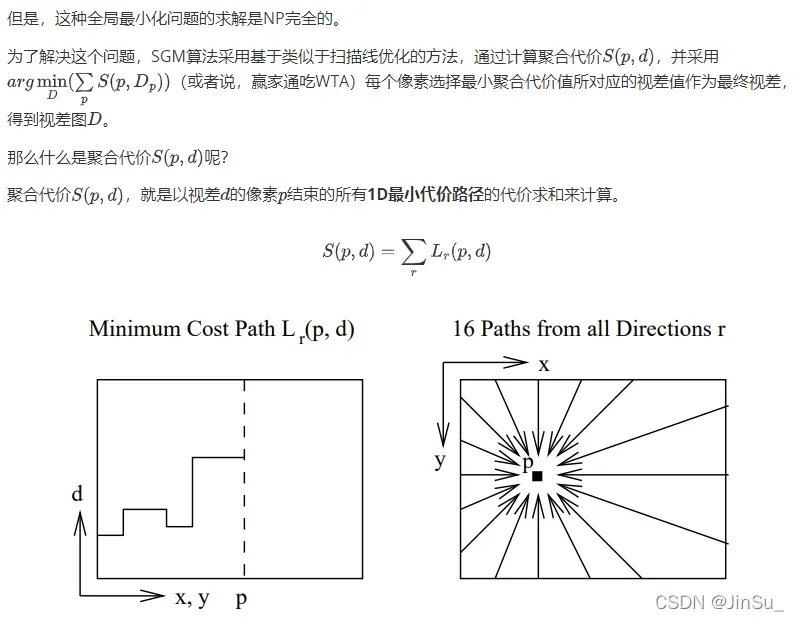

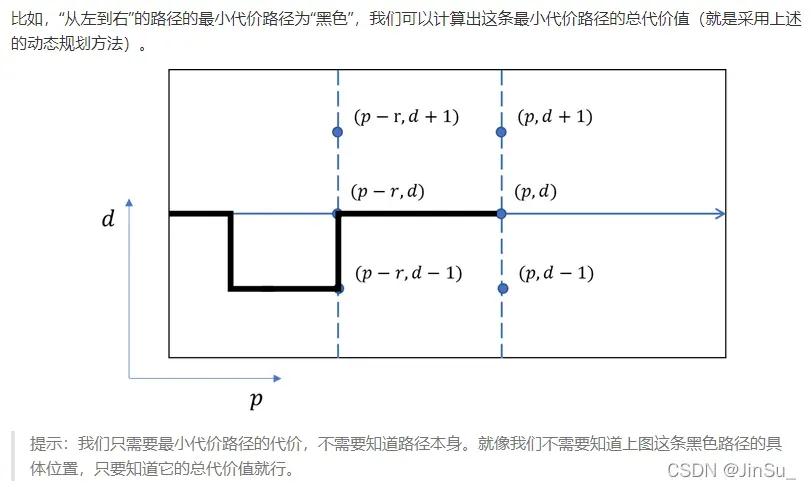

视差计算
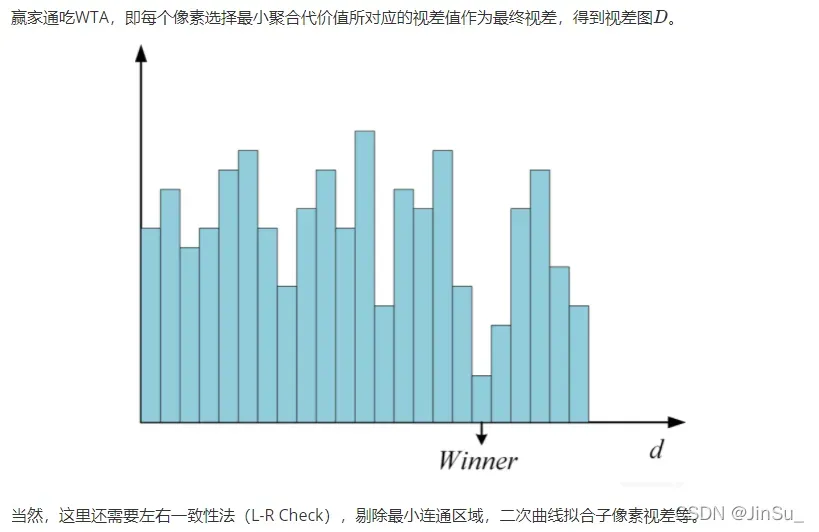
左右一致性(L-R Check)

二次曲线拟合像素视差
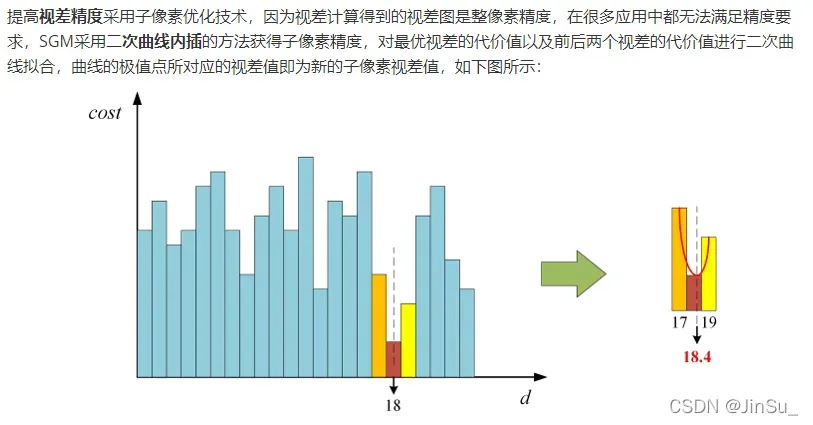
我参考了李迎松博士的关于SGM的代码实现,并且根据算法的规则结构设计simd256优化和多线程优化:
参考代码:https://github.com/ethan-li-coding/SemiGlobalMatching
SIMD256优化
SIMD256入门博文参见:【学习体会】SIMD256技术 & AVX2指令集 & 使用immintrin的api和数据结构编写测试实例 & immintrin的api解析_LeonJin的博客-CSDN博客

typedef uint16_t pixeltype; // 无符号16位整数
typedef __m256i simd256type;
#define simd256_set1(_value) (_mm256_set1_epi16(_value))
#define simd256_store(_index,_value) (_mm256_storeu_si256(_index,_value))
#define simd256_load(_index) (_mm256_loadu_si256(_index))
#define simd256_min(_value1,_value2) (_mm256_min_epu16(_value1,_value2))
#define simd256_add(_value1,_value2) (_mm256_add_epi16(_value1,_value2))
#define simd256_sub(_value1,_value2) (_mm256_sub_epi16(_value1,_value2))
#define MAX_VALUE UINT16_MAX例如: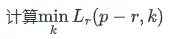
uint8 mincost_last_path = UINT8_MAX;
mincost_last = simd256_set1(mincost_last_path);
for (int i = 1; i < disp_range + 1; i += step) {
for (size_t k = 0; k < step; k++) {
cost_list[k] = cost_last_path[i + k];
}
cost = simd256_load((simd256type*)cost_list);
mincost_last = simd256_min(mincost_last, cost);
}
simd256_store((simd256type*)tmp, mincost_last);
for (size_t k = 0; k < step; k++) {
mincost_last_path = std::min(mincost_last_path, tmp[k]);
}优化”从左到右”的最小代价路径计算sgm_util::CostAggregateLeftRight
void sgm_util::CostAggregateLeftRight(const uint8* img_data, const sint32& width, const sint32& height, const sint32& min_disparity, const sint32& max_disparity,
const sint32& p1, const sint32& p2_init, const uint8* cost_init, uint8* cost_aggr, bool is_forward)
{
auto start = std::chrono::steady_clock::now();
assert(width > 0 && height > 0 && max_disparity > min_disparity);
// 视差范围
const sint32 disp_range = max_disparity - min_disparity;
// P1,P2
const auto& P1 = p1;
const auto& P2_Init = p2_init;
// 正向(左->右) :is_forward = true ; direction = 1
// 反向(右->左) :is_forward = false; direction = -1;
const sint32 direction = is_forward ? 1 : -1;
size_t step = 256 / (sizeof(pixeltype) * 8);
pixeltype* cost_list = (pixeltype*)sgm_util::aligned_malloc(sizeof(pixeltype)*step,32);
pixeltype* l1_list = (pixeltype*)sgm_util::aligned_malloc(sizeof(pixeltype)*step,32);
pixeltype* l2_list = (pixeltype*)sgm_util::aligned_malloc(sizeof(pixeltype)*step,32);
pixeltype* l3_list = (pixeltype*)sgm_util::aligned_malloc(sizeof(pixeltype)*step,32);
pixeltype* l4_list = (pixeltype*)sgm_util::aligned_malloc(sizeof(pixeltype)*step,32);
pixeltype* cost_s_list = (pixeltype*)sgm_util::aligned_malloc(sizeof(pixeltype)*step,32);
pixeltype* tmp = (pixeltype*)sgm_util::aligned_malloc(sizeof(pixeltype)*step,32);
simd256type cost, l1, l2, l3, l4, cost_s, mincost_last;
uint8* index;
// 聚合
for (sint32 i = 0u; i < height; i++) {
// 路径头为每一行的首(尾,dir=-1)列像素
auto cost_init_row = (is_forward) ? (cost_init + i * width * disp_range) : (cost_init + i * width * disp_range + (width - 1) * disp_range);
auto cost_aggr_row = (is_forward) ? (cost_aggr + i * width * disp_range) : (cost_aggr + i * width * disp_range + (width - 1) * disp_range);
auto img_row = (is_forward) ? (img_data + i * width) : (img_data + i * width + width - 1);
// 路径上当前灰度值和上一个灰度值
uint8 gray = *img_row;
uint8 gray_last = *img_row;
// 路径上上个像素的代价数组,多两个元素是为了避免边界溢出(首尾各多一个)
std::vector<uint8> cost_last_path(disp_range + 2, UINT8_MAX);
// 初始化:第一个像素的聚合代价值等于初始代价值
memcpy(cost_aggr_row, cost_init_row, disp_range * sizeof(uint8));
memcpy(&cost_last_path[1], cost_aggr_row, disp_range * sizeof(uint8));
cost_init_row += direction * disp_range;
cost_aggr_row += direction * disp_range;
img_row += direction;
// 路径上,"上个像素"的最小代价值
uint8 mincost_last_path = UINT8_MAX;
mincost_last = simd256_set1(mincost_last_path);
for (int i = 1; i < disp_range + 1; i += step) {
for (size_t k = 0; k < step; k++) {
cost_list[k] = cost_last_path[i + k];
}
cost = simd256_load((simd256type*)cost_list);
mincost_last = simd256_min(mincost_last, cost);
}
simd256_store((simd256type*)tmp, mincost_last);
for (size_t k = 0; k < step; k++) {
mincost_last_path = std::min(mincost_last_path, tmp[k]);
}
// 自方向上第2个像素开始按顺序聚合
for (sint32 j = 0; j < width - 1; j++) {
gray = *img_row;
uint8 min_cost = UINT8_MAX;
for (sint32 d = 0; d < disp_range; d+=step){
for (size_t k = 0; k < step; k++) {
cost_list[k] = cost_init_row[d + k];
l1_list[k] = cost_last_path[d + 1 + k];
l2_list[k] = cost_last_path[d + k] + P1;
l3_list[k] = cost_last_path[d + 2 + k] + P1;
l4_list[k] = mincost_last_path + std::max(P1, P2_Init / (abs(gray - gray_last) + 1));
}
mincost_last = simd256_set1(mincost_last_path);
cost = simd256_load((simd256type*)cost_list);
l1 = simd256_load((simd256type*)l1_list);
l2 = simd256_load((simd256type*)l2_list);
l3 = simd256_load((simd256type*)l3_list);
l4 = simd256_load((simd256type*)l4_list);
l1 = simd256_min(l1, l2);
l3 = simd256_min(l3, l4);
cost_s = simd256_min(l1, l3);
cost_s = simd256_add(cost, cost_s);
cost_s = simd256_sub(cost_s, mincost_last);
index = cost_aggr_row + d;
simd256_store((simd256type*)index, cost_s);
simd256_store((simd256type*)tmp, cost_s);
for (size_t k = 0; k < step; k++) {
min_cost = std::min(min_cost, tmp[k]);
}
}
// 重置上个像素的最小代价值和代价数组
mincost_last_path = min_cost;
memcpy(&cost_last_path[1], cost_aggr_row, disp_range * sizeof(uint8));
// 下一个像素
cost_init_row += direction * disp_range;
cost_aggr_row += direction * disp_range;
img_row += direction;
// 像素值重新赋值
gray_last = gray;
}
}
sgm_util::aligned_free<pixeltype>(cost_list);
sgm_util::aligned_free<pixeltype>(l1_list);
sgm_util::aligned_free<pixeltype>(l2_list);
sgm_util::aligned_free<pixeltype>(l3_list);
sgm_util::aligned_free<pixeltype>(l4_list);
sgm_util::aligned_free<pixeltype>(cost_s_list);
sgm_util::aligned_free<pixeltype>(tmp);
auto end = std::chrono::steady_clock::now();
auto tt = std::chrono::duration_cast<std::chrono::milliseconds>(end - start);
printf("sgm_util::CostAggregateLeftRight Done! Timing : %lf s\n\n", tt.count() / 1000.0);
}多线程优化
这里,我们主要用到C++的thread库和omp库进行多线程优化
同时计算8或者16个最小代价路径计算
std::vector<std::thread> threads;
if (option_.num_paths == 4 || option_.num_paths == 8) {
// 左右聚合
std::thread t1(sgm_util::CostAggregateLeftRight, img_left_, width_, height_, min_disparity, max_disparity, P1, P2_Int, cost_init_, cost_aggr_1_, true);
std::thread t2(sgm_util::CostAggregateLeftRight, img_left_, width_, height_, min_disparity, max_disparity, P1, P2_Int, cost_init_, cost_aggr_2_, false);
// 上下聚合
std::thread t3(sgm_util::CostAggregateUpDown, img_left_, width_, height_, min_disparity, max_disparity, P1, P2_Int, cost_init_, cost_aggr_3_, true);
std::thread t4(sgm_util::CostAggregateUpDown, img_left_, width_, height_, min_disparity, max_disparity, P1, P2_Int, cost_init_, cost_aggr_4_, false);
threads.push_back(std::move(t1));
threads.push_back(std::move(t2));
threads.push_back(std::move(t3));
threads.push_back(std::move(t4));
}
for (auto& thread : threads) {
thread.join();
}计算代价(基于Hamming距离)
采用omp的#pragma omp parallel for num_threads(2*omp_get_num_procs()-1)
直接把for循环中的线程数开到最大。
// 计算代价(基于Hamming距离)
#pragma omp parallel for num_threads(2*omp_get_num_procs()-1)
for (sint32 i = 0; i < height_; i++) {
for (sint32 j = 0; j < width_; j++) {
// 逐视差计算代价值
for (sint32 d = min_disparity; d < max_disparity; d++) {
auto& cost = cost_init_[i * width_ * disp_range + j * disp_range + (d - min_disparity)];
if (j - d < 0 || j - d >= width_) {
cost = UINT8_MAX/2;
continue;
}
if (option_.census_size == Census5x5) {
// 左影像census值
const auto& census_val_l = static_cast<uint32*>(census_left_)[i * width_ + j];
// 右影像对应像点的census值
const auto& census_val_r = static_cast<uint32*>(census_right_)[i * width_ + j - d];
// 计算匹配代价
cost = sgm_util::Hamming32(census_val_l, census_val_r);
}
else {
const auto& census_val_l = static_cast<uint64*>(census_left_)[i * width_ + j];
const auto& census_val_r = static_cast<uint64*>(census_right_)[i * width_ + j - d];
cost = sgm_util::Hamming64(census_val_l, census_val_r);
}
}
}
}最终,结合SIMD256和多线程优化,对于图像大小为1000 * 750,视差范围为64,计算时间由2.461s,下降为0.785,减少了68%左右。

版权声明:本文为博主JinSu_原创文章,版权归属原作者,如果侵权,请联系我们删除!
原文链接:https://blog.csdn.net/jin739738709/article/details/123048723
