【C++】单链表——单链表的基本操作

1、单链表的定义

由于顺序表的插入删除操作需要移动大量的元素，影响了运行效率，因此引入了线性表的链式存储——单链表。单链表通过一组任意的存储单元来存储线性表中的数据元素，不需要使用地址连续的存储单元，因此它不要求在逻辑上相邻的两个元素在物理位置上也相邻。

单链表的特点：

单链表不要求逻辑上相邻的两个元素在物理位置上也相邻，因此不需要连续的存储空间。
单链表是非随机的存储结构，即不能直接找到表中某个特定的结点。查找某个特定的结点时，需要从表头开始遍历，依次查找。

优点：

支持动态内存分配。由于单链表不需要预先分配一段连续的空间，因此可以根据实际需求动态地申请、释放节点空间，避免浪费内存。
支持高效的插入、删除操作。由于单链表中的节点是通过指针相连的，因此在插入、删除一个节点时，只需要修改其前驱节点或后继节点的指针即可，时间复杂度为O ( 1 ) 。

缺点：

不支持随机访问。由于单链表中的节点不是连续存储的，因此不能像数组一样通过下标来直接访问一个元素，需要从头节点开始遍历整个链表才能访问任意位置的元素。

创建一个类

template <class T>								// T为单链表存储的元素类型
class linkList
{
private:
    struct Node
    {
    public:
        T  data;								  // 结点的数据域 
        Node* next;								  // 结点的指针域，指向后继结点 
        Node(const T value, Node* p = NULL)       // 具有两个参数的Node构造函数 
        {	
            data = value;
            next = p;
        }
        Node(Node* p = NULL)                      // 具有一个参数的Node构造函数  
        { 						
            next = p;
        }
    };


    Node* head;								// 单链表的头指针 
    Node* tail;    							// 单链表的尾
    int curLength;							// 单链表的当前长度
    Node* getPosition(int i)const;			// 返回指向单链表中第i个元素的指针     

public:
    linkList();								    // 构造函数 
    ~linkList();								// 析构函数  
    void clear(); 								// 将单链表清空，使之成为空表
    bool empty()const;                          // 判空
    int size();                                 // 返回单链表的当前实际长度  						 
    void insert(int i, const T& value);	        // 在位置i上插入一个元素value，表的长度增1
    void remove(int i);							// 删除位置i上的元素value，若删除位置合法，表的长度减1 
    int search(const T& value)const;		    // 查找值为value的元素第一次出现的位序
    T visit(int i)const;					    // 访问位序为i的元素值，“位序”0表示第一个元素，类似于数组下标
    void traverse()const;						// 遍历单链表	
    void headCreate();							// “头插法”
    void tailCreate();							// “尾插法”
    void inverse();								// 逆置单链表
    int prior(const T& value)const;		        // 查找值为value的元素的前驱

};

2、单链表的初始化

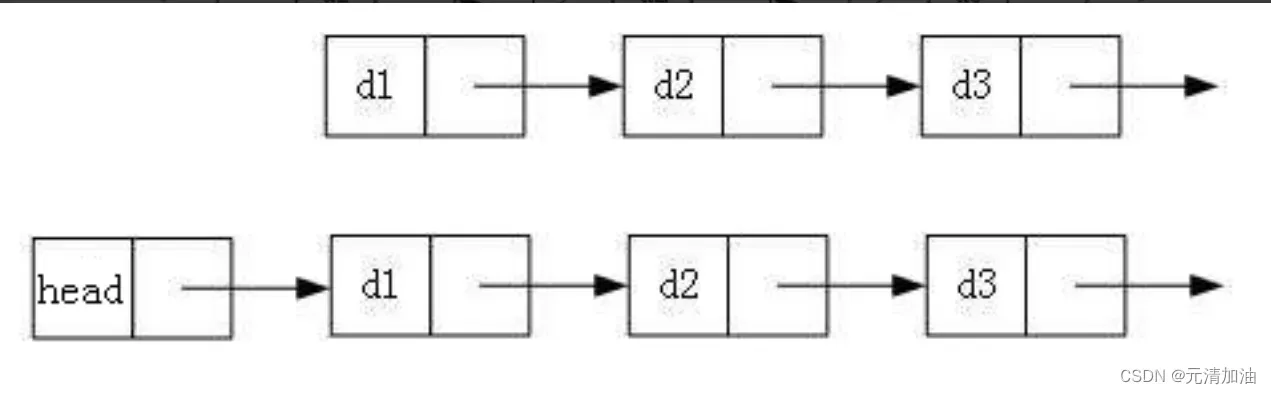
通常会用头指针来标识一个单链表，头指针为nullptr时表示一个空表。
但是，为了操作方便，会在单链表的第一个结点之前附加一个结点，称为头结点。
头结点的数据域可以不设任何信息，也可以记录表长等信息。

代码实现：

template <class T>
linkList<T>::linkList()
{
    head = tail = new Node();				    // 创建带有头结点的空表
    curLength = 0;
}

3、单链表的建立

3.1、头插法建立单链表

头插法建立单链表是说将新结点插入到当前链表的表头，即头结点之后。

思路：输入一个结束标志flag，使用一个while循环，判断条件是 value != flag

代码实现：

template <class T>  						// 头插法创建 
void linkList<T>::headCreate()
{
    Node* p;
    T value, flag;
    cin >> flag;									// 输入结束标志

    cin >> value;
    while (value != flag)
    {
        p = new Node(value);
        p->next = head->next;
        head->next = p;
        curLength++;
        cin >> value;
    }
}

3.2、尾插法建立单链表

尾插法建立单链表，就是将新结点插入到当前链表的表尾。

代码实现：

template <class T>  						// 尾插法创建链表
void linkList<T> ::tailCreate()
{
    Node* p;
    T value, flag;
    cin >> flag;									// 输入结束标志

    cin >> value;
    while (value != flag)
    {
        p = new Node(value);
        tail->next = p;
        tail = p;
        curLength++;
        cin >> value;
    }

}

4、单链表的遍历

代码实现：

template <class T>
void  linkList<T> ::traverse()const
{
    Node* p = head->next;
    while (p != nullptr)
    {
        cout << p->data << "  ";
        p = p->next;
    }
    cout << endl;
 
}

5、单链表的长度

代码实现：

template <class T>
int linkList<T>::size()
{ 
    return curLength; 
}

6、单链表的查找

6.1、按值查找

代码实现：

template <class T>
int linkList<T> ::search(const T& value)const
{
    Node* current = head->next;
    int i = 0;
    while (current != nullptr)
    {
        if (current->data == value)
        {
            break;
        }
        else
        {
            current = current->next;
            i++;
        }
    }
    if (current != nullptr)
    {
        return i;
    }
    return -1;


}

6.2、按位查找

代码实现：

template <class T>  						// 访问位序为i的元素返回其数据域
T linkList<T> ::visit(int i)const 
{

    if (i < 0 || i>(curLength - 1))
    {
        T a = 0;
        return a;
    }
    Node* current = head->next;
    while (i--)
    {
        current = current->next;
    }

    return current->data;
 
}

7、单链表的插入

返回指向单链表中第i个元素的指针

template <class T>
typename linkList<T> ::Node* linkList<T> ::getPosition(int i)const
{
    Node* ptemp = head;
    int k = 0;
    while (k < i)
    {
        ptemp = ptemp->next;
        k++;
    }
    return ptemp;
}

代码实现：

template  <class T>
void linkList<T> ::insert(int i, const T& value)
{
    Node* current = getPosition(i);
    Node* newNode = new Node(value);
    newNode->next = current->next;
    current->next = newNode;
    curLength++;

}

8、单链表的删除

代码实现：

template  <class T>
void  linkList<T>::remove(int i)
{

    Node* current = getPosition(i);
    Node* del = current->next;
    current->next = del->next;
    delete del;
    curLength--;
 
}

9、单链表的判空

代码实现：

template <class T>
bool linkList<T>::empty()const
{
    return head->next == nullptr;
}

总代码实现：

#include<stack>


template <class T>								// T为单链表存储的元素类型
class linkList
{
private:
    struct Node
    {
    public:
        T  data;								  // 结点的数据域 
        Node* next;								  // 结点的指针域，指向后继结点 
        Node(const T value, Node* p = NULL)       // 具有两个参数的Node构造函数 
        {	
            data = value;
            next = p;
        }
        Node(Node* p = NULL)                      // 具有一个参数的Node构造函数  
        { 						
            next = p;
        }
    };


    Node* head;								// 单链表的头指针 
    Node* tail;    							// 单链表的尾
    int curLength;							// 单链表的当前长度
    Node* getPosition(int i)const;			// 返回指向单链表中第i个元素的指针     

public:
    linkList();								    // 构造函数 
    ~linkList();								// 析构函数  
    void clear(); 								// 将单链表清空，使之成为空表
    bool empty()const;                          // 判空
    int size();                                 // 返回单链表的当前实际长度  						 
    void insert(int i, const T& value);	        // 在位置i上插入一个元素value，表的长度增1
    void remove(int i);							// 删除位置i上的元素value，若删除位置合法，表的长度减1 
    int search(const T& value)const;		    // 查找值为value的元素第一次出现的位序
    T visit(int i)const;					    // 访问位序为i的元素值，“位序”0表示第一个元素，类似于数组下标
    void traverse()const;						// 遍历单链表	
    void headCreate();							// “头插法”
    void tailCreate();							// “尾插法”
    void inverse();								// 逆置单链表
    int prior(const T& value)const;		        // 查找值为value的元素的前驱

};

template <class T>
linkList<T>::linkList()
{
    head = tail = new Node();				    // 创建带有头结点的空表
    curLength = 0;
}

template <class T>
linkList<T>::~linkList()
{
    clear();
    delete head;								// 删除头结点
}

template <class T>
bool linkList<T>::empty()const
{
    return head->next == nullptr;
}

template <class T>
int linkList<T>::size()
{ 
    return curLength; 
}

template <class T>
void linkList<T>::clear()
{

    Node* p = head->next;
    while (p)
    {
        head = head->next;
        delete p;
        p = head;
    }

}

template <class T>
typename linkList<T> ::Node* linkList<T> ::getPosition(int i)const
{
    Node* ptemp = head;
    int k = 0;
    while (k < i)
    {
        ptemp = ptemp->next;
        k++;
    }
    return ptemp;
}


template  <class T>
void linkList<T> ::insert(int i, const T& value)
{
    Node* current = getPosition(i);
    Node* newNode = new Node(value);
    newNode->next = current->next;
    current->next = newNode;
    curLength++;

}

template  <class T>
void  linkList<T>::remove(int i)
{

    Node* current = getPosition(i);
    Node* del = current->next;
    current->next = del->next;
    delete del;
    curLength--;
  

}

template <class T>
void  linkList<T> ::traverse()const
{
    Node* p = head->next;
    while (p != nullptr)
    {
        cout << p->data << "  ";
        p = p->next;
    }
    cout << endl;
 
}

template <class T>
int linkList<T> ::search(const T& value)const
{


    Node* current = head->next;
    int i = 0;
    while (current != nullptr)
    {
        if (current->data == value)
        {
            break;
        }
        else
        {
            current = current->next;
            i++;
        }
    }
    if (current != nullptr)
    {
        return i;
    }
    return -1;


}

template <class T>  						// 访问位序为i的元素返回其数据域
T linkList<T> ::visit(int i)const 
{

    if (i < 0 || i>(curLength - 1))
    {
        T a = 0;
        return a;
    }
    Node* current = head->next;
    while (i--)
    {
        current = current->next;
    }

    return current->data;
 
}

template <class T>  						// 头插法创建 
void linkList<T>::headCreate()
{
    Node* p;
    T value, flag;
    cin >> flag;									// 输入结束标志

    cin >> value;
    while (value != flag)
    {
        p = new Node(value);
        p->next = head->next;
        head->next = p;
        curLength++;
        cin >> value;
    }
}

 

template <class T>  						// 尾插法创建链表
void linkList<T> ::tailCreate()
{
    Node* p;
    T value, flag;
    cin >> flag;									// 输入结束标志

    cin >> value;
    while (value != flag)
    {
        p = new Node(value);
        tail->next = p;
        tail = p;
        curLength++;
        cin >> value;
    }

}
template <class T>  						// 头插法逆置   
void linkList<T> ::inverse()
{

    Node* temp = nullptr;
    Node* p = head->next;
    head->next = nullptr;
    while (p != nullptr)
    {
        temp = p;
        p = p->next;
        temp->next = head->next;
        head->next = temp;
    }

}

template <class T>
int linkList<T> ::prior(const T& value)const
{
    Node* current = head->next;
    int a = 0;
    Node* p = nullptr;
    while (current != nullptr)
    {
        if (current->data == value)
        {
            break;
        }
        else
        {
            current = current->next;
            a++;
        }
    }
    if (current != nullptr)
    {
        return a - 1;
    }
    return -1;

}

执行

#include<iostream>
using namespace std;


#include"SList.h"



int main()
{
	linkList<int>* lk1, * lk2;
	lk1 = new linkList<int>();
	lk2 = new linkList<int>();
	int i;
	int val;
	lk1->headCreate();          // 测试头插法创建单链表
	lk2->tailCreate();          // 测试尾插法创建单链表 
	lk1->traverse();           // 测试遍历
	lk2->traverse();           // 测试遍历
	
	cout << "查找值为2的位序：" << lk1->search(2) << endl;
	cout << "查找位序为2的值" << lk1->visit(2) << endl;
	cout << "长度：" << lk1->size();
	return 0;
}

执行结果

文章出处登录后可见！

已经登录？立即刷新

【C++】单链表——单链表的基本操作

1、单链表的定义

2、单链表的初始化

3、单链表的建立

3.1、头插法建立单链表

3.2、尾插法建立单链表

4、单链表的遍历

5、单链表的长度

6、单链表的查找

6.1、按值查找

6.2、按位查找

7、单链表的插入

8、单链表的删除

9、单链表的判空

总代码实现：

执行

执行结果

相关推荐