数据结构上机实验——图的实现（以无向邻接表为例）、图的深度优先搜索（DFS）、图的广度优先搜索（BFS）

Table of Contents

文章目录

数据结构上机实验
- 1.要求
- 2.图的实现（以无向邻接表为例）
- - 2.1创建图
  - - 2.1.1定义图的顶点、边及类定义
    - 2.1.2创建无向图和查找
    - 2.1.3插入边
    - 2.1.4打印函数
  - 2.2图的深度优先搜索（DFS）
  - 2.3图的广度优先搜索（BFS）
- 3.全部源码
- - 测试：
  - Graph.h
  - test.cpp

数据结构上机实验

1.要求

图采用邻接表存储结构，编程实现图的深度优先搜索和广度优先搜索算法。

2.图的实现（以无向邻接表为例）

2.1创建图

2.1.1定义图的顶点、边及类定义

我们定义一个邻接表类（ALGraph）。这里实现一些基础的数据结构。要注意结构体的嵌套。

Edge: 用于表示图中的边，包含两个顶点（tail和head）和一个权重cost。

ArcNode: 用于表示图中的有向边，包含一个目标顶点adjvex、一个权重info和一个指向下一个有向边的指针nextarc。

VNode: 用于表示图中的顶点，包含一个数据值data和一个指向第一条边的指针fistarc。

AdjGraph: 用于表示整个图，包含一个顶点数组表vertices（最大顶点数为MAXVex）、顶点数vexnum、边数arcnum和图的类型kind。

#define MAXVex 20 //最大的顶点数	
#define VElemType int

typedef enum {
	DG,    //有向图
	UDG,   //无向图
	DN,    //有向网
	UDN    //无向网
}GraphKind;

//定义边
typedef struct 
{
	VElemType tail;
	VElemType head;
	int cost;
}Edge;

//定义边节点
typedef struct ArcNode 
{
	int adjvex;	 //终点在数组表中的下表
	int info;	 //权值
	ArcNode* nextarc; //下一个边的地址
}ArcNode;

//定义表头节点
typedef struct
{
	VElemType data;	 
	ArcNode* fistarc; //储存第一条边的结点地址
}VNode;

//定义邻接表
typedef struct
{
	VNode vertices[MAXVex]; //储存MAXVex个VNode的数组表
	int vexnum;    //顶点数
	int arcnum;    //边数
	GraphKind kind;
}AdjGraph;

//定义邻接表类
class ALGraph
{
private:
	AdjGraph ag;
};

2.1.2创建无向图和查找

CreateGraph函数:

该函数首先使用输入参数n和m来初始化图的顶点数和边数。它通过循环读入每个顶点的数据，并初始化顶点数组表。每个顶点的数据值被初始化为输入的值，而第一条边的地址被初始化为NULL。 接着，它通过循环读入每条边的信息，并建立边集。对于每条边，它查找两个顶点的位置，然后创建一个新的ArcNode来存储这条边。如果图是无向的（kind == UDN），它还会创建另一个ArcNode来存储反向边。

LocateVex函数:

这个函数用于查找给定数据值在顶点数组表中的位置。 它遍历整个顶点数组表，如果找到匹配的数据值，就返回该位置的索引；否则，返回-1。

//创建无向图
void CreateGraph(int n, int m)
{
	ag.vexnum = n;  //ag有n个顶点
	ag.arcnum = m;  //ag有m个边

	ag.kind = UDN;
	int i, j, w, h, t;
	VElemType u, v;
	ArcNode* p;
	for (i = 0; i < n; i++)  //初始化顶点数组表
	{
		cin >> ag.vertices[i].data;
		ag.vertices[i].fistarc = NULL;
	}

	for (j = 0; j < m; j++) //建立边集
	{
		cin >> u >> v >> w;  //输入一条弧<u,v,w>
		h = LocateVex(u);
		t = LocateVex(v);
		p = new ArcNode;  //储存无向边
		p->adjvex = t;
		p->info = w;
		p->nextarc = ag.vertices[h].fistarc;
		if (ag.kind == UDN)  //储存无向边（v,u）
		{
			ag.vertices[h].fistarc = p;
			p = new ArcNode;
			p->adjvex = h;
			p->info = w;
			p->nextarc = ag.vertices[t].fistarc;
			ag.vertices[t].fistarc = p;
		}
	}
}

//查找顶点信息在数组中的下表
int LocateVex(VElemType u)
{
	for (int i = 0; i < ag.vexnum; i++)
	{
		if (u == ag.vertices[i].data)
		{
			return i;
		}
	}

	return -1;
}

2.1.3插入边

InsertArcGraph：

接受三个参数：顶点u、顶点v和边的权重info。代码实现了向图中插入新的边的功能。如果指定的两个顶点不存在，则会在顶点数组表中插入它们。 然后，创建两个新的ArcNode节点来代表双向边，并将它们插入到两个顶点的第一条边链表中。最后，更新图的状态信息（顶点数和边数）。

//插入边
void InsertArcGraph(VElemType u, VElemType v, int info)
{
	int h = LocateVex(u), t = LocateVex(v);
	ArcNode* p;
	if (h == -1)  //在顶点数组表中插入顶点u
	{
		ag.vertices[ag.vexnum].data = u;
		ag.vertices[ag.vexnum].fistarc = NULL;
		h = ag.vexnum;
		ag.vexnum++;
	}
	if (t == -1)  //在顶点数组表中插入顶点t
	{
		ag.vertices[ag.vexnum].data = v;
		ag.vertices[ag.vexnum].fistarc = NULL;
		t = ag.vexnum;
		ag.vexnum++;
	}
	p = new ArcNode;
	p->adjvex = t;
	p->info = info;
	p->nextarc = ag.vertices[h].fistarc;
	ag.vertices[h].fistarc = p;

	p = new ArcNode;
	p->adjvex = h;
	p->info = info;
	p->nextarc = ag.vertices[t].fistarc;
	ag.vertices[t].fistarc = p;
	ag.arcnum++;
}

2.1.4打印函数

Print()

这段代码是一个用于打印图的顶点和边信息的函数。 它遍历图的顶点数组表和邻接表，并打印每个顶点的索引、数据值和邻居信息。输出格式可以帮助理解图的结构和连接关系。

//打印函数
void Print()
{
	// 顶点
	for (size_t i = 0; i < ag.vexnum; ++i)
	{
		cout << "[" << i << "]" << "->" << ag.vertices[i].data << endl;
	}
	cout << endl;

	for (size_t i = 0; i < ag.vexnum; ++i)
	{
		cout << ag.vertices[i].data << "[" << i << "]->";
		ArcNode* cur = ag.vertices[i].fistarc;
		while (cur)
		{
			cout << "[" << cur->adjvex << ":" << cur->info << "]->";
			cur = cur->nextarc;
		}
		cout << "NULL" << endl;
	}

	cout << endl;
}

2.2图的深度优先搜索（DFS）

深度优先搜索（DFS）是一种用于遍历或搜索树或图的算法。这个算法会尽可能深地搜索图的分支。当节点v的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。

实现图的深度优先搜索（DFS）的算法。我们使用递归即可，同时要使用数组vis来追踪哪些节点已经被访问过。

在DFS函数中，我们应该使用节点的索引进行访问和标记，如果遇到了没有标记的点，就进行DFS操作，直到遍历完我们所有的图即可。

//深度优先搜索
int vis[MAXVex];
void DFS(VElemType v)
{
	ArcNode* p;
	int h = LocateVex(v);
	cout << v;
	vis[h] = 1;
	for (p = ag.vertices[h].fistarc; p; p = p->nextarc)
	{
		if (vis[p->adjvex] == 0)
		{
			DFS(ag.vertices[p->adjvex].data);
		}
	}
}
void DFSTraverse()
{
	int i;
	for (i = 0; i < ag.vexnum; i++)
	{
		vis[i] = 0;
	}
	for (i = 0; i < ag.vexnum; i++)
	{
		if (!vis[i])
		{
			DFS(ag.vertices[i].data);
		}
	}
	cout << endl;
}

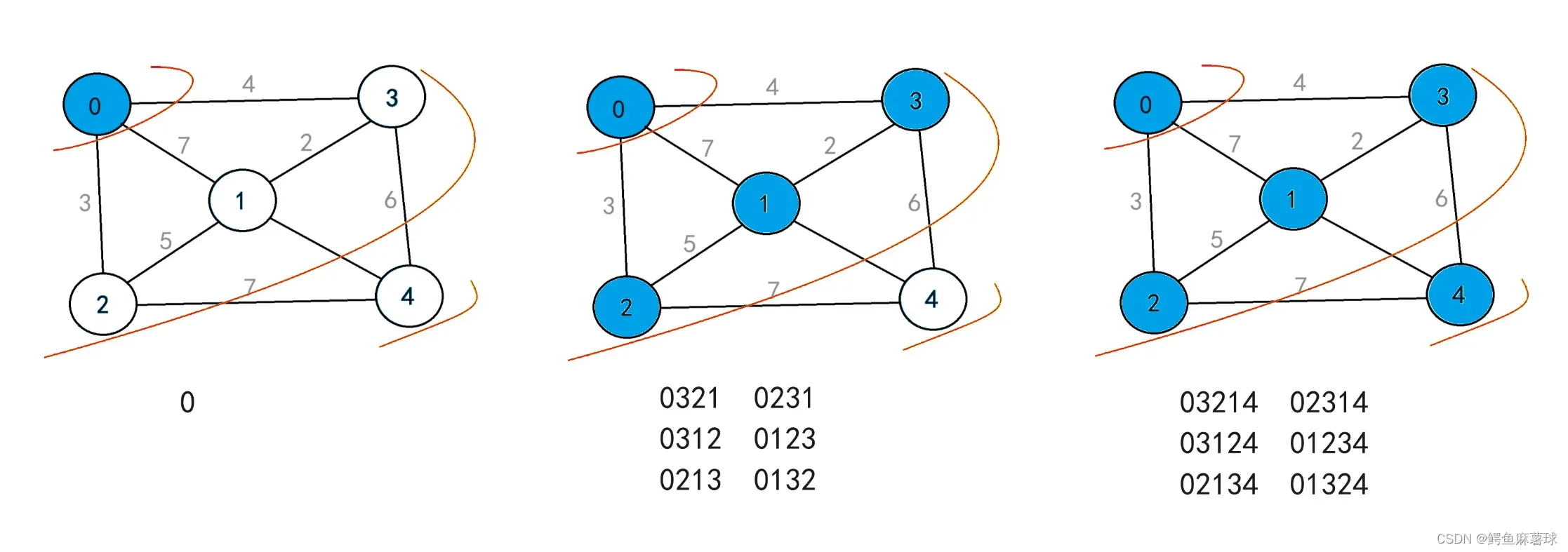
2.3图的广度优先搜索（BFS）

广度优先搜索（BFS）是一种用于图的遍历或搜索的算法。这种算法会尽可能广地搜索图的节点，从一个起始节点开始，探索邻近节点，然后再探索下一层级的节点。

图的广度优先搜索（BFS）算法，我们可以利用队列来实现，它是在图中查找从给定源节点到所有其他节点的路径的算法。在的代码中，我们需要定义了一个数组visi来跟踪已经访问过的节点，然后使用队列lq来存储待访问的节点。

在BFSTraverse函数中，我们先初始化visi数组，然后遍历所有的节点。如果一个节点尚未被访问，你就调用BFS函数进行访问。使用传递进来的节点数据来查找其在图中的索引，然后不断重复操作，知道队列中的数据为0。

//广度优先搜索
int visi[MAXVex];
void BFS(VElemType v)
{
	int h = LocateVex(v);
	ArcNode* p;
	queue<VElemType> lq;
	lq.push(h);
	visi[h] = 1;
	while (!lq.empty())
	{
		h=lq.front();
		lq.pop();
		cout << ag.vertices[h].data;
		for (p = ag.vertices[h].fistarc; p; p = p->nextarc)
		{
			if (!visi[p->adjvex])
			{
				lq.push(p->adjvex);
				visi[p->adjvex] = 1;
			}
		}
	}
}
void BFSTraverse()
{
	int i;
	for (i = 0; i < ag.vexnum; i++)
	{
		visi[i] = 0;
	}
	for (i = 0; i < ag.vexnum; i++)
	{
		if (!visi[i])
		{
			BFS(ag.vertices[i].data);
		}
	}
	cout << endl;
}

3.全部源码

测试：

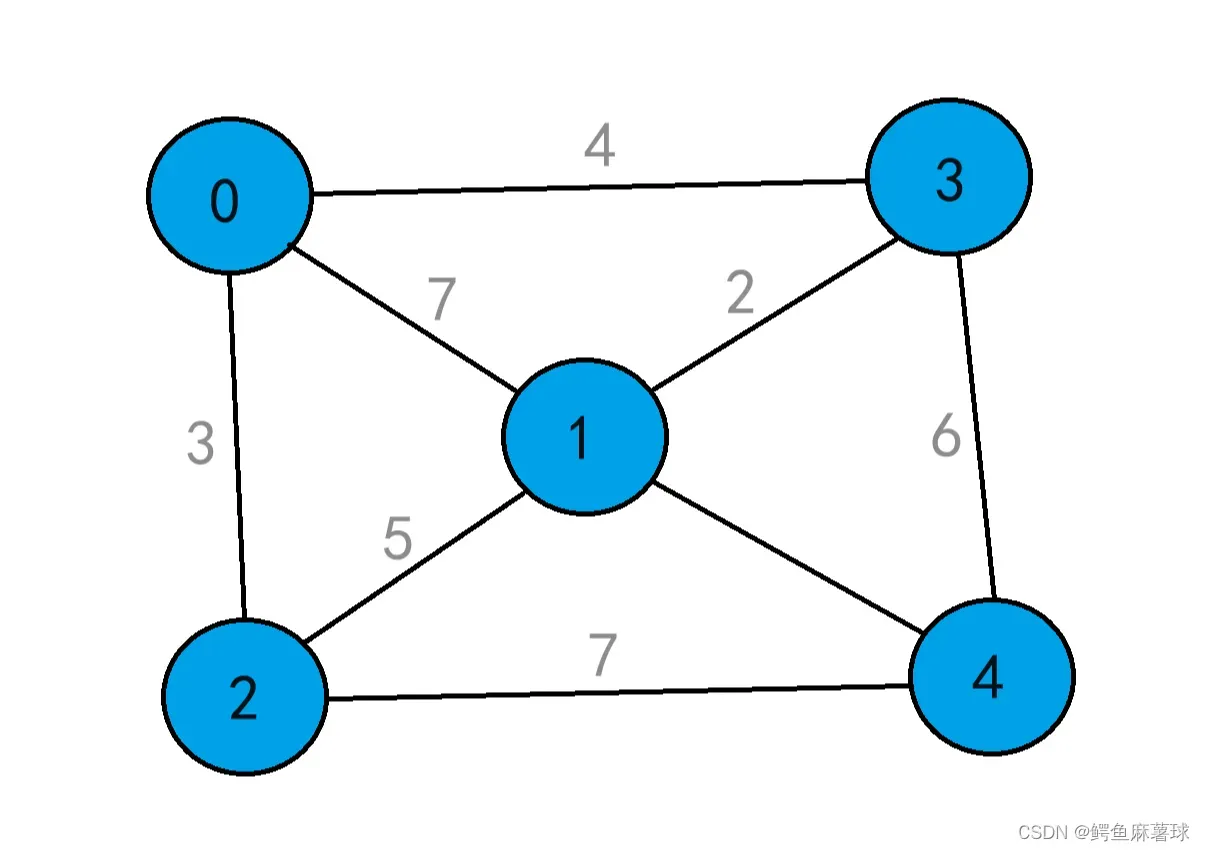
完全联通图示例：

有孤立点的示例：

Graph.h

#pragma once

#include<queue>

namespace link_table
{
#define MAXVex 20 //最大的顶点数	
#define VElemType int

typedef enum {
	DG,    //有向图
	UDG,   //无向图
	DN,    //有向网
	UDN    //无向网
}GraphKind;

//定义边
typedef struct 
{
	VElemType tail;
	VElemType head;
	int cost;
}Edge;

//定义边节点
typedef struct ArcNode 
{
	int adjvex;	 //终点在数组表中的下表
	int info;	 //权值
	ArcNode* nextarc; //下一个边的地址
}ArcNode;

//定义表头节点
typedef struct
{
	VElemType data;	 
	ArcNode* fistarc; //储存第一条边的结点地址
}VNode;

//定义邻接表
typedef struct
{
	VNode vertices[MAXVex]; //储存MAXVex个VNode的数组表
	int vexnum;    //顶点数
	int arcnum;    //边数
	GraphKind kind;
}AdjGraph;

//定义邻接表类
class ALGraph
{
public:
	//创建无向图
	void CreateGraph(int n, int m)
	{
		ag.vexnum = n;  //ag有n个顶点
		ag.arcnum = m;  //ag有m个边

		ag.kind = UDN;
		int i, j, w, h, t;
		VElemType u, v;
		ArcNode* p;
		for (i = 0; i < n; i++)  //初始化顶点数组表
		{
			cin >> ag.vertices[i].data;
			ag.vertices[i].fistarc = NULL;
		}

		for (j = 0; j < m; j++) //建立边集
		{
			cin >> u >> v >> w;  //输入一条弧<u,v,w>
			h = LocateVex(u);
			t = LocateVex(v);
			p = new ArcNode;  //储存无向边
			p->adjvex = t;
			p->info = w;
			p->nextarc = ag.vertices[h].fistarc;
			if (ag.kind == UDN)  //储存无向边（v,u）
			{
				ag.vertices[h].fistarc = p;
				p = new ArcNode;
				p->adjvex = h;
				p->info = w;
				p->nextarc = ag.vertices[t].fistarc;
				ag.vertices[t].fistarc = p;
			}
		}
	}

	//查找顶点信息在数组中的下表
	int LocateVex(VElemType u)
	{
		for (int i = 0; i < ag.vexnum; i++)
		{
			if (u == ag.vertices[i].data)
			{
				return i;
			}
		}

		return -1;
	}

	//计算顶点的度数
	int Degree(VElemType u)
	{
		int h = LocateVex(u);
		int count = 0;
		ArcNode* p = ag.vertices[h].fistarc;
		while (p)
		{
			count++;
			p = p->nextarc;
		}

		return count;
	}

	//插入边
	void InsertArcGraph(VElemType u, VElemType v, int info)
	{
		int h = LocateVex(u), t = LocateVex(v);
		ArcNode* p;
		if (h == -1)  //在顶点数组表中插入顶点u
		{
			ag.vertices[ag.vexnum].data = u;
			ag.vertices[ag.vexnum].fistarc = NULL;
			h = ag.vexnum;
			ag.vexnum++;
		}
		if (v == INT32_MAX) return;
		if (t == -1)  //在顶点数组表中插入顶点t
		{
			ag.vertices[ag.vexnum].data = v;
			ag.vertices[ag.vexnum].fistarc = NULL;
			t = ag.vexnum;
			ag.vexnum++;
		}
		p = new ArcNode;
		p->adjvex = t;
		p->info = info;
		p->nextarc = ag.vertices[h].fistarc;
		ag.vertices[h].fistarc = p;

		p = new ArcNode;
		p->adjvex = h;
		p->info = info;
		p->nextarc = ag.vertices[t].fistarc;
		ag.vertices[t].fistarc = p;
		ag.arcnum++;
	}

	//深度优先搜索
	int vis[MAXVex];
	void DFS(VElemType v)
	{
		ArcNode* p;
		int h = LocateVex(v);
		cout << v;
		vis[h] = 1;
		for (p = ag.vertices[h].fistarc; p; p = p->nextarc)
		{
			if (vis[p->adjvex] == 0)
			{
				DFS(ag.vertices[p->adjvex].data);
			}
		}
	}
	void DFSTraverse()
	{
		int i;
		for (i = 0; i < ag.vexnum; i++)
		{
			vis[i] = 0;
		}
		for (i = 0; i < ag.vexnum; i++)
		{
			if (!vis[i])
			{
				DFS(ag.vertices[i].data);
			}
		}
		cout << endl;
	}

	//广度优先搜索
	int visi[MAXVex];
	void BFS(VElemType v)
	{
		int h = LocateVex(v);
		ArcNode* p;
		queue<VElemType> lq;
		lq.push(h);
		visi[h] = 1;
		while (!lq.empty())
		{
			h=lq.front();
			lq.pop();
			cout << ag.vertices[h].data;
			for (p = ag.vertices[h].fistarc; p; p = p->nextarc)
			{
				if (!visi[p->adjvex])
				{
					lq.push(p->adjvex);
					visi[p->adjvex] = 1;
				}
			}
		}
	}
	void BFSTraverse()
	{
		int i;
		for (i = 0; i < ag.vexnum; i++)
		{
			visi[i] = 0;
		}
		for (i = 0; i < ag.vexnum; i++)
		{
			if (!visi[i])
			{
				BFS(ag.vertices[i].data);
			}
		}
		cout << endl;
	}

	//打印函数
	void Print()
	{
		// 顶点
		for (size_t i = 0; i < ag.vexnum; ++i)
		{
			cout << "[" << i << "]" << "->" << ag.vertices[i].data << endl;
		}
		cout << endl;

		for (size_t i = 0; i < ag.vexnum; ++i)
		{
			cout << ag.vertices[i].data << "[" << i << "]->";
			ArcNode* cur = ag.vertices[i].fistarc;
			while (cur)
			{
				cout << "[" << cur->adjvex << ":" << cur->info << "]->";
				cur = cur->nextarc;
			}
			cout << "NULL" << endl;
		}

		cout << endl;
	}

private:
	AdjGraph ag;
};

}

test.cpp

#define _CRT_SECURE_NO_WARNINGS 1

#include<iostream>
using namespace std;

#include"Graph.h"

void TestGraph1()
{
	link_table::ALGraph ag;
	ag.CreateGraph(0, 0);
	ag.InsertArcGraph(0, 1, 7);
	ag.InsertArcGraph(0, 2, 3);
	ag.InsertArcGraph(0, 3, 4);
	ag.InsertArcGraph(3, 4, 6);
	ag.InsertArcGraph(1, 2, 5);
	ag.InsertArcGraph(1, 3, 2);
	ag.InsertArcGraph(1, 4, 1);
	ag.InsertArcGraph(2, 4, 7);
	//创建孤立点，INT32_MAX代表没有连接任何边
	ag.InsertArcGraph(5, INT32_MAX, 0);

	cout << "该相邻表为:\n";
	ag.Print(); 
	cout << "深度优先搜索的结果为:";
	ag.DFSTraverse();
	cout << "广度优先搜索的结果为:";
	ag.BFSTraverse();

}

int main()
{
	TestGraph1();
	return 0;
}

文章出处登录后可见！

已经登录？立即刷新