数据结构——哈夫曼树与哈夫曼编码

1. 哈夫曼树

1.1 基本概念

路径：指从根结点到该结点的分支序列。
路径长度：指根结点到该结点所经过的分支数目。
结点的带权路径长度：从树根到某一结点的路径长度与该结点的权的乘积。
树的带权路径长度(WPL)：树中从根到所有叶子结点的各个带权路径长度之和。

哈夫曼树是由 n 个带权叶子结点构成的所有二叉树中带权路径长度最短的二叉树，又称最优二叉树。如上图中第三棵树就是一棵哈夫曼树。

1.2 构造哈夫曼树
构造哈夫曼树的算法步骤：
① 初始化：用给定的 n 个权值{w1,w2,…,wn}构造 n 棵二叉树并构成的森林F={T1,T2,…,Tn}，其中每一棵二叉树Ti（1<=i<=n）都只有一个权值为 wi 的根结点，其左、右子树为空。
② 找最小树：在森林 F 中选择两棵根结点权值最小的二叉树，作为一棵新二叉树的左、右子树，标记新二叉树的根结点权值为其左、右子树的根结点权值之和。
③ 删除与加入：从 F 中删除被选中的那两棵二叉树，同时把新构成的二叉树加入到森林 F 中。
④ 判断：重复②、③操作，直到森林中只含有一棵二叉树为止，此时得到的这棵二叉树就是哈夫曼树。
简单的说就是先选择权小的，所以权小的结点被放置在树的较深层，而权较大的离根较近，这样一来所构成的哈夫曼树就具有最小带权路径长度。

2. 哈夫曼编码实现
2.1 哈夫曼编码
对一棵具有n个叶子结点的哈夫曼树，若对树中的每个左分支赋0，右分支赋1（或左1右0），则从根到每个叶子的通路上，各个分支的赋值分别构成一个二进制串，该二进制串就称为哈夫曼编码。哈夫曼编码是最优前缀编码，能使各种报文对应的二进制串的平均长度最短。
代码如下：

#include<stdio.h>
#include<string.h>
#include<malloc.h>
typedef struct hnode
{ int weight;
   int lchild,rchild,parent;
 }HTNode,*HuffmanTree;/*定义二叉树的存储结点*/
typedef char **HuffmanCode;
void Select(HTNode HT[],int len,int &s1,int &s2)//选出权值最小的两个结点，下标通过s1和s2传出去
{
    int i,min1=32767,min2=32767;
    for(i=1;i<=len;i++)
    {
        if(HT[i].weight<min1&&HT[i].parent==0)
        {
            s2=s1;
            min2=min1;
            min1=HT[i].weight;
            s1=i;
        }
        else if(HT[i].weight<min2&&HT[i].parent==0)
        {    min2=HT[i].weight;
            s2=i;
        }
    }
}
void CreateHuffman_tree(HuffmanTree &HT,int n)/*建立哈夫曼树*/
{
	int s1, s2;
	if(n <= 1)
	{ 
		return ;
	}
	int m = 2*n - 1;
	HT = new HTNode[m + 1];
	int i = 0;
	for(i = 1; i <= m; i++)
	{
		HT[i].parent = 0;
		HT[i].lchild = HT[i].rchild = 0; 
	}
	printf("哈夫曼树各节点的值：");
	for(i = 1; i <= n; i++)
	{
		scanf("%d", &HT[i].weight);
	}
	for(i = n + 1; i <=m; i++ )
	{
		Select(HT, i-1, s1, s2);
		HT[s1].parent = HT[s2].parent = i;
		HT[i].lchild = s1;
		HT[i].rchild = s2;
		HT[i].weight = HT[s1].weight + HT[s2].weight;
	}
}

void Huffman_code(HuffmanTree HT,HuffmanCode &HC,int n)/*哈夫曼树编码*/
{
	char *cd;
	int start = 0;
	int c = 0, f = 0, i = 0;
	HC = new char*[n + 1];
	cd = new char[n];
	cd[n-1] = '\0';
	for(i = 1; i <= n; ++i)
	{
		start = n - 1;
		c = i;
		f = HT[i].parent;
		while(f!= 0)
		{
			--start;
			if(HT[f].lchild == c)
			{
				cd[start] = '0';
			} 
			else
			{
				cd[start] = '1';
			}
            c = f;
            f = HT[f].parent;
			
		}
		HC[i] = new char[n-start];
			strcpy(HC[i], &cd[start]);
		
	}
	delete cd;
}


int main()
{
    HuffmanTree HT;
    HuffmanCode HC;
    int i, n;
    printf("哈夫曼树节点个数：");
    scanf("%d",&n);
    CreateHuffman_tree(HT, n);/*建立哈夫曼树*/
    Huffman_code(HT,HC,n);/*哈夫曼树编码*/
    for(i=1;i<=n;i++)/*输出字符、权值及编码*/
       printf("编码是：%s\n",HC[i]);
    return 0;
}

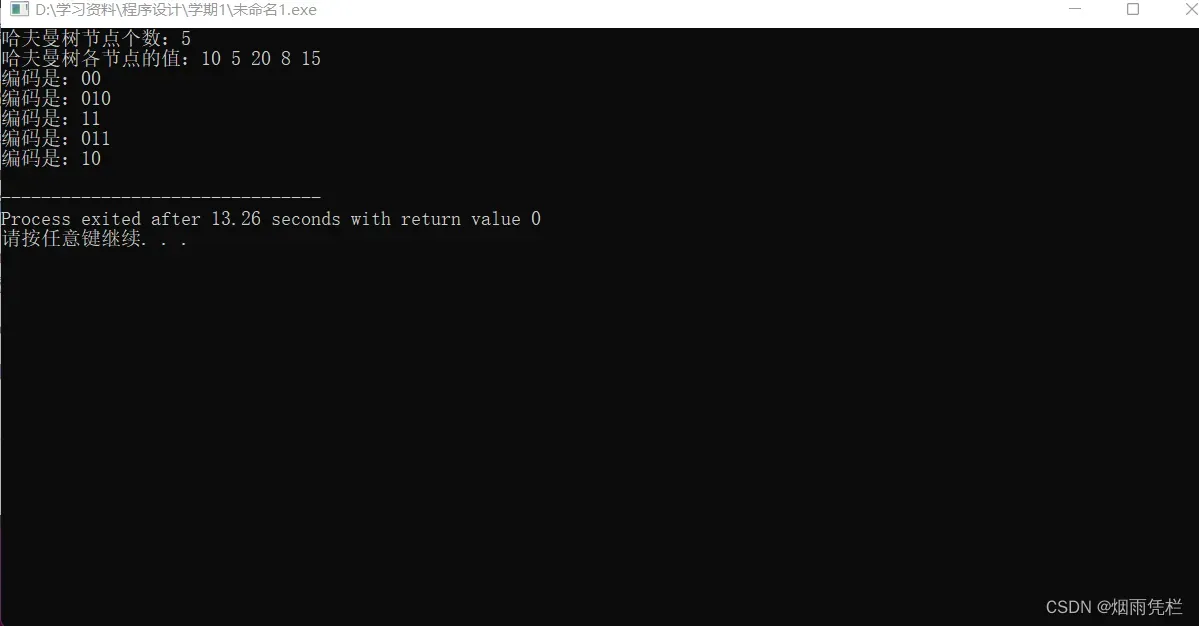
结果如下：