目录
一、分析
(一)定义问题的解空间
- 问题的解是从n个物品中选择一些物品使其在不超过容量的情况下价值最大。每个物品有且只有两种状态,要么装入背包,要不不装入。那么第i个物品装入背包,能够达到目标要求,还是不装入背包能够达到目标要求呢?很显然,目前还不确定。因此,可以用变量xi表示第i种物品是否被装入背包的行为,如果用“0”表示不被装入背包,用“1”表示装入背包,则xi的取值为0或1。
- 问题的解空间是{x1,x2,….x1,…xn},显约束是xi=0或1
(二)确定解空间的组织结构
问题的解空间描述了2ⁿ 种可能解,也可以说是n个元素组成的集合所有子集个数。例如3个物品的背包问题,解空间是:{0,0,0},{0,0,1},{0,1,0},{0,1,1},{1,0,0},{1,0,1},{1,1,0},{1,1,1}。该问题有2³个可能解。可见,问题的解空间树为子集树,解空间树的深度为问题的规模n
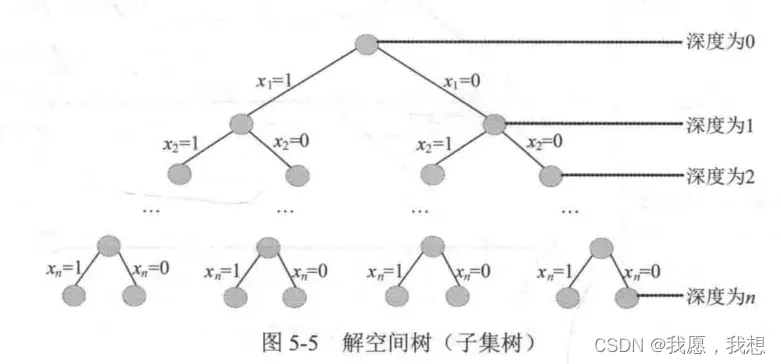
(三)搜索解空间
1. 约束条件
解空间包含2ⁿ种可能解,存在某种或某些物品无法装入的情况,因此需要设置约束条件,判断装入背包的物品总重量是否超出背包容量,如果超出,为不可行解;否则为可行解。搜索过程不再搜索那些导致不可行解的结点及其孩子结点。
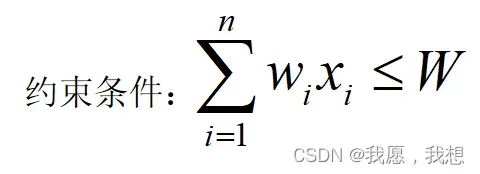
2. 限界条件
- 背包问题的可行解可能不止一个,问题的目标是找一个装入背包的物品总价值最大的可行解,即最优解。因此,需要设置限界条件来加速找出该最优解的速度。根据解空间的组织结构,对于任何一个中间结点z(中间状态),从根结点到z结点的分支所代表的状态(是否装入购物车)已经确定,从z到其子孙结点的分支的状态是不确定的。
- 也就是说,如果z在解空间树中所处的层次是t,说明第1种物品到第t-1种物品的状态已经确定了。我们只需要沿着z的分支扩展很容易确定第t种物品的状态。那么前t种物品的状态就确定了。但第t+1种物品到第n种物品的状态还不确定。这样,前t种物品的状态确定后,当前已装入背包的物品的总价值,用cp表示。已装入物品的价值高不一定就是最优的,因此还有剩余物品未确定。
- 我们还不确定第t+1种物品到第n种物品的实际状态,因此只能用估计值。假设第t+1种物品到第n种物品都装入背包,第t+1种物品到第n种物品的总价值用rp来表示,因此cp+rp是所有从根出发经过中间结点z的可行解的价值上界

(四)搜索过程
- 从根结点开始,以深度优先的方式进行搜索。根节点首先成为活结点,也是当前的扩展结点。由于子集树中约定左分支上的值为“1”,因此沿着扩展结点的左分支扩展,则代表装入物品。
- 此时,需要判断是否能够装入该物品,即判断约束条件成立与否,如果成立,即生成左孩子结点,左孩子结点成为活结点,并且成为当前的扩展结点,继续向纵深结点扩展;如果不成立,则剪掉扩展结点的左分支,沿着其右分支扩展,右分支代表物品不装入购物车,肯定有可能导致可行解。
- 但是沿着右分支扩展有没有可能得到最优解呢?这一点需要由限界条件来判断。如果限界条件满足,说明有可能导致最优解,即生成右孩子结点,右孩子结点成为活结点,并成为当前的扩展结点,继续向纵深结点扩展;如果不满足限界条件,则剪掉扩展结点的右分支,向最近的祖宗活结点回溯。搜索过程直到所有活结点变成死结点结束。
二、举例

三、核心代码
double Bound(struct goods* ps, int i)//计算上界(即当前价值和剩余物品总价值)
{
double sum = 0.0;//用于保存剩余物品价值
while (i < n)
{
sum += ps[i].v;
i++;
}
return sum+cv;
}void Backtrack(struct goods* ps, int i)//回溯
{
if (i >n-1)//已经到达了叶子结点(结束条件)
{
for (int k = 0; k < n; k++)
{
bestx[k] = ps[k].x;
}
bestv = cv;
return;
}
if (cw + ps[i].w <= bagW)//满足条件,扩展左分支
{
ps[i].x = true;//当前物品放入背包
cw += ps[i].w;//更新当前背包总重量
cv += ps[i].v;//更新当前背包总价值
Backtrack(ps, i + 1);
ps[i].x = false;//回溯
cw -= ps[i].w;//更新当前背包总重量
cv -= ps[i].v;//更新当前背包总价值
}
if (Bound(ps, i + 1) > bestv)//满足条件,扩展右分支
{
ps[i].x = false;
Backtrack(ps, i + 1);
}
}四、完整代码
#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
#define MAX 20//物品最多数量
struct goods
{
double w;//物品重量
double v;//物品价值
bool x;//物品是否放入背包
}g[MAX];
int n , bagW ;//物品数量和背包容量
double cw ;//当前放入背包的重量
double cv ;//当前放入背包的总价值
double bestv ;//当前最优价值
bool bestx[MAX];//当前最优解集合
//初始化物品信息
void Init( struct goods* ps, int n);
//限界函数
double Bound(struct goods* ps, int i);
//回溯
void Backtrack(struct goods* ps, int i);
//
void Knapsack(struct goods* ps, int _bagW);
void Init(struct goods* ps,int n)//初始化物品信息
{
cout << "请依次输入物品的重量和价值:\n";
for (int i = 0; i < n; i++)
{
cin >> ps[i].w >> ps[i].v;
ps[i].x = false;
}
}
double Bound(struct goods* ps, int i)//计算上界(即当前价值和剩余物品总价值)
{
double sum = 0.0;//用于保存剩余物品价值
while (i < n)
{
sum += ps[i].v;
i++;
}
return sum+cv;
}
void Backtrack(struct goods* ps, int i)//回溯
{
if (i >n-1)//已经到达了叶子结点(结束条件)
{
for (int k = 0; k < n; k++)
{
bestx[k] = ps[k].x;
}
bestv = cv;
return;
}
if (cw + ps[i].w <= bagW)//满足条件,扩展左分支
{
ps[i].x = true;//当前物品放入背包
cw += ps[i].w;//更新当前背包总重量
cv += ps[i].v;//更新当前背包总价值
Backtrack(ps, i + 1);
ps[i].x = false;//回溯
cw -= ps[i].w;//更新当前背包总重量
cv -= ps[i].v;//更新当前背包总价值
}
if (Bound(ps, i + 1) > bestv)//满足条件,扩展右分支
{
ps[i].x = false;
Backtrack(ps, i + 1);
}
}
void Knapsack(struct goods* ps,int _bagW)
{
//初始化
cw = 0.0;//当前放入背包的重量
cv = 0.0;//当前放入背包的总价值
bestv = 0.0;//当前最优价值
double sw = 0.0;//保存所有物品总重量
double sv = 0.0;//保存物品总价值
for (int i = 0; i < n; i++)
{
sw += ps[i].w;
sv += ps[i].v;
}
if (sw <= bagW)//意味着所有物品都可以装入
{
cout << "所有物品都可以放入购物车,且放入的总价值为:" << sv << endl;
return;
}
Backtrack(ps, 0);
cout << "放入背包的物品序号为:\n";
for (int k = 0; k < n; k++)
{
if (bestx[k] == true)
cout << k << " ";
}
cout << endl;
cout << "放入的总价值为:" << bestv << endl;
}
int main()
{
cout << "请分别输入物品的数量和背包总重量:\n";
cin >> n >> bagW;
Init(g, n);//初始化
Knapsack(g, bagW);
return 0;
}
//请分别输入物品的数量和背包总重量:
//4 10
//请依次输入物品的重量和价值:
//2 6
//5 3
//4 5
//2 4
//放入背包的物品序号为:
//0 2 3
//放入的总价值为:15文章出处登录后可见!
已经登录?立即刷新
