一、定义
随机森林是一种有监督学习算法,是以决策树为基学习器的集成学习算法。
那什么是有监督学习呢?有监督学习就是把有已知结果的数据集拿去训练,如果训练结果与标准答案的精度足够高就可以使用这个模型去预测或者分类未知结果的数据集。简单来说就是你写很多有标准答案的试卷,当你的准确率足够高的时候你就可以去写没有标准答案的试卷了,因为如果你平时都能考全国前三,那你高考就大概率能考到全国前三。有监督学习主要应用于分类和回归。
无监督学习的数据是没有已知结果的数据,比如清北大学自主招生考试,学校事先不知道学生平时的考试结果,但是有学生奥数经历的介绍,根据以往经验奥数高的一般考的就好,就收了,但是不排除奥数好但是成绩不行的学生存在。无监督学习主要用于聚类和降维。
集成学习故名思义就是“组合学习”,比如本文介绍的随机森林算法就是由很多个决策树组成的算法,假设有A、B两个选择,100个决策树一起投票,超过50个树投给了A那么随机森林的结果就是A。
二、模型理论
传统的决策树模型在训练时经常会出现过拟合的情况,随机森林是有效解决该问题的方法之一。随机森林本质上是很多树的组合,并且每一棵树因为取的样本略有不同所以树与树之间也是有所区别的。
随机森林的思想是每棵树的预测效果可能都相对较好但可能对部分数据过拟合,如果构造足够多的树,并且每棵树都可能有很好的预测结果但是也都会对不同的部分数据过拟合,我们可以通过取平均值来降低过拟合同时保证模型精度,这在数学上是被证明过的。
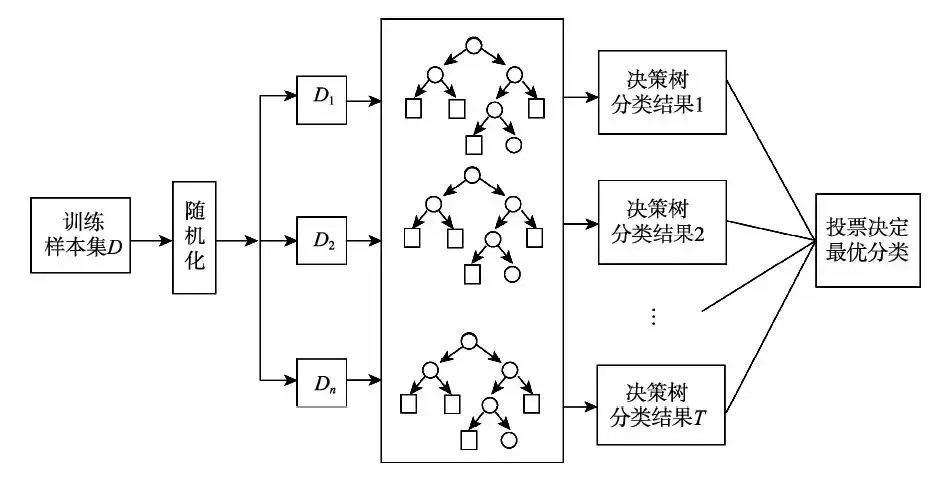
随机森林的随机性体现在两个方面,一个是特征随机性,一个是样本随机性。先随机抽取足够的样本,再根据这批样本选择最好的特征,这样每棵树的特征实际上都有可能不完全一样。因为随机性,森林的偏向可能会略有增加,但是因为取平均,它的方差也会减小,从而生成一个更好的模型。
算法过程如下:
(1)、通过有放回抽样的方法随机抽取n个样本作为决策树模型的样本
(2)、假设这些样本有M个特征,随机选择m个特征作为该决策树的分裂属性
(3)、重复(1)(2)n次就会生成n个决策树,这样就构成了随机森林,这些决策树的投票结果就是随机森林的结果。
三、优缺点
优点:
(1)、可以处理很高维度(特征很多)的数据,并且不用降维,不用做做特征选择
(2)、对数据集的适应能力强,既适用于离散型也适用于连续型数据
(3)、它可以判断特征的重要程度,筛选出重要特征,并且筛选结果也可以用于其他模型,是非常流行的特征筛选方法
(4)、由于采用集成算法,精度往往比单个模型的精度高
(5)、实现简单、精度高,不容易过拟合,可以作为基准模型
缺点:
(1)、随机森林已经被证明在某些噪音较大的分类或回归问题上会过拟合
(2)、对于有不同取值的属性的数据,取值划分较多的属性会对随机森林产生更大的影响,所以随机森林在这种数据上产出的属性权值是不可信的
四、参数介绍
n_estimators :树的数量,默认是10,就是你准备在你的森林里种多少树。这个参数是最重要的,树的数量决定了最后的准确性,但是也会让你的运行速度变的很慢,所以需要不断的测试去决定。
max_features:随机森林允许单个决策树使用特征的最大数量。
Auto/None/sqrt :简单地选取所有特征,每颗树都可以利用他们。这种情况下,每颗树都没有任何的限制。默认是auto
int:是整数
float:百分比选取
log2:所有特征数的log2值
criterion : criterion:分裂节点所用的标准,可选“gini”, “entropy”,默认“gini”。
max_depth:树的最大深度。如果为None,则将节点展开,直到所有叶子都是纯净的(只有一个类),或者直到所有叶子都包含少于min_samples_split个样本。默认是None
min_samples_split:拆分内部节点所需的最少样本数:如果为int,则将min_samples_split视为最小值。如果为float,则min_samples_split是一个分数,而ceil(min_samples_split * n_samples)是每个拆分的最小样本数。默认是2
min_samples_leaf:在叶节点处需要的最小样本数。仅在任何深度的分割点在左分支和右分支中的每个分支上至少留下min_samples_leaf个训练样本时,才考虑。这可能具有平滑模型的效果,尤其是在回归中。如果为int,则将min_samples_leaf视为最小值。如果为float,则min_samples_leaf是分数,而ceil(min_samples_leaf * n_samples)是每个节点的最小样本数。默认是1。
最主要的两个参数是n_estimators和max_features,n_estimators理论上是越大越好,但是计算时间也相应增长,所以预测效果最好的值将会出现在合理的树个数;max_features每个决策树在随机选择的特征里找到某个“最佳”特征,使得模型在该特征的某个值上分裂之后得到的收益最大化。max_features越少,方差就会减少,但同时偏差就会增加。如果是回归问题则max_features=n_features,如果是分类问题,则max_features=sqrt(n_features),其中,n_features 是输入特征数。
从下图中我们可以看到参数对Random Forest的影响: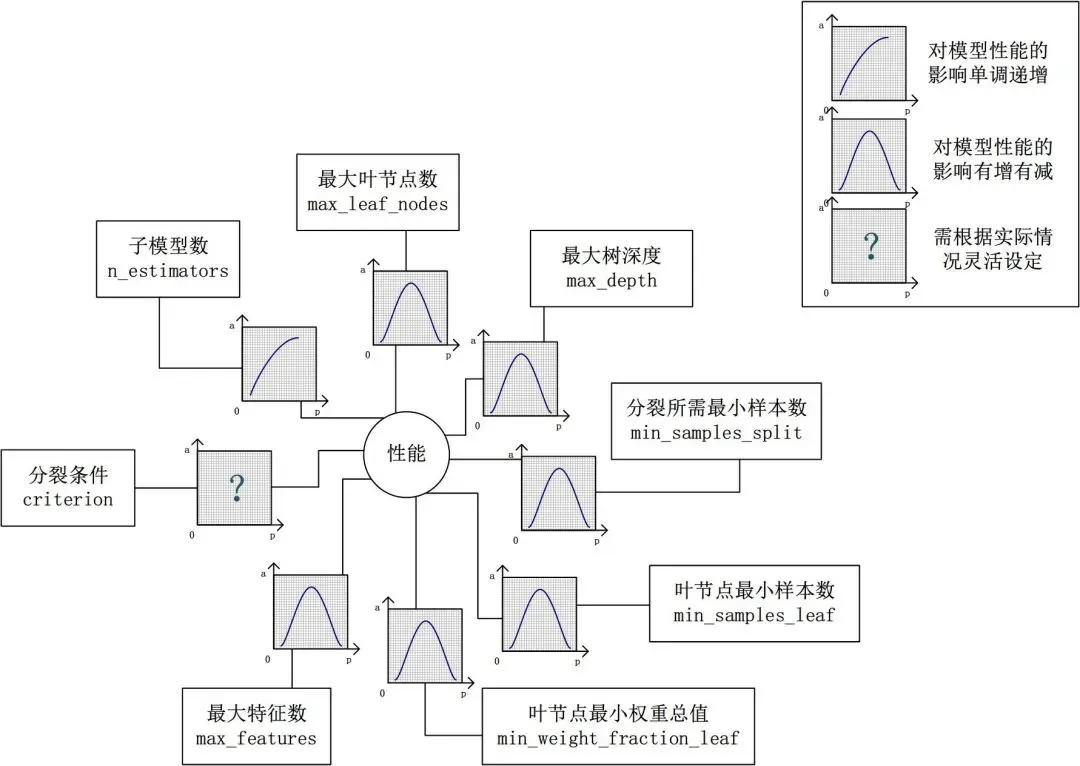
可以看到除了n_estimators外其余参数理论上都不是越大越好,包括 n_estimators实际中也不是越大越好,那如何调节出好的参数呢,一个一个试是不可能的,机器学习库提供了一个暴力调参的函数GridSearchCV(网格搜索),但是这个函数很容易让你的电脑爆炸,因为如果4个参数一起调,每个参数都是100种可能,那就会运行100x100x100x100次模型,显然这是不行的,但是我们可以通过贪心算法,即把最重要的两个参数放到GridSearchCV里找到最优参数,再把次要的参数放进去遍历。总之,不断的尝试就对了。
五、案例数据简介
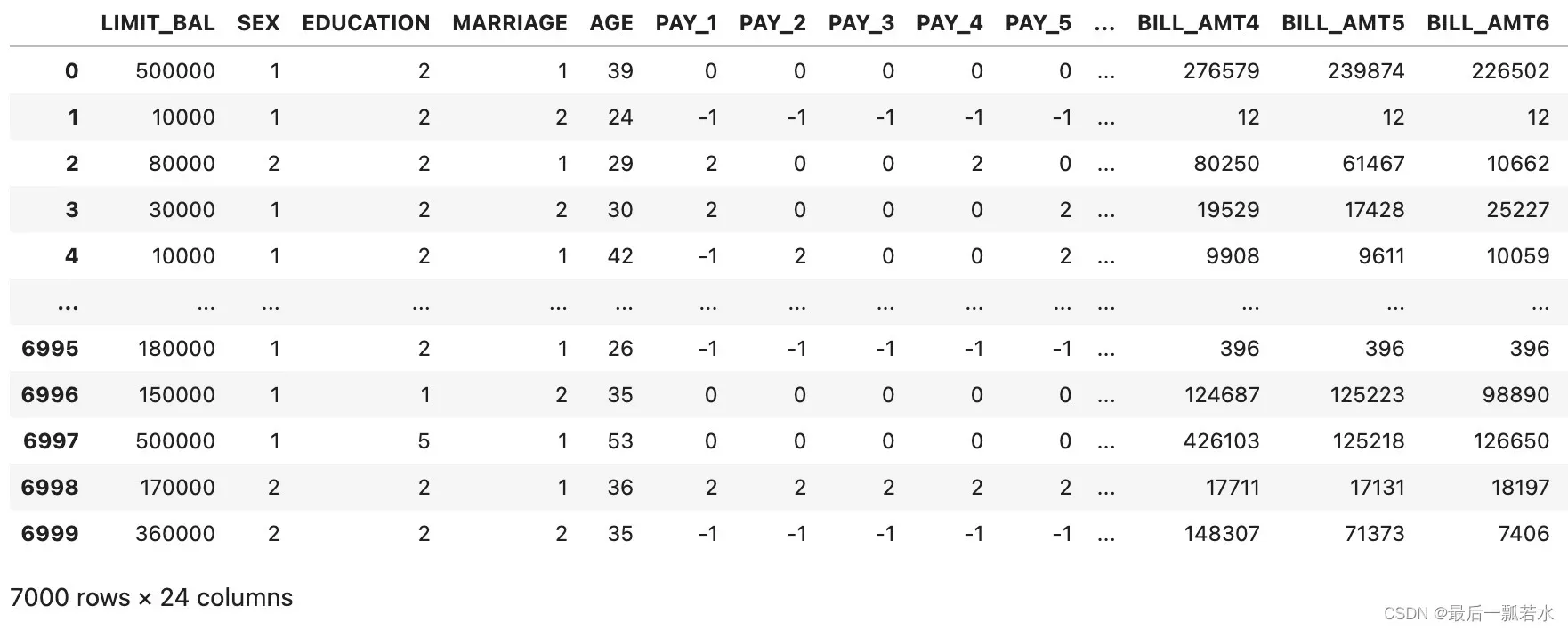
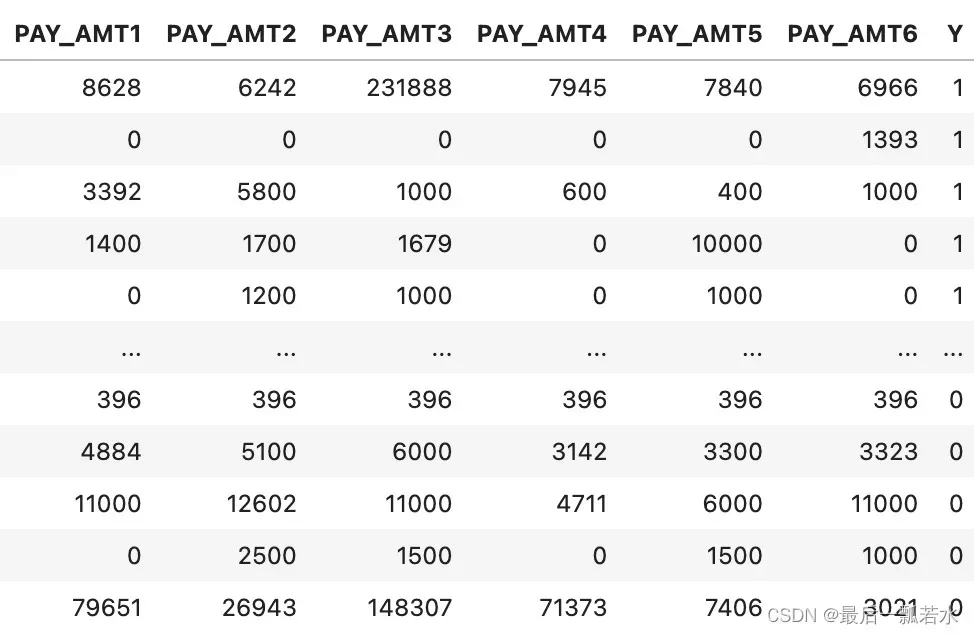
数据集中共有24个特征,7000个样本,从Y的值为0和1可以知道是二分类问题。这是比赛数据,非保密数据,只是我不知道怎么打包上传,如果有需要可以私信我。
六、案例建模及具体步骤
读取数据
import pandas as pd
datas=pd.read_csv('data_20221030(1).csv')
datas=datas[datas.columns[2:]]
datas数据如上面的截图所示👆
计算皮尔逊相关系数
plt.figure(figsize=(20,20))
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
sns.heatmap(discreat_data.corr(),cmap="YlGnBu",annot=True)
plt.title("相关性分析图")
想关性分析可以初步筛掉一些与Y相关性很低的特征,此处的皮尔逊相关系数其实适用于连续型数据,离散型数据用肯达尔相关系数和斯皮尔曼相关系数会更好一点。
这里仅演示没有筛指标也没有用其他两个相关系数,相关系数的介绍可以参考这里:
- (59条消息) 相关性分析、相关系数矩阵热力图_最后一瓢若水的博客-CSDN博客_相关系数矩阵热力图
划分训练集和测试集
x=datas.iloc[:,:-1]#包含9月还款和消费状态
y=datas['Y']
X_train, X_test, y_train, y_test = train_test_split(x, y, random_state=90)random_state是随机数种子,相同的随机数种子可以保证抽取相同的样本,如果不设定种子,下一次跑代码的时候用来训练的样本就会和上一次的不一样。
导入模块和库
#随机森林
#导入所需要的包
from sklearn.metrics import precision_score
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import classification_report#评估报告
from sklearn.model_selection import cross_val_score #交叉验证
from sklearn.model_selection import GridSearchCV #网格搜索
import matplotlib.pyplot as plt#可视化
import seaborn as sns#绘图包
from sklearn.preprocessing import StandardScaler,MinMaxScaler,MaxAbsScaler#归一化,标准化
# 忽略警告
import warnings
warnings.filterwarnings("ignore")默认参数下的随机森林及结果
model=RandomForestClassifier()#建立默认参数的模型
# 训练模型
model.fit(X_train,y_train)
# 预测值
y_pred = model.predict(X_test)
'''
评估指标
'''
# 求出预测和真实一样的数目
true = np.sum(y_pred == y_test )
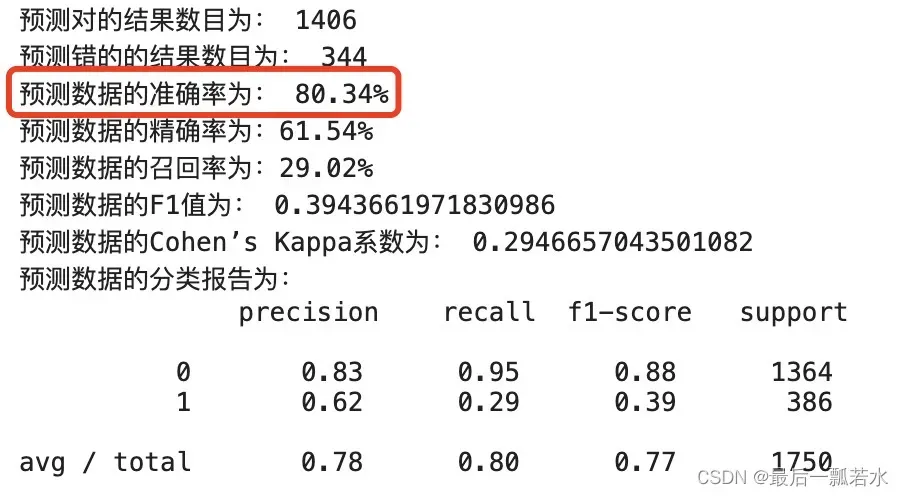
print('预测对的结果数目为:', true)
print('预测错的的结果数目为:', y_test.shape[0]-true)
# 评估指标
from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score,cohen_kappa_score
print('预测数据的准确率为: {:.4}%'.format(accuracy_score(y_test,y_pred)*100))
print('预测数据的精确率为:{:.4}%'.format(precision_score(y_test,y_pred)*100))
print('预测数据的召回率为:{:.4}%'.format(recall_score(y_test,y_pred)*100))
print('预测数据的F1值为:',f1_score(y_test,y_pred))
print('预测数据的Cohen’s Kappa系数为:',cohen_kappa_score(y_test,y_pred))
# 打印分类报告
print('预测数据的分类报告为:','\n',classification_report(y_test,y_pred))默认参数跑出来的准确率达到了80%,说实话也就一般,下面我们进行简单调参,看看能否把准确率往上调一点。
七、调节参数
这里我会用GridSearchCV(网格搜索)对单个参数进行遍历,看看单个最好的参数,组合到一起是否能把准确率往上提一点,当然这样很容易陷入局部最优的陷阱,也可以把最重要的两个参数组合遍历,再对单个参数进行遍历。调参是个很耗时的过程,所以这里以演示帮助理解为主,仅遍历单个参数。
n_estimators ‘种树’(树的数量)
#n_estimators 学习曲线
scorel = []
for i in range(0,200,10):
model = RandomForestClassifier(n_estimators=i+1,
n_jobs=-1,
random_state=90).fit(X_train,y_train)
score = model.score(X_test,y_test)
scorel.append(score)
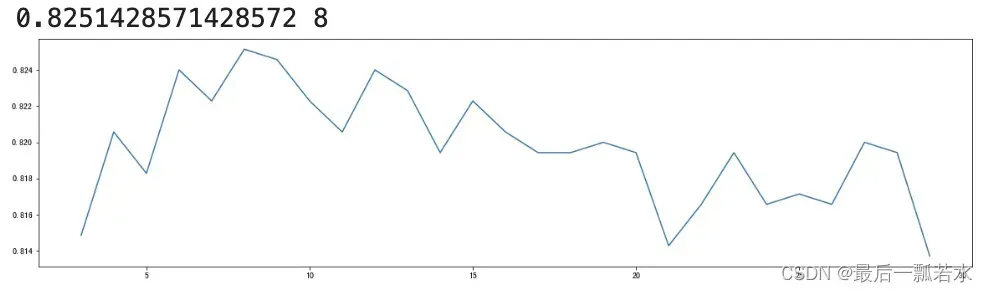
print(max(scorel),(scorel.index(max(scorel))*10)+1) #作图反映出准确度随着估计器数量的变化,71的附近最好
plt.figure(figsize=[20,5])
plt.plot(range(1,201,10),scorel)
plt.show()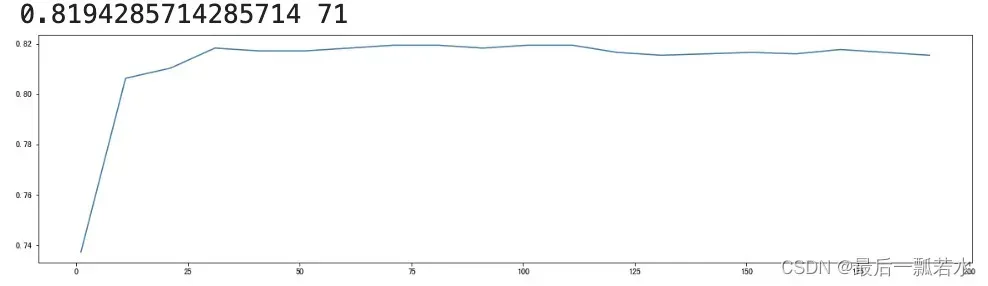
可以看到最优的‘树量’是在71附近,我们在缩小范围看一下。
## 根据上面的显示最优点在71附近,进一步细化学习曲线
scorel = []
for i in range(60,80):
RFC = RandomForestClassifier(n_estimators=i,
n_jobs=-1,
random_state=90).fit(X_train,y_train)
score = RFC.score(X_test,y_test)
scorel.append(score)
print(max(scorel),([*range(60,80)][scorel.index(max(scorel))])) #76是最优的估计器数量
plt.figure(figsize=[20,5])
plt.plot(range(60,80),scorel)
plt.show()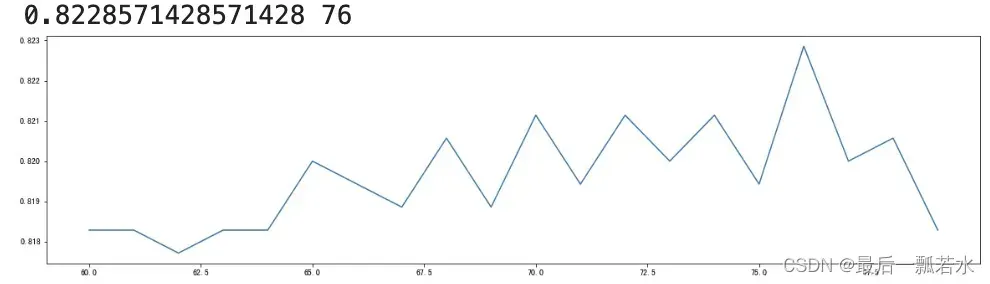
最优的‘树量’是76。
max_depth 优化
scorel = []
for i in range(3,30):
RFC = RandomForestClassifier(max_depth=i,n_estimators=76,
n_jobs=-1,
random_state=90).fit(X_train,y_train)
score = RFC.score(X_test,y_test)
scorel.append(score)
print(max(scorel),([*range(3,30)][scorel.index(max(scorel))]))
plt.figure(figsize=[20,5])
plt.plot(range(3,30),scorel)
plt.show()树的最大深度(max_depth)默认可以不输入,在数据量较大或者特征较多的时候可以限制在10-100之间避免模型太复杂导致过拟合,如果数据量较小或特征不多的情况下是可以不输入的,比如此处数据量也不是很大,可以不用调整。
min_samples_leaf 优化
scorel = []
for i in range(1,20):
RFC = RandomForestClassifier(max_depth=8,n_estimators=76,min_samples_leaf=i,
n_jobs=-1,
random_state=90).fit(X_train,y_train)
score = RFC.score(X_test,y_test)
scorel.append(score)
print(max(scorel),([*range(1,20)][scorel.index(max(scorel))]))
plt.figure(figsize=[20,5])
plt.plot(range(1,20),scorel)
plt.show()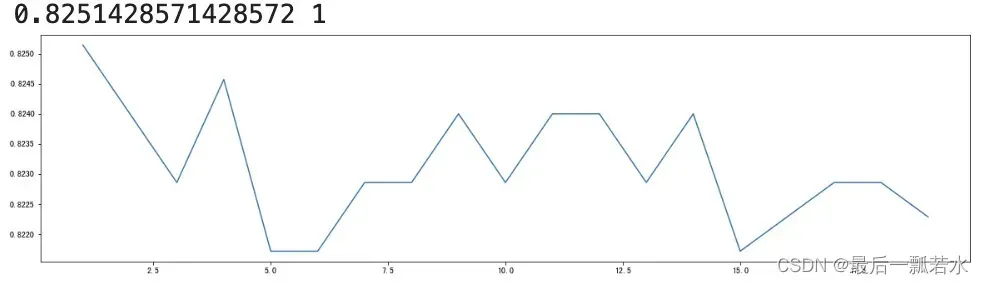
max_features 优化
## 调整max_features
param_grid = {'max_features':['auto', 'sqrt','log2']}
RFC = RandomForestClassifier(max_depth=8,n_estimators=76,min_samples_leaf=1,min_samples_split=7
)
GS = GridSearchCV(RFC,param_grid,cv=10)
GS.fit(X_train,y_train)
print(GS.best_params_ ) #最佳最大特征方法为sqrt
print(GS.best_score_)
criterion 优化
param_grid = {'criterion':['gini', 'entropy']}
RFC = RandomForestClassifier(max_depth=8,n_estimators=76,min_samples_leaf=1,min_samples_split=7,max_features='sqrt')
GS = GridSearchCV(RFC,param_grid,cv=10)
GS.fit(X_train,y_train)
print(GS.best_params_ )
print(GS.best_score_)min_samples_leaf 优化
param_grid = {'min_samples_leaf':np.arange(1, 11, 1)}
RFC = RandomForestClassifier(max_depth=8,n_estimators=76,min_samples_leaf=1,min_samples_split=7,max_features='sqrt',criterion='entropy')
GS = GridSearchCV(RFC,param_grid,cv=10)
GS.fit(X_train,y_train)
print(GS.best_params_ )
print(GS.best_score_) 
可以看到就这样一步一步调也把准确度提高了差不多3%,但是这里调的很简陋,还有很多组合调参的方式值得一一尝试。
随机森林-特征筛选
我们用RandomForestClassifier自带的特征重要性函数,看一下哪些是重要特征,剔除掉非重要特征,看看效果会不会有提升。
feat_labels = datas.columns[:-1]
# n_jobs 整数 可选(默认=1) 适合和预测并行运行的作业数,如果为-1,则将作业数设置为核心数
RFC= RandomForestClassifier(max_depth=8,n_estimators=76,min_samples_leaf=2,min_samples_split=7,max_features='sqrt',criterion='entropy',
random_state=0, n_jobs=-1)
forest.fit(X_train, y_train)
labe_name=[]
imports=[]
# 下面对训练好的随机森林,完成重要性评估
# feature_importances_ 可以调取关于特征重要程度
importances = RFC.feature_importances_
print("重要性:",importances)
x_columns =datas.columns[:-1]
indices = np.argsort(importances)[::-1]
for f in range(X_train.shape[1]):
# 对于最后需要逆序排序,我认为是做了类似决策树回溯的取值,从叶子收敛
# 到根,根部重要程度高于叶子。
print("%2d) %-*s %f" % (f + 1, 30, feat_labels[indices[f]], importances[indices[f]]))
labe_name.append(feat_labels[indices[f]])
imports.append(importances[indices[f]])
# 构造数据
a = pd.DataFrame({"feature": labe_name})
b = pd.DataFrame({"importance": imports})
df = pd.concat([a, b], axis=1)
#作图
sns.barplot(x="importance", y="feature", data=df, order=df["feature"], orient="h")
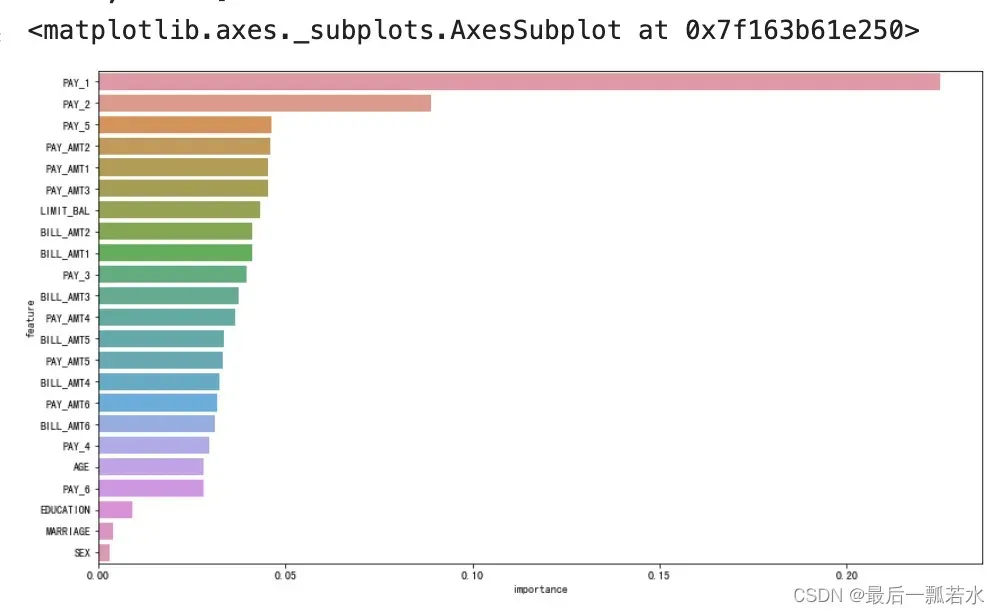
根据排序结果我尝试剔除了SEX、MARRIAGE、EDUCATION三个特征跑了上面训练好的模型,但是效果并没有提升,所以就不展示了,不过随机森林的特征筛选是可以应用到其他模型上的,另外训练随机森林模型时特征输入顺序不一样,得到的结果也会略有差异,但是同为分类模型的Logistic回归模型和Xgboost模型是不用管特征输入顺序的。(这三个是亲测,其他的分类模型以后慢慢试)
八、完整代码自取
#随机森林
#导入所需要的包
from sklearn.metrics import precision_score
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import classification_report#评估报告
from sklearn.model_selection import cross_val_score #交叉验证
from sklearn.model_selection import GridSearchCV #网格搜索
import matplotlib.pyplot as plt#可视化
import seaborn as sns#绘图包
from sklearn.preprocessing import StandardScaler,MinMaxScaler,MaxAbsScaler#归一化,标准化
# 忽略警告
import warnings
warnings.filterwarnings("ignore")
datas=pd.read_csv('data_20221030(1).csv')
datas=datas[datas.columns[2:]]
model=RandomForestClassifier(max_depth=8,n_estimators=76,min_samples_leaf=5,min_samples_split=7,max_features='sqrt',criterion='entropy')
# 训练模型
model.fit(X_train,y_train)
# 预测值
y_pred = model.predict(X_test)
'''
评估指标
'''
# 求出预测和真实一样的数目
true = np.sum(y_pred == y_test )
print('预测对的结果数目为:', true)
print('预测错的的结果数目为:', y_test.shape[0]-true)
# 评估指标
from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score,cohen_kappa_score
print('预测数据的准确率为: {:.4}%'.format(accuracy_score(y_test,y_pred)*100))
print('预测数据的精确率为:{:.4}%'.format(
precision_score(y_test,y_pred)*100))
print('预测数据的召回率为:{:.4}%'.format(
recall_score(y_test,y_pred)*100))
# print("训练数据的F1值为:", f1score_train)
print('预测数据的F1值为:',
f1_score(y_test,y_pred))
print('预测数据的Cohen’s Kappa系数为:',
cohen_kappa_score(y_test,y_pred))
# 打印分类报告
print('预测数据的分类报告为:','\n',
classification_report(y_test,y_pred))文章出处登录后可见!