KMP算法——通俗易懂讲好KMP算法：实例图解分析+详细代码注解 –》你的所有疑惑在本文都能得到解答

1.kmp算法基本介绍

• KMP 是一个解决模式串在文本串是否出现过，如果出现过，最早出现的位置的经典算法。
• Knuth-Morris-Pratt 字符串查找算法，简称为 “KMP 算法”，常用于在一个文本串 S 内查找一个模式串 P 的出现位置，这个算法由Donald Knuth、Vaughan Pratt、James H. Morris 三人于 1977 年联合发表，故取这 3 人的姓氏命名此算法。
• KMP 方法算法就利用之前判断过的信息，通过一个 next 数组，保存模式串中前后最长公共子序列的长度，每次回溯时，通过 next 数组找到，前面匹配过的位置，省去了大量的计算时间。

2.字符串的最长公共前后缀&部分匹配表

2.1 什么是最长公共前后缀

1️⃣ 字符串的前缀是指不包含最后一个字符的所有以第一个字符（索引为0）开头的连续子串

比如字符串 “ABABA” 的前缀有：A，AB，ABA，ABAB

2️⃣ 字符串的后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串

比如字符串 “ABABA” 的后缀有：BABA，ABA，BA，A

3️⃣ 公共前后缀：一个字符串的 所有前缀连续子串 和 所有后缀连续子串 中相等的子串

比如字符串 “ABABA”

• 前缀有：A，AB，ABA，ABAB
• 后缀有：BABA，ABA，BA，A

因此公共前后缀有：A ，ABA

4️⃣ 最长公共前后缀：所有公共前后缀 的 长度最长的 那个子串

比如字符串 “ABABA” ，公共前后缀有：A ，ABA

由于 ABA 是 三个字符长度，A 是一个字符长度，那么最长公共前后缀就是 ABA

📝 再比如说一个字符串 str = “ABCABD”

• 对于str从 索引为0 开始的子串 “A” 而言：

  1. 前缀：不包含最后一个字符A的 所有以第一个字符A开头 的 连续子串 不存在
  2. 后缀：不包含第一个字符A 的 所有以最后一个字符A结尾 的 连续子串 不存在

  因此该子串的最长公共前后缀 为 0

• 对于str从 索引为0 开始的子串 “AB” 而言：

  1. 前缀：不包含 最后一个字符B 的 所有以第一个字符A开头 的 连续子串 有 —— “A”
  2. 后缀：不包含 第一个字符A 的 所有以最后一个字符B结尾 的 连续子串 有 —— “B”

  因此该子串的最长公共前后缀 为 0

• 对于str从 索引为0 开始的子串 “ABC” 而言：

  1. 前缀：不包含 最后一个字符C 的 所有以第一个字符A开头 的 连续子串 有 —— “A”，“AB”
  2. 后缀：不包含 第一个字符A 的 所有以最后一个字符C 结尾 的 连续子串有 —— “BC”，“C”

  前缀与后缀的连续子串不存在相同的，因此该子串的最长公共前后缀 为 0

• 对于str从 索引为0 开始的子串 “ABCA” 而言：

  1. 前缀：不包含 最后一个字符A 的 所有以第一个字符A开头 的 连续子串 有 —— “A”，“AB”，“ABC”
  2. 后缀：不包含 第一个字符A 的 所有以最后一个字符A 结尾 的 连续子串有 —— “BCA”，“CA”，“A”

  前缀与后缀的连续子串中存在相同且最长的子串 A，因此该子串的最长公共前后缀 为 1

• 对于str从 索引为0 开始的子串 “ABCAB” 而言：

  1. 前缀：不包含 最后一个字符B 的 所有以第一个字符A开头 的 连续子串 有 —— “A”，“AB”，“ABC”，“ABCA”
  2. 后缀：不包含 第一个字符A 的 所有以最后一个字符B 结尾 的 连续子串有 —— “BCAB”，“CAB”，“AB”，“B”

  前缀与后缀的连续子串中存在相同且最长的子串 AB，因此该子串的最长公共前后缀 为 2

• 对于str从 索引为0 开始的子串 “ABCABD” 而言：

  1. 前缀：不包含 最后一个字符D 的 所有以第一个字符A开头 的 连续子串 有 —— “A”，“AB”，“ABC”，“ABCA”，“ABCAB”
  2. 后缀：不包含 第一个字符A 的 所有以最后一个字符D 结尾 的 连续子串有 —— “BCABD”，“CABD”，“ABD”，“BD”，“D”

  前缀与后缀的连续子串不存在相同的，因此该子串的最长公共前后缀 为 0

2.2 什么是部分匹配表Next

个人理解：对于字符串str，从 第一个字符开始的每个子串 的 最后一个字符 与 该子串的最长公共前后缀的长度 的对应关系表格。这个表我们以 int[] next 数组方式进行存储。

比如说上面举的例子：

• 子串 “A”：最后一个字符是 A，该子串的最长公共前后缀长度是 0，因此对应关系就是 A – 0
• 子串 “AB”：最后一个字符是 B，该子串的最长公共前后缀长度是 0，因此对应关系就是 B – 0
• 子串 “ABC”：最后一个字符是 C，该子串的最长公共前后缀长度是 0，因此对应关系就是 C – 0
• 子串 “ABCA”：最后一个字符是 A，该子串的最长公共前后缀长度是 1，因此对应关系就是 A – 1
• 子串 “ABCAB”：最后一个字符是 B，该子串的最长公共前后缀长度是 2，因此对应关系就是 B – 2
• 子串 “ABCABD”：最后一个字符是 D，该子串的最长公共前后缀长度是 0，因此对应关系就是 D – 0

因此综上，我们说该字符串 str 的部分匹配表为：

那么对应的next数组就是 int[] next = {0, 0, 0, 1, 2, 0}

2.3 字符串最长公共前后缀&部分匹配表的代码实现

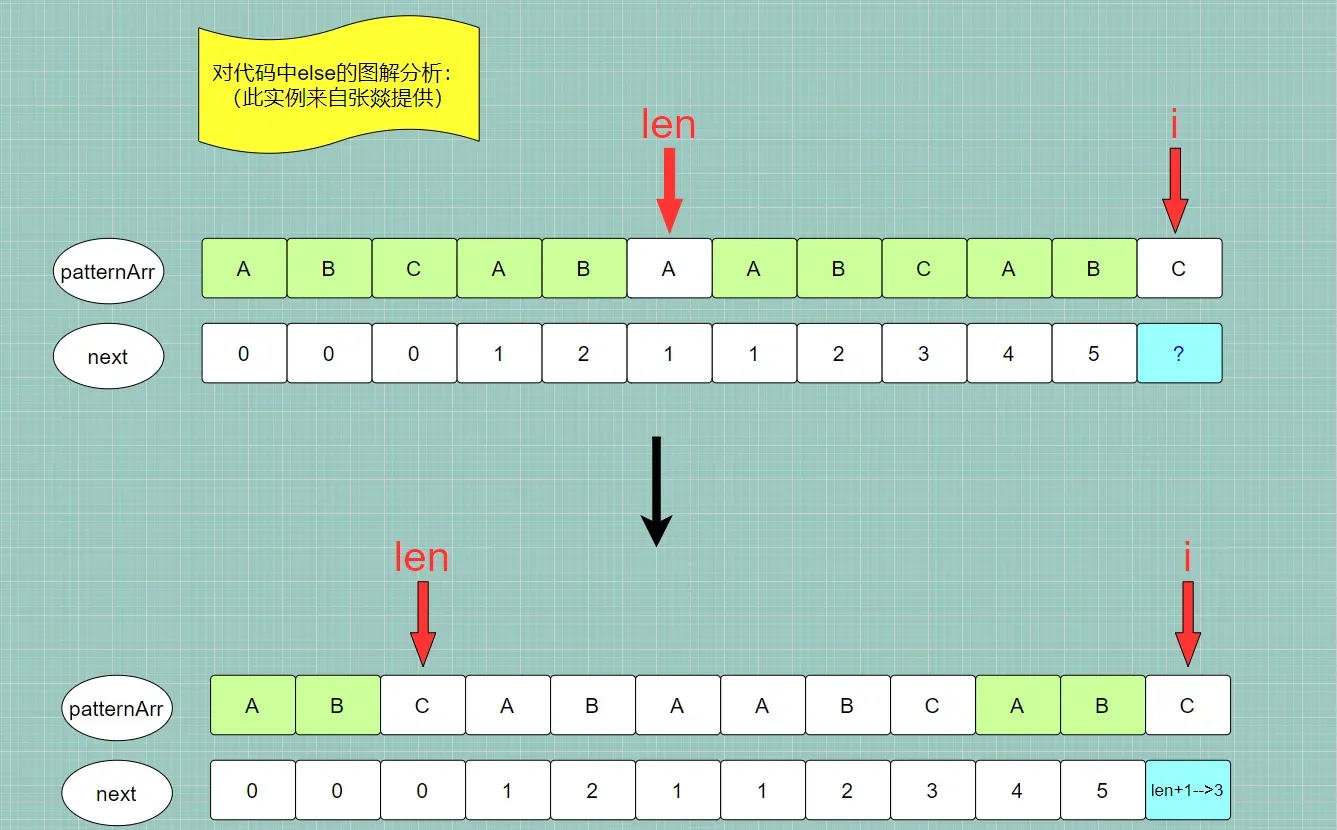
下面的代码可以参考图中实例进行分析：

    /**
     * 获取一个字符串 pattern 的部分匹配表
     *
     * @param patternStr 用于模式匹配字符串
     * @return 存储部分匹配表的每个子串的最长公共前后缀的 next数组
     */
    public static int[] kmpNext(String patternStr) {
        //将 patternStr 转为 字符数组形式
        char[] patternArr = patternStr.toCharArray();

        //预先创建一个next数组，用于存储部分匹配表的每个子串的最长公共前后缀
        int[] next = new int[patternStr.length()];

        /*
            从第一个字符（对应索引为0）开始的子串，如果子串的长度为1，那么肯定最长公共前后缀为0
            因为这唯一的一个字符既是第一个字符，又是最后一个字符，所以前后缀都不存在 -> 最长公共前后缀为0
         */
        next[0] = 0;

        /*
          len有两个作用：
            1. 用于记录当前子串的最长公共前后缀长度
            2. 同时知道当前子串的最长公共前后缀的前缀字符串对应索引 [0,len-1]/当前子串最长公共前缀字符串的下一个字符的索引  <-- 可以拿示例分析一下
         */
        int len = 0;

        //从第二个字符开始遍历，求索引在 [0,i] 的子串的最长公共前后缀长度
        int i = 1;
        while (i < patternArr.length) {
            /*
                1.已经知道了上一个子串 对应索引[0,i-1] 的最长公共前后缀长度为 len
                  的前缀字符串是 索引[0,len-1]，对应相等的后缀字符串是 索引[i-len,i-1]

                2.因此我们可以以 上一个子串的最长公共前后缀字符串 作为拼接参考
                  比较一下 patternArr[len] 与 patternArr[i] 是否相等
             */
            if (patternArr[len] == patternArr[i]) {
                /*
                    1.如果相等即 patternArr[len]==patternArr[i]，
                      那么就可以确定当前子串的最长公共前后缀的
                      前缀字符串是 索引[0,len] ，对应相等的后缀字符串是 索引[i-len,i]

                    2.由于是拼接操作，那么当前子串的最长公共前后缀长度只需要在上一个子串的最长公共前后缀长度的基础上 +1 即可
                      即 next[i] = next[i-1] + 1 ，

                    3.由于 len 是记录的子串的最长公共前后缀长度，对于当前我们所在的代码位置而言
                      len 还是记录的上一个子串的最长公共前后缀长度，因此：
                      next[i] = next[i-1] + 1 等价于 next[i] = ++len
                 */

                // 等价于 next[i] = next[i-1] + 1
                next[i] = ++len;
                //既然找到了索引在[0,i]的子串的最长公共前后缀字符串长度，那就 i+1 去判断以下一个字符结尾的子串的最长公共前后缀长度
                i++;
            }else {
                /*
                    1.如果不相等 patternArr[len]!=patternArr[i]
                      我们想要求当前子串 对应索引[0,i] 的最长公共前后缀长度
                      我们就不能以 上一个子串的最长公共前后缀：前缀字符串pre  后缀字符串post （毫无疑问pre==post） 作为拼接参考

                    2.但可以思考一下：
                      pre的最长公共前缀字符串： 索引 [      0        , next[len-1] )
                      是等于
                      post的最长公共后缀字符串：索引 [ i-next[len-1] ,     i       )

                      则我们 就以 pre的最长公共前缀字符串/post的最长公共后缀字符串 作为拼接参考
                      去判断 pre的最长公共前缀字符串的下一个字符patternArr[next[len-1]] 是否等于 post的最长公共后缀字符串的下一个字符patternArr[i]

                    3.在第 1,2 步分析的基础上
                      我们可以在判断出 patternArr[len]!=patternArr[i] 后，
                      不去执行第二步：patternArr[next[len-1]] 是否等于 patternArr[i]，
                      可以先修改len的值：len = next[len-1]，len就成了 pre的最长公共前缀字符串长度/post的最长公共后缀字符串长度，
                      修改完之后，再去判断下一个字符 是否相等，即 判断 patternArr[len] 是否等于 patternArr[i]
                      仔细观察，这不又是在判断 这个循环中 if-else 语句吗

                    4.关于 len 这个值，在循环开始时我们解释的是：上一个子串的最长公共前后缀字符串的长度
                      但实际上我们在这里改为 len = next[len-1] 表示上一个子串的最长公共前后缀字符串的最长公共前后缀字符串的长度
                      是没有问题的，等价于上一个子串的较小的公共前后缀字符串。
                      既然进入了 else 语句说明字符不相等，就不能以 上一个子串的最长公共前后缀字符串 作为 拼接参考，就应当去缩小参考范围。
                 */
                if(len==0) {

                    /*
                        len为0说明上一个子串已经没有了公共前后缀字符串
                        则我们没有继续寻找的必要 --> 索引在[0, i]的当前子串的最长公共前后缀字符串长度就是0
                     */
                    next[i] = len;

                    //继续寻找下一个字符串的最长公共前后缀字符串长度
                    i++;

                }else{
                    len = next[len - 1];
                }

            }
        }

        return next;
    }

2.4 代码测试

package kmp;

import java.util.Arrays;

/**
 * @author 狐狸半面添
 * @create 2022-11-22 22:43
 */
public class KMPAlgorithm {
    public static void main(String[] args) {
        String patternStr = "ABCDABD";
		//输出结果：[0, 0, 0, 0, 1, 2, 0]
        System.out.println(Arrays.toString(kmpNext(str2)));
    }

    /**
     * 获取一个字符串 pattern 的部分匹配表
     *
     * @param patternStr 用于模式匹配字符串
     * @return 存储部分匹配表的每个子串的最长公共前后缀的 next数组
     */
    public static int[] kmpNext(String patternStr) {
        //将 patternStr 转为 字符数组形式
        char[] patternArr = patternStr.toCharArray();

        //预先创建一个next数组，用于存储部分匹配表的每个子串的最长公共前后缀
        int[] next = new int[patternStr.length()];

        /*
            从第一个字符（对应索引为0）开始的子串，如果子串的长度为1，那么肯定最长公共前后缀为0
            因为这唯一的一个字符既是第一个字符，又是最后一个字符，所以前后缀都不存在 -> 最长公共前后缀为0
         */
        next[0] = 0;

        /*
          len有两个作用：
            1. 用于记录当前子串的最长公共前后缀长度
            2. 同时知道当前子串的最长公共前后缀的前缀字符串对应索引 [0,len-1]/当前子串最长公共前缀字符串的下一个字符的索引  <-- 可以拿示例分析一下
         */
        int len = 0;

        //从第二个字符开始遍历，求索引在 [0,i] 的子串的最长公共前后缀长度
        int i = 1;
        while (i < patternArr.length) {
            /*
                1.已经知道了上一个子串 对应索引[0,i-1] 的最长公共前后缀长度为 len
                  的前缀字符串是 索引[0,len-1]，对应相等的后缀字符串是 索引[i-len,i-1]

                2.因此我们可以以 上一个子串的最长公共前后缀字符串 作为拼接参考
                  比较一下 patternArr[len] 与 patternArr[i] 是否相等
             */
            if (patternArr[len] == patternArr[i]) {
                /*
                    1.如果相等即 patternArr[len]==patternArr[i]，
                      那么就可以确定当前子串的最长公共前后缀的
                      前缀字符串是 索引[0,len] ，对应相等的后缀字符串是 索引[i-len,i]

                    2.由于是拼接操作，那么当前子串的最长公共前后缀长度只需要在上一个子串的最长公共前后缀长度的基础上 +1 即可
                      即 next[i] = next[i-1] + 1 ，

                    3.由于 len 是记录的子串的最长公共前后缀长度，对于当前我们所在的代码位置而言
                      len 还是记录的上一个子串的最长公共前后缀长度，因此：
                      next[i] = next[i-1] + 1 等价于 next[i] = ++len
                 */

                // 等价于 next[i] = next[i-1] + 1
                next[i] = ++len;
                //既然找到了索引在[0,i]的子串的最长公共前后缀字符串长度，那就 i+1 去判断以下一个字符结尾的子串的最长公共前后缀长度
                i++;
            }else {
                /*
                    1.如果不相等 patternArr[len]!=patternArr[i]
                      我们想要求当前子串 对应索引[0,i] 的最长公共前后缀长度
                      我们就不能以 上一个子串的最长公共前后缀：前缀字符串pre  后缀字符串post （毫无疑问pre==post） 作为拼接参考

                    2.但可以思考一下：
                      pre的最长公共前缀字符串： 索引 [      0        , next[len-1] )
                      是等于
                      post的最长公共后缀字符串：索引 [ i-next[len-1] ,     i       )

                      则我们 就以 pre的最长公共前缀字符串/post的最长公共后缀字符串 作为拼接参考
                      去判断 pre的最长公共前缀字符串的下一个字符patternArr[next[len-1]] 是否等于 post的最长公共后缀字符串的下一个字符patternArr[i]

                    3.在第 1,2 步分析的基础上
                      我们可以在判断出 patternArr[len]!=patternArr[i] 后，
                      不去执行第二步：patternArr[next[len-1]] 是否等于 patternArr[i]，
                      可以先修改len的值：len = next[len-1]，len就成了 pre的最长公共前缀字符串长度/post的最长公共后缀字符串长度，
                      修改完之后，再去判断下一个字符 是否相等，即 判断 patternArr[len] 是否等于 patternArr[i]
                      仔细观察，这不又是在判断 这个循环中 if-else 语句吗

                    4.关于 len 这个值，在循环开始时我们解释的是：上一个子串的最长公共前后缀字符串的长度
                      但实际上我们在这里改为 len = next[len-1] 表示上一个子串的最长公共前后缀字符串的最长公共前后缀字符串的长度
                      是没有问题的，等价于上一个子串的较小的公共前后缀字符串。
                      既然进入了 else 语句说明字符不相等，就不能以 上一个子串的最长公共前后缀字符串 作为 拼接参考，就应当去缩小参考范围。
                 */
                if(len==0) {

                    /*
                        len为0说明上一个子串已经没有了公共前后缀字符串
                        则我们没有继续寻找的必要 --> 索引在[0, i]的当前子串的最长公共前后缀字符串长度就是0
                     */
                    next[i] = len;

                    //继续寻找下一个字符串的最长公共前后缀字符串长度
                    i++;

                }else{
                    len = next[len - 1];
                }

            }
        }

        return next;
    }
}

3.根据部分匹配表搜索字符串匹配位置

3.1 匹配成功一个就退出匹配的代码

3.1.1 KMP算法的大致步骤

1. 求出模式字符串patternStr的部分匹配表，已知待匹配的字符串 matchStr

2. 定义两个指针 i 和 j，分别指向 patternStr 和 matchStr ，初始化为0

3. 判断 patternStr[i] 和 matchStr[j] 是否相等

   • 如果相等，则继续向后匹配：i++, j++

   • 如果不相等，则 i 不变，调整 j 为 模式字符串pattern  的 上一个子串（索引 [ 0, j-1 ]）的最长公共前缀字符串的下一个索引位置，该索引位置也是最长公共前缀/后缀字符串的长度：j = next[ j – 1 ]

     解释一下不相等为什么要这样做：

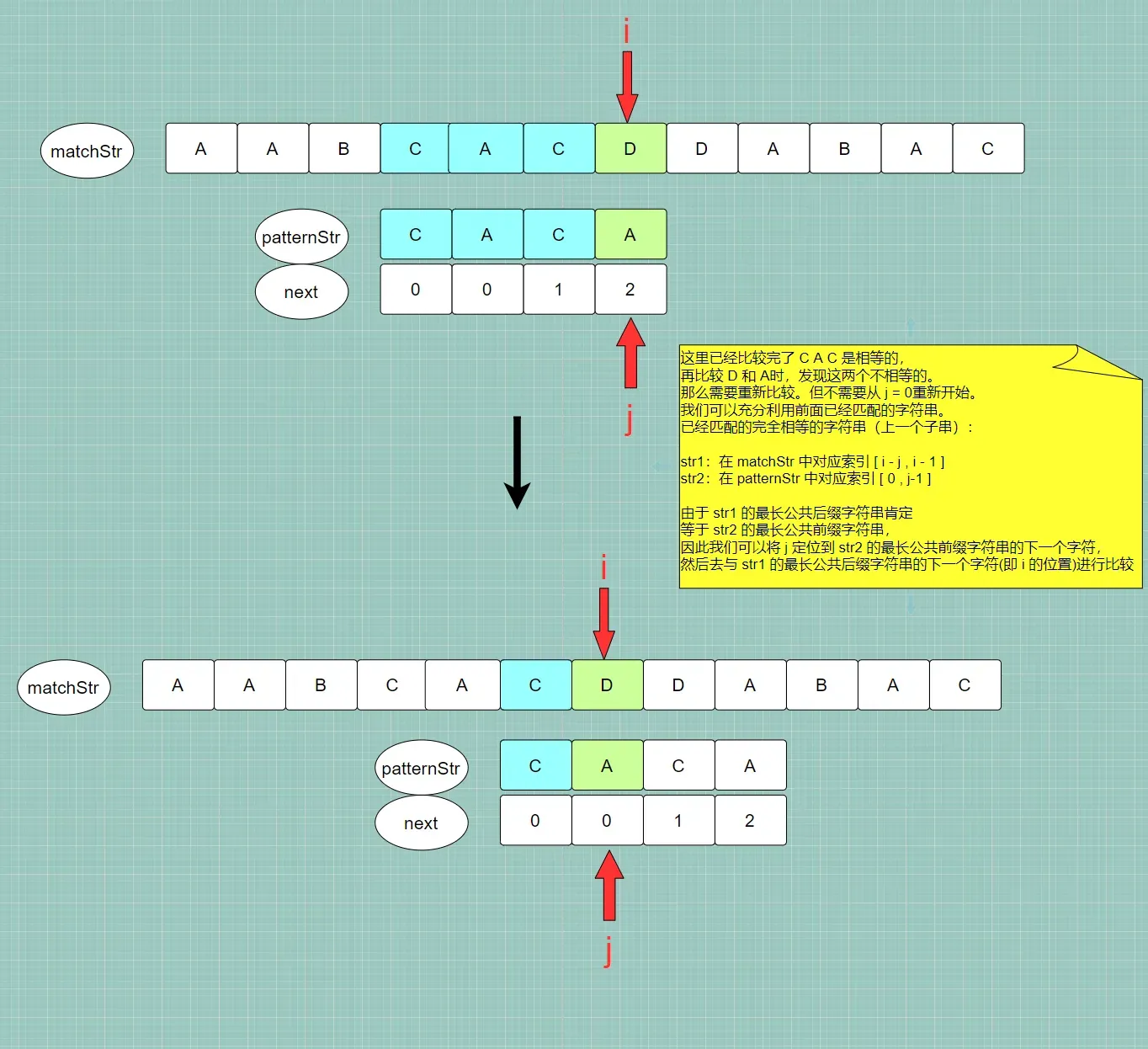
     1️⃣ 在不相等的时候，我们可以知道前面已经匹配的字符串 str1 和 str2 肯定是完全相等的

     • str1：在 matchStr 中对应索引 [ i – j , i – 1 ]
     • str2：在 patternStr 中对应索引 [ 0 , j – 1 ]

     2️⃣ 由于 完全相等，则 str1 的 最长公共后缀字符串 一定等于 str2 的 最长公共前缀字符串，那么：

     • 将 i 定位到 str1 的 最长公共后缀字符串 的 下一个字符位置，但很明显，i 此时的位置肯定已经是在 str1 的最长公共后缀字符串的下一个字符的位置，因此 i 的值不需要做调整
     • 将 j 定位到 str2 的 最长公共前缀字符串 的 下一个字符位置 ，next [ j – 1] 不仅代表 上一个子串str1的最长公共前后缀字符串长度，也是最长公共前缀字符串的下一个字符的索引。因此，我们只需要：j = next[ j – 1 ]

     3️⃣ 修改完毕，我们此时已经匹配的字符串：

     • 在 matchStr 中 对应索引 [ i – j , i – 1 ]
     • 在 patternStr 中 对应索引 [ 0 , j – 1 ]

     4️⃣ 那么我们再继续比较已经匹配的字符串后面的字符就可以了，即 判断 patternStr[i] 和 matchStr[j] 是否相等，这又回到了 步骤三！！！

     

4. 判断 i 和 j 是否超出 各自的最大索引值

   • 如果都没到超出 各自最大索引值，就继续执行第三步进行比较（说明是个循环）
   • 如果至少有一个超出了 各自最大索引值，就退出循环

5. 循环结束后，判断 j 是否超出了 模式字符串的最大索引值

   • 如果超出了，说明匹配成功，返回 patternStr 字符串匹配到的 matchStr 的第一个字符串的起始索引位置：i – j
   • 如果没有超出，说明匹配失败，返回 -1 表示没有匹配到

3.1.2 代码实现+测试

package kmp;

import java.util.Arrays;

/**
 * @author 狐狸半面添
 * @create 2022-11-22 22:43
 */
public class KMPAlgorithm {
    public static void main(String[] args) {
        String matchStr = "AABABADDABAC";
        String patternStr = "ABA";

        // 输出：index = 1
        System.out.println("index = " + kmpSearch(matchStr, patternStr, kmpNext(patternStr)));

    }

    /**
     * kmp搜索算法
     *
     * @param matchStr   原字符串
     * @param patternStr 子串
     * @param next       子串对应的部分匹配表
     * @return 如果是-1，就是没有匹配到，否则就返回第一个匹配的位置
     */
    public static int kmpSearch(String matchStr, String patternStr, int[] next) {

        int i = 0, j = 0;

        while (i < matchStr.length() && j < patternStr.length()) {

            if (matchStr.charAt(i) == patternStr.charAt(j)) {
                //相等就继续进行匹配
                i++;
                j++;

            } else {
                //如果 patternStr[i] 和 matchStr[j] 不相等

                if (j == 0) {
                    /*
                        表示 matchStr 没有匹配到 patternStr的第一个字符
                        那直接将 matchStr 的指针 i 向后移动一位即可
                     */
                    i++;
                } else {
                    j = next[j - 1];
                }
            }

        }
        return j == patternStr.length() ? i - j : -1;
    }

    /**
     * 获取一个字符串 pattern 的部分匹配表
     *
     * @param patternStr 用于模式匹配字符串
     * @return 存储部分匹配表的每个子串的最长公共前后缀的 next数组
     */
    public static int[] kmpNext(String patternStr) {
        //将 patternStr 转为 字符数组形式
        char[] patternArr = patternStr.toCharArray();

        //预先创建一个next数组，用于存储部分匹配表的每个子串的最长公共前后缀
        int[] next = new int[patternStr.length()];

        /*
            从第一个字符（对应索引为0）开始的子串，如果子串的长度为1，那么肯定最长公共前后缀为0
            因为这唯一的一个字符既是第一个字符，又是最后一个字符，所以前后缀都不存在 -> 最长公共前后缀为0
         */
        next[0] = 0;

        /*
          len有两个作用：
            1. 用于记录当前子串的最长公共前后缀长度
            2. 同时知道当前子串的最长公共前后缀的前缀字符串对应索引 [0,len-1]  <-- 可以拿示例分析一下
         */
        int len = 0;

        //从第二个字符开始遍历，求索引在 [0,i] 的子串的最长公共前后缀长度
        int i = 1;
        while (i < patternArr.length) {
            /*
                1.已经知道了上一个子串 对应索引[0,i-1] 的最长公共前后缀长度为 len
                  的前缀字符串是 索引[0,len-1]，对应相等的后缀字符串是 索引[i-len,i-1]

                2.因此我们可以以 上一个子串的最长公共前后缀字符串 作为拼接参考
                  比较一下 patternArr[len] 与 patternArr[i] 是否相等
             */
            if (patternArr[len] == patternArr[i]) {
                /*
                    1.如果相等即 patternArr[len]==patternArr[i]，
                      那么就可以确定当前子串的最长公共前后缀的
                      前缀字符串是 索引[0,len] ，对应相等的后缀字符串是 索引[i-len,i]

                    2.由于是拼接操作，那么当前子串的最长公共前后缀长度只需要在上一个子串的最长公共前后缀长度的基础上 +1 即可
                      即 next[i] = next[i-1] + 1 ，

                    3.由于 len 是记录的子串的最长公共前后缀长度，对于当前我们所在的代码位置而言
                      len 还是记录的上一个子串的最长公共前后缀长度，因此：
                      next[i] = next[i-1] + 1 等价于 next[i] = ++len
                 */

                // 等价于 next[i] = next[i-1] + 1
                next[i] = ++len;
                //既然找到了索引在[0,i]的子串的最长公共前后缀字符串长度，那就 i+1 去判断以下一个字符结尾的子串的最长公共前后缀长度
                i++;
            } else {
                /*
                    1.如果不相等 patternArr[len]!=patternArr[i]
                      我们想要求当前子串 对应索引[0,i] 的最长公共前后缀长度
                      我们就不能以 上一个子串的最长公共前后缀：前缀字符串pre  后缀字符串post （毫无疑问pre==post） 作为拼接参考

                    2.但可以思考一下：
                      pre的最长公共前缀字符串： 索引 [      0        , next[len-1] )
                      是等于
                      post的最长公共后缀字符串：索引 [ i-next[len-1] ,     i       )

                      则我们 就以 pre的最长公共前缀字符串/post的最长公共后缀字符串 作为拼接参考
                      去判断 pre的最长公共前缀字符串的下一个字符patternArr[next[len-1]] 是否等于 post的最长公共后缀字符串的下一个字符patternArr[i]

                    3.在第 1,2 步分析的基础上
                      我们可以在判断出 patternArr[len]!=patternArr[i] 后，
                      不去执行第二步：patternArr[next[len-1]] 是否等于 patternArr[i]，
                      可以先修改len的值：len = next[len-1]，len就成了 pre的最长公共前缀字符串长度/post的最长公共后缀字符串长度，
                      修改完之后，再去判断下一个字符 是否相等，即 判断 patternArr[len] 是否等于 patternArr[i]
                      仔细观察，这不又是在判断 这个循环中 if-else 语句吗

                    4.关于 len 这个值，在循环开始时我们解释的是：上一个子串的最长公共前后缀字符串的长度
                      但实际上我们在这里改为 len = next[len-1] 表示上一个子串的最长公共前后缀字符串的最长公共前后缀字符串的长度
                      是没有问题的，等价于上一个子串的较小的公共前后缀字符串。
                      既然进入了 else 语句说明字符不相等，就不能以 上一个子串的最长公共前后缀字符串 作为 拼接参考，就应当去缩小参考范围。
                 */
                if (len == 0) {

                    /*
                        len为0说明上一个子串已经没有了公共前后缀字符串
                        则我们没有继续寻找的必要 --> 索引在[0, i]的当前子串的最长公共前后缀字符串长度就是0
                     */
                    next[i] = len;

                    //继续寻找下一个字符串的最长公共前后缀字符串长度
                    i++;

                } else {
                    len = next[len - 1];
                }

            }
        }

        return next;
    }
}

3.2 允许匹配多个，可重复索引字符的代码

3.2.1 KMP算法的大致步骤

1. 求出模式字符串patternStr的部分匹配表，已知待匹配的字符串 matchStr
2. 定义两个指针 i 和 j，分别指向 patternStr 和 matchStr ，初始化为0
3. 定义一个 ArrayList 集合 firstIndexList，用于存储每次匹配成功的字符串的开始索引位置
4. 判断 patternStr[i] 和 matchStr[j] 是否相等
   • 如果相等，则继续向后匹配：i++, j++
   • 如果不相等，则 i 不变，调整 j 为 模式字符串pattern  的 上一个子串（索引 [ 0, j-1 ]）的最长公共前缀字符串的下一个索引位置，该索引位置也是最长公共前缀/后缀字符串的长度：j = next[ j – 1 ]
5. 判断 i 是否超出 最大索引值
   • 如果超出了 matchStr 的 最大索引值，就退出循环
6. 判断 j 是否超出了 最大索引值
   • 如果超出了 patternStr 的最大索引值：
     • 将匹配到的字符串的开始索引位置加入到 firstIndexList 集合：firstIndexList.add( i – j )
     • 调整 j 为 模式字符串pattern （索引 [ 0, j-1 ]）的最长公共前缀字符串的下一个索引位置，该索引位置也是最长公共前缀/后缀字符串的长度：j = next[ j – 1 ]。
7. 第五步成立则循环退出，返回 firstIndexList 集合

3.2.2 代码实现+测试

package kmp;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

/**
 * @author 狐狸半面添
 * @create 2022-11-22 22:43
 */
public class KMPAlgorithm {
    public static void main(String[] args) {
        String matchStr = "AABABADDABAC";
        String patternStr = "ABA";

        // 输出：[1, 3, 8]
        System.out.println(kmpSearch(matchStr, patternStr, kmpNext(patternStr)).toString());

    }

    /**
     * kmp搜索算法
     *
     * @param matchStr   原字符串
     * @param patternStr 子串
     * @param next       子串对应的部分匹配表
     * @return 每次匹配成功的字符串的开始索引位置的集合
     */
    public static ArrayList<Integer> kmpSearch(String matchStr, String patternStr, int[] next) {

        int i = 0, j = 0;

        ArrayList<Integer> firstIndexList = new ArrayList<>();

        while (i < matchStr.length()) {

            if (matchStr.charAt(i) == patternStr.charAt(j)) {
                //相等就继续进行匹配
                i++;
                j++;

            } else {
                //如果 patternStr[i] 和 matchStr[j] 不相等

                if (j == 0) {
                    /*
                        表示 matchStr 没有匹配到 patternStr的第一个字符
                        那直接将 matchStr 的指针 i 向后移动一位即可
                     */
                    i++;
                } else {
                    j = next[j - 1];
                }
            }

            if (j == patternStr.length()) {
                //超出了最大索引值
                firstIndexList.add(i - j);
                j = next[j - 1];
            }

        }
        return firstIndexList;
    }

    /**
     * 获取一个字符串 pattern 的部分匹配表
     *
     * @param patternStr 用于模式匹配字符串
     * @return 存储部分匹配表的每个子串的最长公共前后缀的 next数组
     */
    public static int[] kmpNext(String patternStr) {
        //将 patternStr 转为 字符数组形式
        char[] patternArr = patternStr.toCharArray();

        //预先创建一个next数组，用于存储部分匹配表的每个子串的最长公共前后缀
        int[] next = new int[patternStr.length()];

        /*
            从第一个字符（对应索引为0）开始的子串，如果子串的长度为1，那么肯定最长公共前后缀为0
            因为这唯一的一个字符既是第一个字符，又是最后一个字符，所以前后缀都不存在 -> 最长公共前后缀为0
         */
        next[0] = 0;

        /*
          len有两个作用：
            1. 用于记录当前子串的最长公共前后缀长度
            2. 同时知道当前子串的最长公共前后缀的前缀字符串对应索引 [0,len-1]  <-- 可以拿示例分析一下
         */
        int len = 0;

        //从第二个字符开始遍历，求索引在 [0,i] 的子串的最长公共前后缀长度
        int i = 1;
        while (i < patternArr.length) {
            /*
                1.已经知道了上一个子串 对应索引[0,i-1] 的最长公共前后缀长度为 len
                  的前缀字符串是 索引[0,len-1]，对应相等的后缀字符串是 索引[i-len,i-1]

                2.因此我们可以以 上一个子串的最长公共前后缀字符串 作为拼接参考
                  比较一下 patternArr[len] 与 patternArr[i] 是否相等
             */
            if (patternArr[len] == patternArr[i]) {
                /*
                    1.如果相等即 patternArr[len]==patternArr[i]，
                      那么就可以确定当前子串的最长公共前后缀的
                      前缀字符串是 索引[0,len] ，对应相等的后缀字符串是 索引[i-len,i]

                    2.由于是拼接操作，那么当前子串的最长公共前后缀长度只需要在上一个子串的最长公共前后缀长度的基础上 +1 即可
                      即 next[i] = next[i-1] + 1 ，

                    3.由于 len 是记录的子串的最长公共前后缀长度，对于当前我们所在的代码位置而言
                      len 还是记录的上一个子串的最长公共前后缀长度，因此：
                      next[i] = next[i-1] + 1 等价于 next[i] = ++len
                 */

                // 等价于 next[i] = next[i-1] + 1
                next[i] = ++len;
                //既然找到了索引在[0,i]的子串的最长公共前后缀字符串长度，那就 i+1 去判断以下一个字符结尾的子串的最长公共前后缀长度
                i++;
            } else {
                /*
                    1.如果不相等 patternArr[len]!=patternArr[i]
                      我们想要求当前子串 对应索引[0,i] 的最长公共前后缀长度
                      我们就不能以 上一个子串的最长公共前后缀：前缀字符串pre  后缀字符串post （毫无疑问pre==post） 作为拼接参考

                    2.但可以思考一下：
                      pre的最长公共前缀字符串： 索引 [      0        , next[len-1] )
                      是等于
                      post的最长公共后缀字符串：索引 [ i-next[len-1] ,     i       )

                      则我们 就以 pre的最长公共前缀字符串/post的最长公共后缀字符串 作为拼接参考
                      去判断 pre的最长公共前缀字符串的下一个字符patternArr[next[len-1]] 是否等于 post的最长公共后缀字符串的下一个字符patternArr[i]

                    3.在第 1,2 步分析的基础上
                      我们可以在判断出 patternArr[len]!=patternArr[i] 后，
                      不去执行第二步：patternArr[next[len-1]] 是否等于 patternArr[i]，
                      可以先修改len的值：len = next[len-1]，len就成了 pre的最长公共前缀字符串长度/post的最长公共后缀字符串长度，
                      修改完之后，再去判断下一个字符 是否相等，即 判断 patternArr[len] 是否等于 patternArr[i]
                      仔细观察，这不又是在判断 这个循环中 if-else 语句吗

                    4.关于 len 这个值，在循环开始时我们解释的是：上一个子串的最长公共前后缀字符串的长度
                      但实际上我们在这里改为 len = next[len-1] 表示上一个子串的最长公共前后缀字符串的最长公共前后缀字符串的长度
                      是没有问题的，等价于上一个子串的较小的公共前后缀字符串。
                      既然进入了 else 语句说明字符不相等，就不能以 上一个子串的最长公共前后缀字符串 作为 拼接参考，就应当去缩小参考范围。
                 */
                if (len == 0) {

                    /*
                        len为0说明上一个子串已经没有了公共前后缀字符串
                        则我们没有继续寻找的必要 --> 索引在[0, i]的当前子串的最长公共前后缀字符串长度就是0
                     */
                    next[i] = len;

                    //继续寻找下一个字符串的最长公共前后缀字符串长度
                    i++;

                } else {
                    len = next[len - 1];
                }

            }
        }

        return next;
    }
}

3.3 允许匹配多个，不可重复索引字符的代码

3.3.1 KMP算法的大致步骤

1. 求出模式字符串patternStr的部分匹配表，已知待匹配的字符串 matchStr
2. 定义两个指针 i 和 j，分别指向 patternStr 和 matchStr ，初始化为0
3. 定义一个 ArrayList 集合 firstIndexList，用于存储每次匹配成功的字符串的开始索引位置
4. 判断 patternStr[i] 和 matchStr[j] 是否相等
   • 如果相等，则继续向后匹配：i++, j++
   • 如果不相等，则 i 不变，调整 j 为 模式字符串pattern  的 上一个子串（索引 [ 0, j-1 ]）的最长公共前缀字符串的下一个索引位置，该索引位置也是最长公共前缀/后缀字符串的长度：j = next[ j – 1 ]
5. 判断 i 是否超出 最大索引值
   • 如果超出了 matchStr 的 最大索引值，就退出循环
6. 判断 j 是否超出了 最大索引值
   • 如果超出了 patternStr 的最大索引值：
     • 将匹配到的字符串的开始索引位置加入到 firstIndexList 集合：firstIndexList.add( i – j )
     • 设置 j = 0 开始重新匹配
7. 第五步成立则循环退出，返回 firstIndexList 集合

3.3.2 代码实现+测试

package kmp;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

/**
 * @author 狐狸半面添
 * @create 2022-11-22 22:43
 */
public class KMPAlgorithm {
    public static void main(String[] args) {
        String matchStr = "AABABADDABAC";
        String patternStr = "ABA";

        // 输出：[1, 8]
        System.out.println(kmpSearch(matchStr, patternStr, kmpNext(patternStr)).toString());

    }

    /**
     * kmp搜索算法
     *
     * @param matchStr   原字符串
     * @param patternStr 子串
     * @param next       子串对应的部分匹配表
     * @return 每次匹配成功的字符串的开始索引位置的集合
     */
    public static ArrayList<Integer> kmpSearch(String matchStr, String patternStr, int[] next) {

        int i = 0, j = 0;

        ArrayList<Integer> firstIndexList = new ArrayList<>();

        while (i < matchStr.length()) {

            if (matchStr.charAt(i) == patternStr.charAt(j)) {
                //相等就继续进行匹配
                i++;
                j++;

            } else {
                //如果 patternStr[i] 和 matchStr[j] 不相等

                if (j == 0) {
                    /*
                        表示 matchStr 没有匹配到 patternStr的第一个字符
                        那直接将 matchStr 的指针 i 向后移动一位即可
                     */
                    i++;
                } else {
                    j = next[j - 1];
                }
            }

            if (j == patternStr.length()) {
                //超出了最大索引值
                firstIndexList.add(i - j);
                j = 0;
            }

        }
        return firstIndexList;
    }

    /**
     * 获取一个字符串 pattern 的部分匹配表
     *
     * @param patternStr 用于模式匹配字符串
     * @return 存储部分匹配表的每个子串的最长公共前后缀的 next数组
     */
    public static int[] kmpNext(String patternStr) {
        //将 patternStr 转为 字符数组形式
        char[] patternArr = patternStr.toCharArray();

        //预先创建一个next数组，用于存储部分匹配表的每个子串的最长公共前后缀
        int[] next = new int[patternStr.length()];

        /*
            从第一个字符（对应索引为0）开始的子串，如果子串的长度为1，那么肯定最长公共前后缀为0
            因为这唯一的一个字符既是第一个字符，又是最后一个字符，所以前后缀都不存在 -> 最长公共前后缀为0
         */
        next[0] = 0;

        /*
          len有两个作用：
            1. 用于记录当前子串的最长公共前后缀长度
            2. 同时知道当前子串的最长公共前后缀的前缀字符串对应索引 [0,len-1]  <-- 可以拿示例分析一下
         */
        int len = 0;

        //从第二个字符开始遍历，求索引在 [0,i] 的子串的最长公共前后缀长度
        int i = 1;
        while (i < patternArr.length) {
            /*
                1.已经知道了上一个子串 对应索引[0,i-1] 的最长公共前后缀长度为 len
                  的前缀字符串是 索引[0,len-1]，对应相等的后缀字符串是 索引[i-len,i-1]

                2.因此我们可以以 上一个子串的最长公共前后缀字符串 作为拼接参考
                  比较一下 patternArr[len] 与 patternArr[i] 是否相等
             */
            if (patternArr[len] == patternArr[i]) {
                /*
                    1.如果相等即 patternArr[len]==patternArr[i]，
                      那么就可以确定当前子串的最长公共前后缀的
                      前缀字符串是 索引[0,len] ，对应相等的后缀字符串是 索引[i-len,i]

                    2.由于是拼接操作，那么当前子串的最长公共前后缀长度只需要在上一个子串的最长公共前后缀长度的基础上 +1 即可
                      即 next[i] = next[i-1] + 1 ，

                    3.由于 len 是记录的子串的最长公共前后缀长度，对于当前我们所在的代码位置而言
                      len 还是记录的上一个子串的最长公共前后缀长度，因此：
                      next[i] = next[i-1] + 1 等价于 next[i] = ++len
                 */

                // 等价于 next[i] = next[i-1] + 1
                next[i] = ++len;
                //既然找到了索引在[0,i]的子串的最长公共前后缀字符串长度，那就 i+1 去判断以下一个字符结尾的子串的最长公共前后缀长度
                i++;
            } else {
                /*
                    1.如果不相等 patternArr[len]!=patternArr[i]
                      我们想要求当前子串 对应索引[0,i] 的最长公共前后缀长度
                      我们就不能以 上一个子串的最长公共前后缀：前缀字符串pre  后缀字符串post （毫无疑问pre==post） 作为拼接参考

                    2.但可以思考一下：
                      pre的最长公共前缀字符串： 索引 [      0        , next[len-1] )
                      是等于
                      post的最长公共后缀字符串：索引 [ i-next[len-1] ,     i       )

                      则我们 就以 pre的最长公共前缀字符串/post的最长公共后缀字符串 作为拼接参考
                      去判断 pre的最长公共前缀字符串的下一个字符patternArr[next[len-1]] 是否等于 post的最长公共后缀字符串的下一个字符patternArr[i]

                    3.在第 1,2 步分析的基础上
                      我们可以在判断出 patternArr[len]!=patternArr[i] 后，
                      不去执行第二步：patternArr[next[len-1]] 是否等于 patternArr[i]，
                      可以先修改len的值：len = next[len-1]，len就成了 pre的最长公共前缀字符串长度/post的最长公共后缀字符串长度，
                      修改完之后，再去判断下一个字符 是否相等，即 判断 patternArr[len] 是否等于 patternArr[i]
                      仔细观察，这不又是在判断 这个循环中 if-else 语句吗

                    4.关于 len 这个值，在循环开始时我们解释的是：上一个子串的最长公共前后缀字符串的长度
                      但实际上我们在这里改为 len = next[len-1] 表示上一个子串的最长公共前后缀字符串的最长公共前后缀字符串的长度
                      是没有问题的，等价于上一个子串的较小的公共前后缀字符串。
                      既然进入了 else 语句说明字符不相等，就不能以 上一个子串的最长公共前后缀字符串 作为 拼接参考，就应当去缩小参考范围。
                 */
                if (len == 0) {

                    /*
                        len为0说明上一个子串已经没有了公共前后缀字符串
                        则我们没有继续寻找的必要 --> 索引在[0, i]的当前子串的最长公共前后缀字符串长度就是0
                     */
                    next[i] = len;

                    //继续寻找下一个字符串的最长公共前后缀字符串长度
                    i++;

                } else {
                    len = next[len - 1];
                }

            }
        }

        return next;
    }
}