三种坐标系学习

坐标系学习

三种坐标系介绍

1.地心地固坐标系（ECEF）

地心地固坐标系，也叫ECEF坐标系。其原点为地球的质心。

x轴延伸通过本初子午线（0度经度）和赤道（0度纬度）的交点。

Z轴延伸通过北极（即与地球旋转轴重合）。

y轴完成右手坐标系，穿过赤道和90度经度。

如下图所示

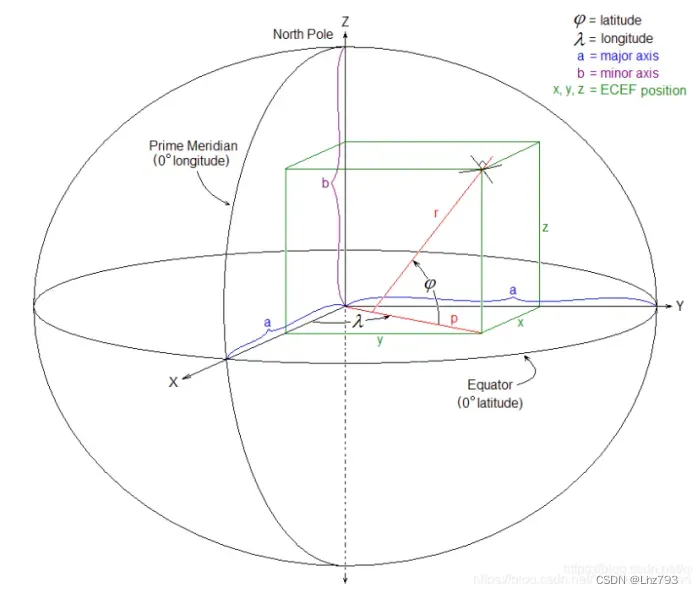
所用的坐标系是右手坐标系（右手定则），将手掌伸直，掌面朝向自己，将中指垂直于掌面，然后将大拇指垂直于中指和食指构成的平面，就构成右手坐标系，此时大拇指，食指，中指分别代表了y轴，z轴，x轴。

2.经纬高坐标系（84坐标系）

经纬高坐标系（84坐标系）是由经度(longitude)，纬度(latitude)，高度(altitude)组成的坐标系，也叫LLA坐标系。可以说是最为广泛的一个坐标系，他给出一点的大地纬度，大地经度和大地高度就可以知道这个点在地球上的位置，所以叫做经纬高坐标系。

84坐标系和上面的ECEF坐标系一样，把ECEF放到GPS中就是84坐标系

1. 大地纬度是过用户点P的基准椭球面法线与赤道面的夹角。纬度在-90度到90度之间，北半球为正，南半球为负
2. 大地经度是过用户点P的子午面与本初子午线之间的夹角。经度值在-180度到180之间
3. 大地高度h是过用户点P到基准椭球面的法线距离，基准椭球面里面为负，外面为正

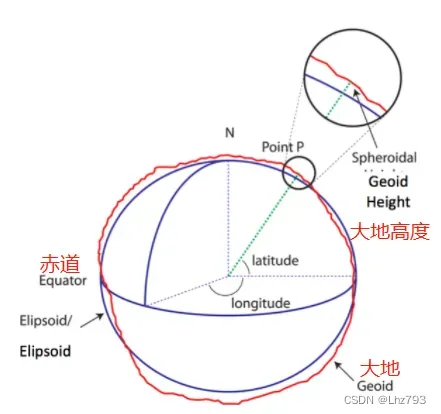
3.东北天坐标系（ENU）

东北天坐标系也叫站心坐标系，以用户所在位置P为坐标原点

坐标轴定义：x轴指向东边，y轴指向北边，z轴指向天顶

简介：ENU局部坐标系采用三维直角坐标系来描述地球表面，实际应用比较困难，因此一般使用简化后的二维投影坐标系来描述，在众多二维投影坐标系中，统一横轴墨卡托（UTM）坐标系是一种应用较为广泛的一种。UTM坐标系统使用基于网格的方法表示坐标，他将地球分为60个经度区，每个区包含6度的精度范围，每个区内的坐标均基于横轴墨卡托投影，如下图所示：

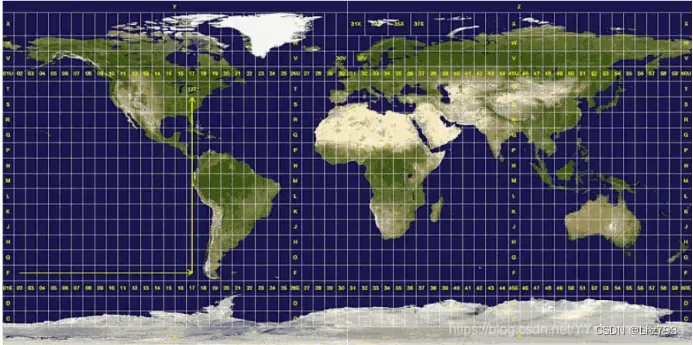
坐标系之间的转换

1.WGS84–ECEF

需要用到的参数：

地球长半轴半径：a

地球短半轴半径：b

椭球的第一偏心率：e

卯酉圈半径：N

输入：

经度（Lon），纬度（Lat），高度（Ait）

计算：

偏心率：e = sqart(a*a – b*b) / a;

卯酉圈半径：N = a/sqart(1-e*e*sin(Lat)*sin(Lat));

输出X,Y,Z

X = (N+Ait)*cos(Lat)*cos(Lon);

Y = (N+Ait)*cos(Lat)*sin(Lon);

Z =(N*(1-e*e)+Ait)*sin(Lat);

1. ECEF–ENU

坐标原点P0（x0, y0, z0），计算点P（x, y, z）以P0为坐标原点的ENU坐标系位置，这里用到的P0的经纬度LLA（lon0, lat0, alt0）。

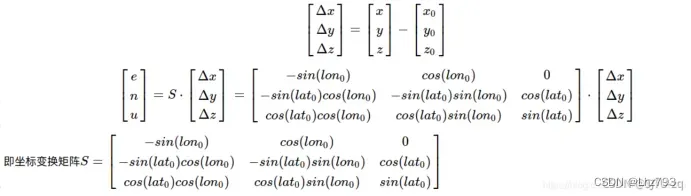
代码：

1. // ECEF->ENU
2.   Re = R0 / sqrt(1 – e * e * sin(p.latitude * torad) * sin(p.latitude * torad));
3.     double dx_ECEF = (Re + p.height) * cos(p.latitude * torad) * cos(p.longitude * torad) – x0_ECEF;
4.     double dy_ECEF = (Re + p.height) * cos(p.latitude * torad) * sin(p.longitude * torad) – y0_ECEF;
5.     double dz_ECEF = (Re * (1 – e * e) + p.height) * sin(p.latitude * torad) – z0_ECEF;
7.     double x = –sin(p.longitude * torad) * dx_ECEF + cos(p.longitude * torad) * dy_ECEF;
8.     double y = –sin(p.latitude * torad) * cos(p.longitude * torad) * dx_ECEF – sin(p.latitude * torad) * sin(p.longitude * torad) * dy_ECEF + cos(p.latitude * torad) * dz_ECEF;
9.     double z = cos(p.latitude * torad) * cos(p.longitude * torad) * dx_ECEF + cos(p.latitude * torad) * sin(p.longitude * torad) * dy_ECEF + sin(p.latitude * torad) * dz_ECEF;

1. ENU-ECEF

公式转化

1. ECEF-WGS84

ECEF坐标系下点(X,Y,Z)转换为LLA坐标系下的(lon,lat,alt)

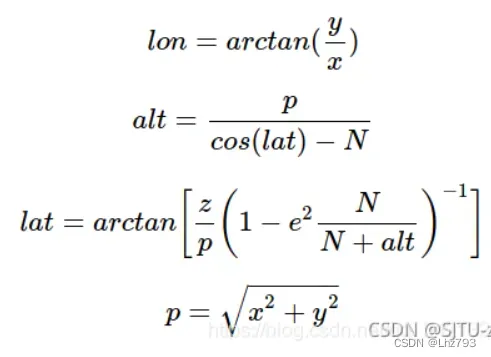
1. WGS84-ENU

公式转化

上述可以看到，从LLA坐标系转换到enu坐标系有较多计算量，在考虑地球偏心率e ee很小的前提下，可以做一定的近似公式计算

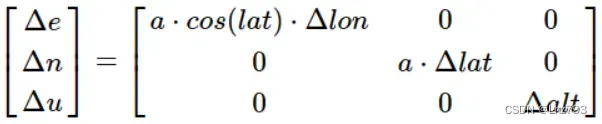
代码：

1. //LLA->ENU
2. void gps2xy(const &p, const double &ori_longitude, const double &ori_latitude, const double &ori_height)
3. {
4.     double R0 = 6378137.0;
5.     const double e = 0.0818191908425;
6.     const double torad = M_PI / 180;
8.     double Re = R0 / sqrt(1 – e * e * sin(ori_latitude * torad) * sin(ori_latitude * torad));
9.     double x0_ECEF = (Re + ori_height) * cos(ori_latitude * torad) * cos(ori_longitude * torad);
10.     double y0_ECEF = (Re + ori_height) * cos(ori_latitude * torad) * sin(ori_longitude * torad);
11.     double z0_ECEF = (Re * (1 – e * e) + ori_height) * sin(ori_latitude * torad);
12.     Re = R0 / sqrt(1 – e * e * sin(p.latitude * torad) * sin(p.latitude * torad));
13.     double dx_ECEF = (Re + p.height) * cos(p.latitude * torad) * cos(p.longitude * torad) – x0_ECEF;
14.     double dy_ECEF = (Re + p.height) * cos(p.latitude * torad) * sin(p.longitude * torad) – y0_ECEF;
15.     double dz_ECEF = (Re * (1 – e * e) + p.height) * sin(p.latitude * torad) – z0_ECEF;
17.     // ECEF to ENU
18.     double x = –sin(p.longitude * torad) * dx_ECEF + cos(p.longitude * torad) * dy_ECEF;
19.     double y = –sin(p.latitude * torad) * cos(p.longitude * torad) * dx_ECEF – sin(p.latitude * torad) * sin(p.longitude * torad) * dy_ECEF + cos(p.latitude * torad) * dz_ECEF;
20.     double z = cos(p.latitude * torad) * cos(p.longitude * torad) * dx_ECEF + cos(p.latitude * torad) * sin(p.longitude * torad) * dy_ECEF + sin(p.latitude * torad) * dz_ECEF;
21. }