线性代数知识点整理

目录

前言

        为了更好的学习深度学习的相关内容，笔者重新整理了线性代数的主要内容，并以知识点摘要的形式对各部分进行了总结，留待之后进行相关概念的快速复习。

一.行列式

1.行列式求值

参考行列式求值

2.七大性质

3.特殊行列式的值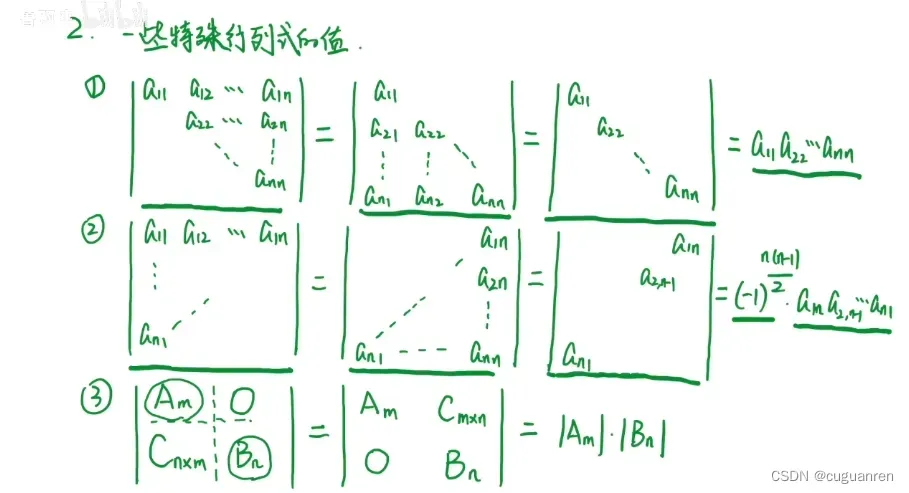

二.矩阵及其运算

  1.行列向量：

在线性代数中，列向量是一个 n×1 的矩阵，即矩阵由一个含有n个元素的列所组成：列向量的转置是一个行向量，反之亦然。

  2.可逆矩阵：

矩阵A为n阶方阵，若存在n阶矩阵B，使得矩阵A、B的乘积为单位阵，则称A为可逆阵，B为A的逆矩阵。 若方阵的逆阵存在，则称为可逆矩阵或非奇异矩阵，且其逆矩阵唯一。 A是可逆矩阵的充分必要条件是︱A︱≠0（方阵A的行列式不等于0）。A 的秩等于n（A 满秩）。

  3.常用性质：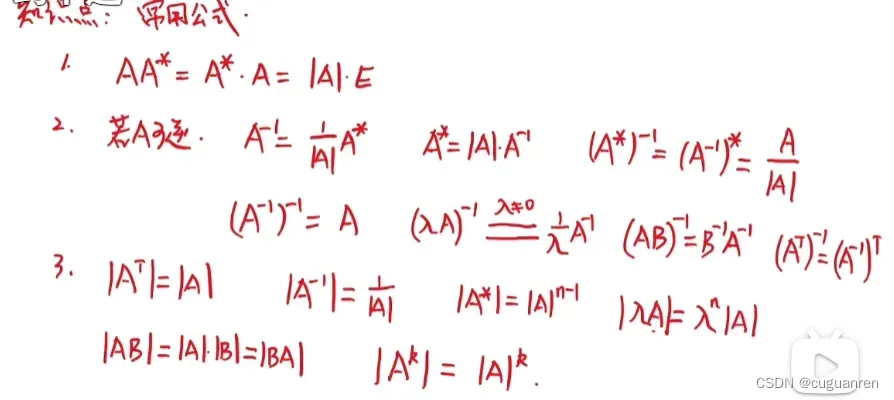

4.伴随矩阵：

三.矩阵的初等变换和线性方程组

1.初等变换：

单位矩阵通过三种变换形式得到的矩阵叫做初等矩阵

①行间或列间互换②行或列乘k倍③某行加上另一行的k倍（列也如此）

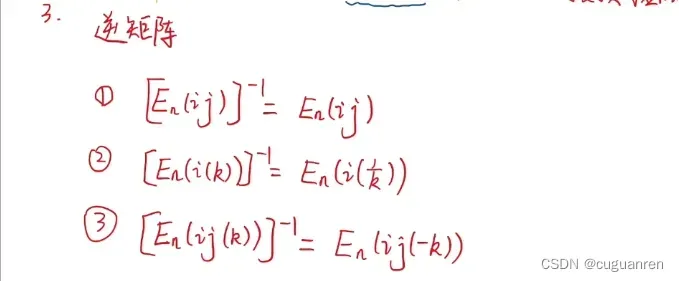
2.矩阵的秩：定义，特性，求秩

细致内容参考矩阵的秩，重点强调：可逆矩阵是满秩矩阵

3.齐次与非齐次线性方程组

①两者区别

齐次线性方程组的常数项全部为零，非齐次方程组的常数项不全为零。

②表达式不同：

齐次线性方程组表达式 ：Ax=0；非齐次方程组程度常数项不全为零： Ax=b。A称为系数矩阵，等号右边是常数项。

③增广矩阵

又称 广置矩阵 ，是在 线性代数中系数矩阵A的右边添上线性方程组等号右边的常数列得到的矩阵，用矩阵（A|B）表示

④两种方程组的解

⑤最简行/列阶梯矩阵：

1.只能行变换 2.化简时，从左上角第一个非零元素开始，其下元素需全部化为零，再找阶梯下一个元素，其下元素化为零 3.行阶梯接着可化为行最简，阶梯每行左起第一个元素为1 4.行变换只能化为行最简，列一样

因此，不能交叉使用两种变换得到一种最简矩阵

4.等价矩阵：

在线性代数和矩阵论中，有两个m×n阶矩阵A和B，如果这两个矩阵满足B=QAP（P是n×n阶可逆矩阵，Q是m×m阶可逆矩阵），那么这两个矩阵之间是等价关系。 也就是说，存在可逆矩阵（P、Q)，使得A经过有限次的初等变换得到B。

四.向量组的线性相关性

1.线性表示：

对于两个向量组：两个向量组A、B，若A组中每一个向量都可以由向量组B线性表示，则称向量组A可由向量组B线性表示。（向量b能由向量组X线性表示的充要条件是：R(A)=R(A,B)）

系数矩阵在左边时可以认为是对行进行线性变换，在右边时可以认为对列进行线性变换

2.线性相关性判断：

定义由第一种方法给出，A向量组的构成元素ai都是向量

初等行变换不改变列向量的线性相关性，也不改变行向量的线性相关性。

3.解的情况

五.相似矩阵以及二次型

只有方阵具有特征值与特征向量，不同特征值所对应的特征向量之间线性无关

形象的例子：如果把矩阵看作运动的话，那么

• 特征值就是运动的速度

• 特征向量是运动的方向

1.特征值和特征向量的定义

实数λ为特征值，向量p为特征向量

2.特征值和特征向量的求解

3.特征值和特征向量的性质

4.矩阵的相似对角化

存在可逆矩阵P使得矩阵A满足P-1 A P =A的对角矩阵（尖符号），则A称为可以相似对角化

5.特征分解和对角矩阵

6.二次化标准型

考虑到对于深度学习来说，此部分不太重要，暂时进行了略过，留待后日补充。