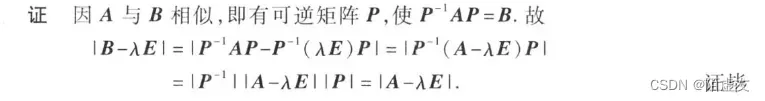目录
一、行列式
1.1 概念

二阶行列式
数(i=1,2;j=1,2)称为二行列式的元素或元
元素的第一个下标 i 称为行标,表明该元素位于第i行;
第二个下标 j 称为列标表明该元素位于第j列.位于第i行第j列的元素称为行列式的(i,j)元.
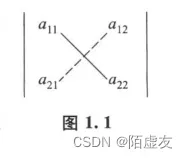
参看图1.1,把a11到a22的实连线称为主对角线,a12到a21的虚连线称为副对角线,于是二阶行列式的值便是主对角线上的两元素之积减去副对角线上两元素之积所得的差.
所以我们要知道的是:行列式最终代表的是一个数值,是一个数
1.2 逆序数
全排列:把n个不同的元素排成一列,叫做这n个元素的全排列(也简称排列).
如 12345678
逆序数:对于n个不同的元素,先规定各元素之间有一个标准次序(例如n个不同的自然数,可规定由小到大为标准次序),于是在这n个元素的任一排列中,当某一对元素的先后次序与标准次序不同时,就说它构成1个逆序.一个排列中所有逆序的总数叫做这个排列的逆序数.
逆序数为奇数的排列叫做奇排列,逆序数为偶数的排列叫做偶排列.
如 24513,它的逆序数为5,则它是奇排列
对换:在排列中,将任意两个元素对调,其余的元素不动,这种作出新排列的手续叫做对换.将相邻两个元素对换,叫做相邻对换.
由对换我们可以引入逆序数的定理及推论:
- 定理1 一个排列中的任意两个元素对换,排列改变奇偶性.
- 推论 奇排列对换成标准排列的对换次数为奇数,偶排列对换成标准排列的对换次数为偶数.
1.3 行列式的计算
二阶行列式的计算及是主对角线上的两元素之积减去副对角线上两元素之积所得的差.我们主要讨论高阶行列式的计算
1.3.1 公式法
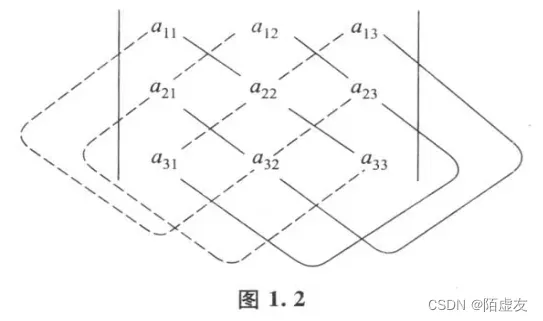
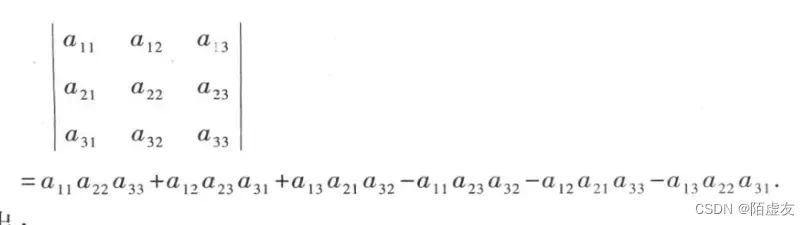
我们可以用以下公式直接计算三阶及n阶行列式的值
t为p1p2…pn的逆序数
1.3.2 三角形法
三角形行列式: 主对角线以下(上)的元素都为0的行列式叫做上(下)三角形行列式;特别,主对角线以下和以上的元素都为0的行列式叫做对角行列式.
计算方法我们直接上例题


1.3.3 按行按列展开(做题推荐首要考虑此方法)
余子式:在n阶行列式中,把(i,j)元所在的第i行和第j列划去后,留下来的n-1阶行列式叫做(i,j)元
的余子式,记作Mij;记

- 定理2 行列式等于它的任一行(列)的各元素与其对应的代数余子式乘积之和,即
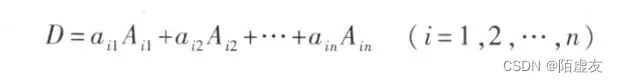
- 引理 一个n阶行列式,如果其中第i行所有元素除(i,j)元
外都为零,那么这行列式等于
与它的代数余子式的乘积,即D=
- 推论 行列式某一行(列)的元素与另一行(列)的对应元素的代数余子式乘积之和等于零.
例题

1.4 行列式的性质
记行列式DT称为行列式D的转置行列式.
- 性质1 行列式与它的转置行列式相等.
性质1证明:
由此性质可知,行列式中的行与列具有同等的地位,行列式的性质凡是对行成立的对列也同样成立,反之亦然.
- 性质2 对换行列式的两行(列),行列式变号.
性质2 证明:
- 推论 如果行列式有两行(列)完全相同,则此行列式等于零.
证 把这两行对换,有D=-D,故D=0.证毕
- 性质3 行列式的某一行(列)中所有的元素都乘同一数k,等于用数k乘此行列式
- 推论 行列式中某一行(列)的所有元素的公因子可以提到行列式记号的外面.

- 性质4 行列式中如果有两行(列)元素成比例,则此行列式等于零.
- 性质5 若行列式的某一行(列)的元素都是两数之和,例如第i行的元素都是两数之和,则D等于下列两个行列式之和:

- 性质6 把行列式的某一行(列)的各元素乘同一数然后加到另一行(列)对应的元素上去,行列式不变.
例题(范德蒙行列式)
证明:
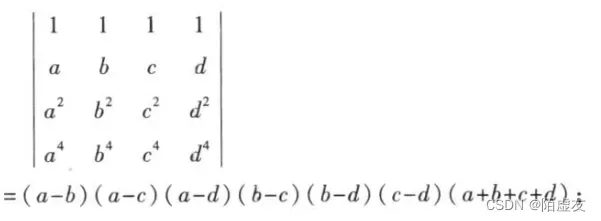

二、矩阵
2.1 矩阵的定义
由mn个数
(i=1,2,…,m; j=1,2,…,n)排成的m行n列的数表称为m行n列矩阵,简称m
n矩阵,为表示它是一个整体,总是加一个括弧,并用大写黑体字母表示它,记作:
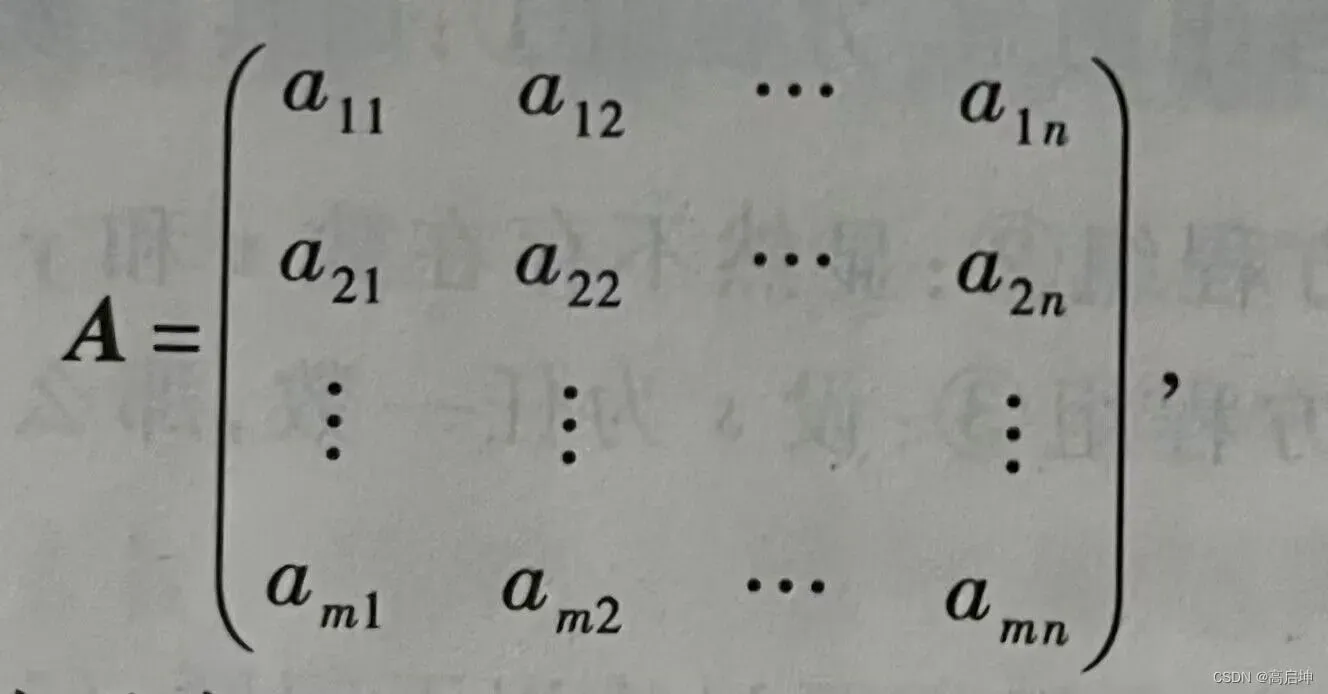
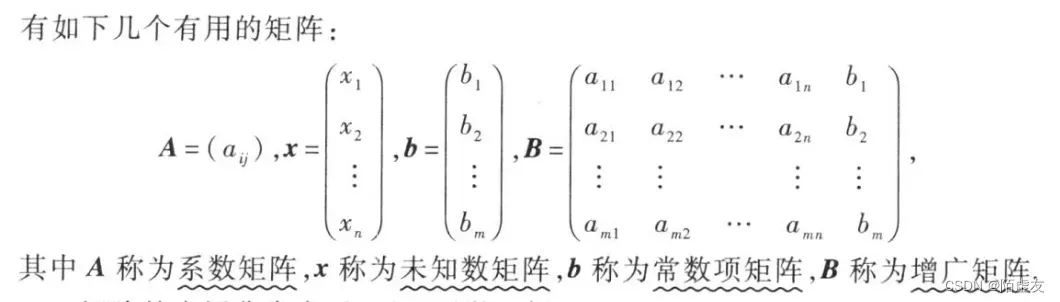
矩阵中的每个数被称为元素,简称为元,数
位于矩阵A的第i行第j列,称为矩阵A 的(i,j)元,m
n矩阵A也记作
行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵.n阶矩阵A也记作A
行矩阵:只有一行的矩阵,又称行向量
列矩阵:只有一列的矩阵,又称列向量
零矩阵:元素都是零的矩阵称为零矩阵,记作O,注意不同型的零矩阵是不同的.
对角矩阵:从左上角到右下角的直线(叫做对角线)以外的元素都是0.这种方阵称为对角矩阵,简称对角阵.对角阵也记作
![]()
2.2 矩阵的运算
2.2.1 矩阵的加法
定义2 设有两个m×n阵A=()和B=(
),那么矩阵A与B的和记做A+B,规定为
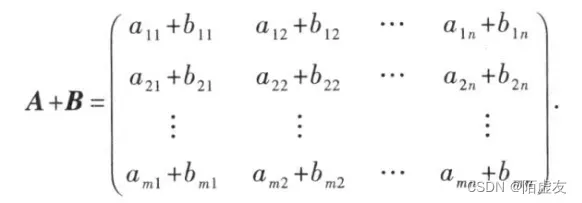
矩阵加法满足下列运算规律
(设A,B,C都是m×n矩阵):
- A+B=B+A;
- (A+B)+C=A+(B+C).
设矩阵A=(),记-A=(-
),-A称为矩阵A的负矩阵,显然有 A+(-A)=O
由此规定矩阵的减法为 A-B=A+(-B)
2.2.2 矩阵的乘法
数乘矩阵满足下列运算规律(设A、B为m×n矩阵,λ、μ为数):
- (λμ)A=λ(μA);
- (λ+μ)A=λA+μA;
- λ(A+B)=λA+λB.
矩阵加法与数乘矩阵统称为矩阵的线性运算.
矩阵之间的乘法:

矩阵的乘法不满足交换律,但仍满足下列结合律和分配律(假设运算都是可行的):
- (AB)C=A(BC);
- λ(AB)=(λA)B=A(λB)(其中λ为数);
- A(B+C)=AB+AC,(B+C)A=BA+CA.
例题


2.2.3 矩阵的转置
- 定义5 把矩阵A的行换成同序数的列得到一个新矩阵,叫做A的转置矩阵,记作
.
矩阵的转置也是一种运算,满足下述运算规律(假设运算都是可行的):
=A;
- (A+B)T=
+
;
- (λA)T=λ
;
- (AB)T=
;
2.3 方阵的行列式
- 定义6 由n阶方阵A的元素所构成的行列式(各元素的位置不变),称为方阵A的行列式,记作detA或|A|.
由A确定︳A︳的这个运算满足下述运算规律(设A、B为n阶方阵,λ为数):
- |
|=|A|;
- λA=
|A|;
- |AB︳=|A||B|.
伴随矩阵:

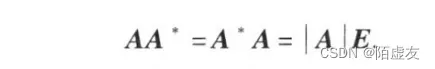
证明:
2.4 逆矩阵(重点)
2.4.1 逆矩阵的定义
- 定义7 对于n阶矩阵A,如果有一个n阶矩阵B,使AB=BA=E,则说矩阵A是可逆的,并把矩阵B称为A的逆矩阵,简称逆阵.
如果矩阵A是可逆的,那么A的逆矩阵是惟一的.这是因为:若B、C都是A的逆矩阵,则有B=BE=B(AC)=(BA)C=EC=C,所以A的逆矩阵是惟一的.A的逆矩阵记作.即若AB=BA=E,则B=
.
- 定理1 若矩阵A可逆,则|A|≠0.

定理2 证明:
- 推论 若AB=E(或BA=E),则B=

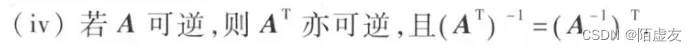 2.4.2 求逆矩阵
2.4.2 求逆矩阵
我们在这里先只介绍一种求逆矩阵的方法 :由伴随矩阵求逆矩阵,后续我们讲到矩阵的初等行变换时会介绍另外的求法
由定理2我们知道
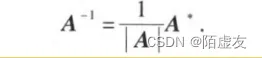
我们可以由此公式很容易便得出矩阵的逆矩阵,并不需要进行思维较为复杂的矩阵行变换(另一种求逆矩阵的方法),但是这种计算方式计算量大,不适合阶数较大的方阵,一般适用于特殊形式的矩阵计算,会节省我们做题的时间
例题
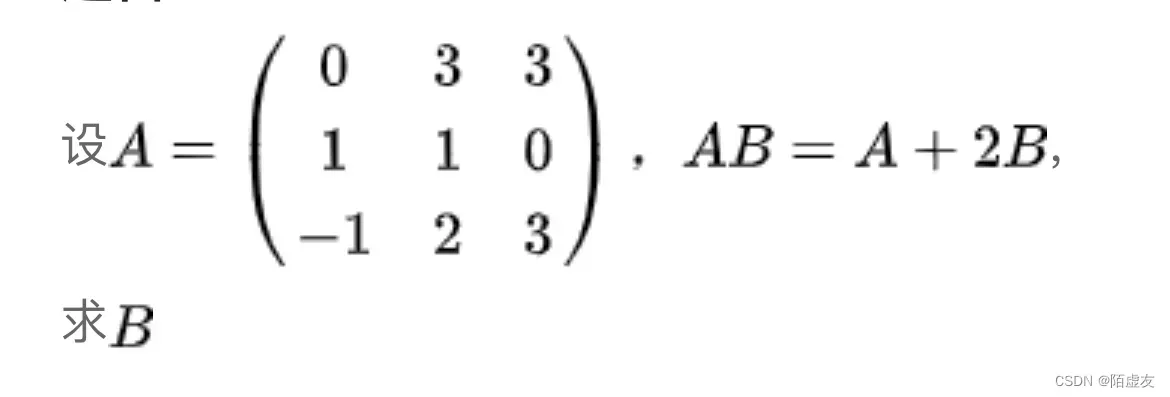
 2.5 克拉默法则
2.5 克拉默法则
- 克拉默法则 如果线性方程组的系数矩阵A的行列式不等于零,那么,方程组有惟一解
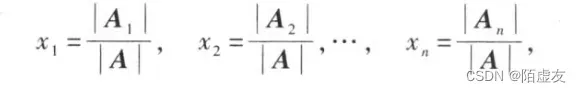

看例题是最快理解概念的方式

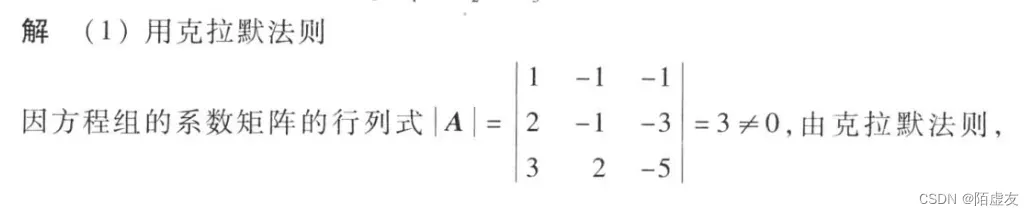

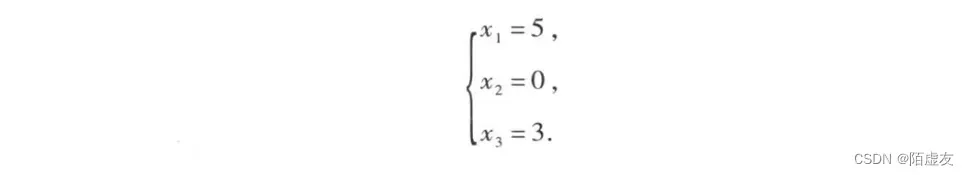
三、矩阵的初等变换与线性方程组
3.1 矩阵的初等行变换

矩阵之间的等价关系具有下列性质:
- 反身性A~A;
- 对称性若A~B,则B~A;
- 传递性若A~B,B~C,则A~C.
3.2 行阶梯型矩阵
定义
- 可画出一条阶梯线,线的下方全是0
- 每个台阶只有一行
- 阶梯线的竖线后面是非零行的第一个非零元素
进一步,若A是行阶梯形矩阵,并且还满足:
- 非零行的首非零元为1;
- 首非零元所在的列的其他元均为0,
则称A为行最简形矩阵.
如图示:(行最简型矩阵)
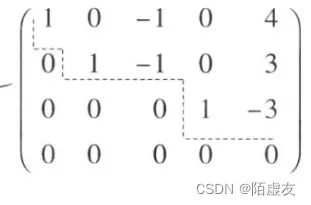
标准形:对行最简形矩阵再施以初等列变换,可变成一种形状更简单的矩阵,称为标准形.例如:
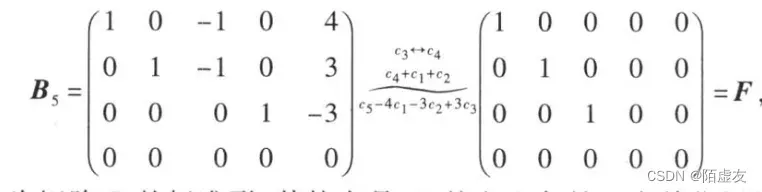 矩阵的初等变换是矩阵的一种最基本的运算,为探讨它的应用,需要研究它的性质,下面介绍它的一个最基本的性质.
矩阵的初等变换是矩阵的一种最基本的运算,为探讨它的应用,需要研究它的性质,下面介绍它的一个最基本的性质.
- 定义3 由单位矩阵E经过一次初等变换得到的矩阵称为初等矩阵.
由定义3,我们可以给出初等矩阵的一些性质(选择题可能会出相关概念题)
- 性质1 设A是一个m×n矩阵,对A施行一次初等行变换,相当于在A的左边乘相应的m阶初等矩阵;对A施行一次初等列变换,相当于在A的右边乘相应的n阶初等矩阵.
- 性质2 方阵A可逆的充分必要条件是存在有限个初等矩阵Pn,P2,…,Pl,使A=P1P2…Pn.
- 推论 方阵A可逆的充分必要条件是
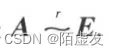
3.3 初等行变换求逆矩阵
学习了矩阵的初等行变换后 ,我们就可以用此种方法求矩阵的逆矩阵了
例题


3.4 矩阵的秩
- 定义4 在m×n矩阵A中,任取k行与k列(k≤m,k≤n),位于这些行列交叉处的
个元素,不改变它们在A中所处的位置次序而得的k阶行列式,称为矩阵A的k阶子式.
- 引理 设
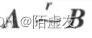 则A与B中非零子式的最高阶数相等.
则A与B中非零子式的最高阶数相等. - 定义5 设在矩阵A中有一个不等于0的r阶子式D,且所有r+1阶子式(如果存在的话)全等于0,那么D称为矩阵A的最高阶非零子式,数r称为矩阵A的秩,记作R(A).并规定零矩阵的秩等于0.
- 定理2 若A~B,则R(A)=R(B).
简单来说,矩阵的秩就等于行阶梯型矩阵非零行的个数
例题
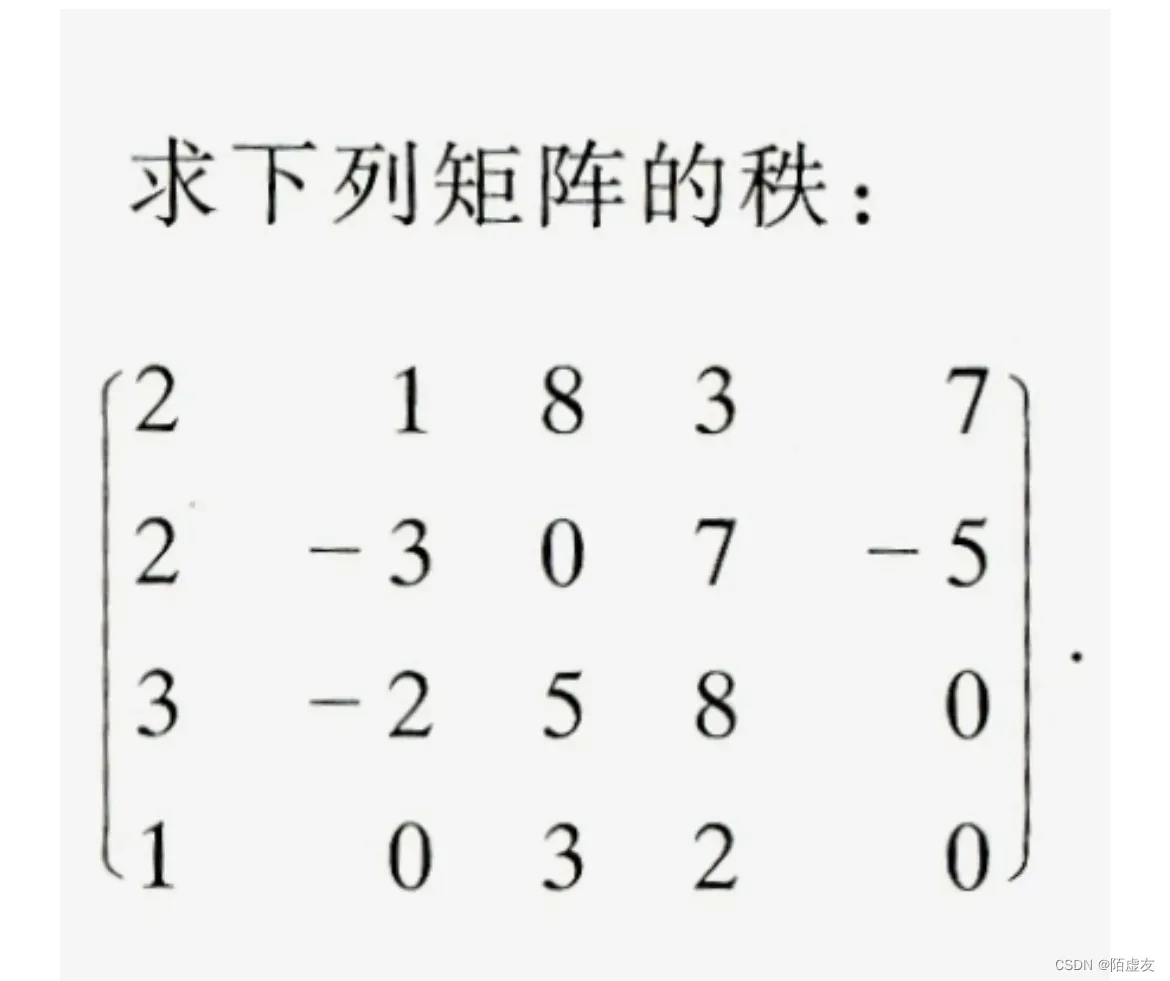

矩阵秩的一些性质

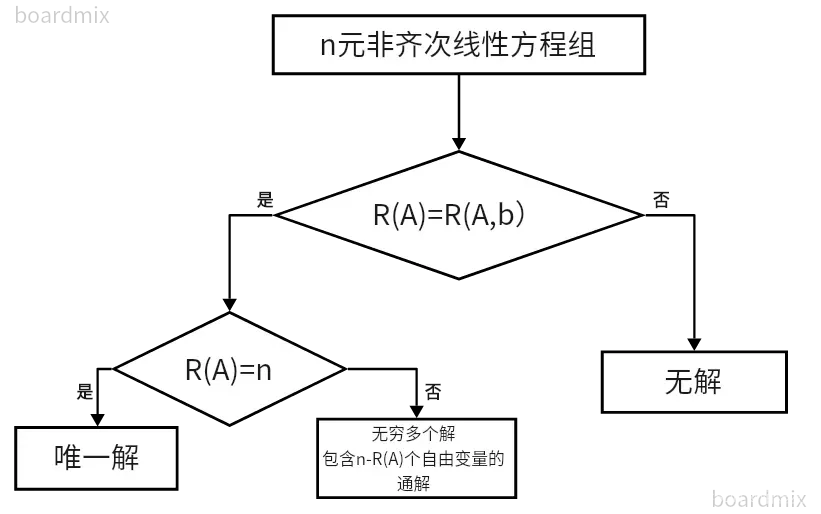
3.5 线性方程组的解

定理3 n元线性方程组Ax=b
- 无解的充分必要条件是R(A)<R(A,b);
- 有惟一解的充分必要条件是R(A)=R(A,b)=n;
- 有无限多解的充分必要条件是R(A)=R(A,b)<n.
其对应的齐次线性方程组Ax=0,有非零解的充分必要条件是R(A)<n
以下是一个帮助我们理解的流程图
例题


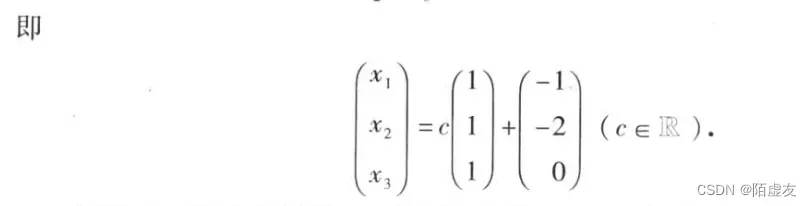
四、向量的线性相关性
4.1 向量组及其线性组合
- 定义1 n个有次序的数a1,a2,…,an所组成的数组称为n维向量,这n个数称为该向量的n个分量,第i个数ai称为第i个分量.
n维向量可写成一行,也可写成一列.

若干个同维数的列向量(或同维数的行向量)所组成的集合叫做向量组.
- 定义2 给定向量组A:a1,a2,…,am,对于任何一组实数k1,k2,…,km,表达式k1a1+k2a2+…+kmam称为向量组A的一个线性组合,k1,k2,…,km称为这个线性组合的系数.
- 给定向量组A:a1,a2,…,am和向量b,如果存在一组数λ1,λ2,…,λm,使b=λ1a1+λ2a2+…+λmam,则向量b是向量组A的线性组合,这时称向量b能由向量组A线性表示.
- 定理1 向量b能由向量组A:a1,a2,…,am线性表示的充分必要条件是矩阵A=(a1,a2,…,am)的秩等于矩阵B=(a,1a2,…,am,b)的秩.
- 定义3 设有两个向量组A:a1,a2,…,am及B:b1,b2,…,bl,若B组中的每个向量都能由向量组A线性表示,则称向量组B能由向量组A线性表示.若向量组A与向量组B能相互线性表示,则称这两个向量组等价.
- 定理2 向量组B:b1,b2,…,bl能由向量组A:a1,a2,…,am线性表示的充分必要条件是矩阵A=(a1,a2,…,am)的秩等于矩阵(A,B)=(a1,…,am,b1,…,bl)的秩,即R(A)=R(A,B).
- 推论 向量组A:a1,a2,…,am与向量组B:b1,b2,…,bl等价的充分必要条件是R(A)=R(B)=R(A,B),其中A和B是向量组A和B所构成的矩阵.
例题



- 定理3 设向量组B:b1,b2,…,bl能由向量组A:a1,a2,…,am线性表示,则R(b1,b2,…,bl)≤R(a1,a2,…,am)
4.2 向量组的线性相关性

 例题
例题


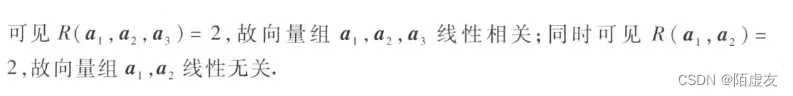
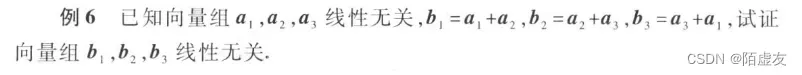

4.3 课后题
这章的概念实在太多了,光会概念可不行,考试得要会做题,我们接下来用例题的方式来理解







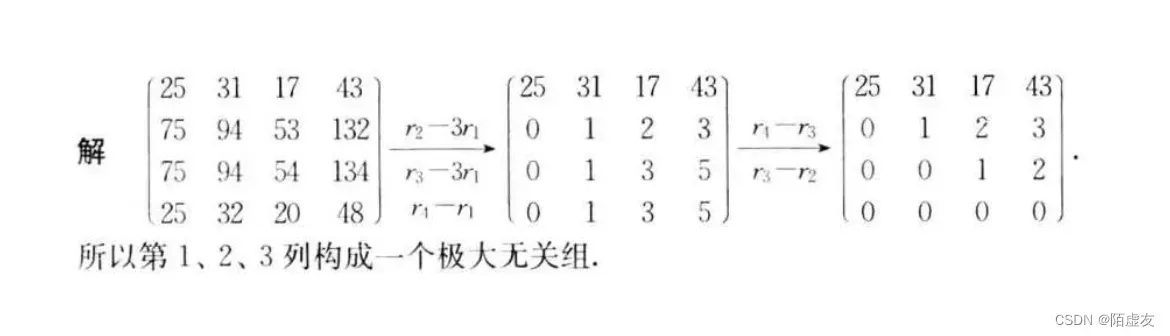

5、相似矩阵及二次型
本章偷偷懒~~,省略了一些内容
5.1 方阵的特征值与特征向量
定义6 设A是n阶矩阵,如果数λ和n维非零列向量x使关系式
Ax=λx(1)成立,
那么,这样的数λ称为矩阵A的特征值,非零向量x称为A的对应于特征值λ的特征向量.
(1)式也可写成(A-λE)x=0,这是n个未知数n个方程的齐次线性方程组,它有非零解的充分必要条件是系数行列式|A-λE︳=0,
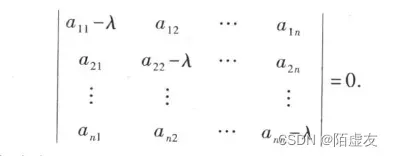
上式是以λ为未知数的一元n次方程,称为矩阵A的特征方程,其左端︳A-λE︳是λ的n次多项式,记作f(λ),称为矩阵A的特征多项式.显然,A的特征值就是特征方程的解.
例题
![]()

5.2 相似矩阵
5.2.1 相似矩阵定义
- 定理3 若n阶矩阵A与B相似,则A与B的特征多项式相同,从而A与B的特征值亦相同.
定理3 证明:
若n阶矩阵A和B相似,则A的多项式与B的多项式
相似
5.2.2 对角化
对n阶矩阵A,寻求相似变换矩阵P,使P-1AP=Λ为对角矩阵,这就称为把矩阵A对角化.
例题




看到这里的朋友给个点赞吧

版权声明:本文为博主作者:陌虚友原创文章,版权归属原作者,如果侵权,请联系我们删除!
原文链接:https://blog.csdn.net/m0_73406058/article/details/135163098