
当你觉的自己不行时,你就走到斑马线上,这样你就会成为一个行人
一、交换排序
1.冒泡排序 BubbleSort
1.1 基本思想
1.2 实现原理
1.3 代码实现
1.4 冒泡排序的特性总结
2.快速排序 QuickSort
2.1 基本思想
2.2 递归实现
2.2.1 hoare版
2.2.2 前后指针版本
2.3 快速排序优化
2.3.1 随机数选key
2.3.2 三数取中选key
2.3.3 递归到小的子区间使用插入排序
2.4 非递归实现
2.5 快速排序的特性总结
二、完结撒❀
前言:
所谓交换排序,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特点是(以升序为例):将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀-正文开始-❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–
一、冒泡排序
对于冒泡这个初学者必学的排序,我想大家应该都不陌生,现在我们以排升序为例再简单学习回顾一下,为下面快速排序做铺垫。
1.1 基本思想
冒泡排序是从头开始让两个相邻位置的数进行大小比较,不符合升序的将两者进行交换,再继续向后比较两个数据大小,反复执行一轮上述操作,便可以将数组中最大数据排到队尾,再从头进行一轮上述操作便可以将数组中第二大的数据排到数组中倒数第二个位置,反复执行n-1次即可完成排序(n为数据总个数)
1.2 实现原理
在数组arr[n]中,开始将数组arr[0]与arr[1]进行大小比较,若arr[1]<arr[0]就将两者数值进行交换后继续进行arr[1]与arr[2]的大小比较,若arr[1]>arr[0]就继续向后进行arr[1]与arr[2]的大小比较,直到比较到arr[n-1]为止,这时arr[n-1]便是数组中最大的值,再执行一轮上述操作便可以将数组中第二大的数值存放到arr[n-2]当中,反复执行n-1次便完成数组的总排序
动态图解:

1.3 代码实现
//冒泡排序
void BubbleSort(int* a, int n)
{
assert(a);
for (int t = 1; t < n; t++)
{
int exchang = 0;//优化
for (int i = 0; i < n - t; i++)//优化
{
if (a[i] > a[i + 1])
{
int tmp = a[i];
a[i] = a[i + 1];
a[i + 1] = tmp;
exchang = 1;
}
}
if (exchang == 0)
{
break;
}
}
}
代码中对冒泡排序进行了两处优化,大家认真品味,加深理解。
1.4 冒泡排序的特性总结
1. 冒泡排序是一种非常容易理解的排序
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:稳定
2.快速排序
2.1 基本思想
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码(数组下标)将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止
2.2 递归实现
2.2.1 Hoare版
Hoare版就是Hoare大佬自己创作的最原始的快速排序。
根据上述基本思想我们可以发现快速排序递归实现与二叉树的前序遍历规则非常像,在代码的实现中我们就可参照二叉树前序递归实现快速排序代码的递归框架。
我们先认真观察下面快速排序的动态图解:
 上面1动态图解表示的是快速排序的一次单趟过程:
上面1动态图解表示的是快速排序的一次单趟过程:
以数组左边第一个值为key,R先向左走找小于key的数就停下来(5),接着L向右走找大于key的值就停下来(7),再将L和R对应位置数值进行交换,接着R继续向左走找小于key的值(4),找到后停下L向右走找大于key的值(9),之后停下再将两数值进行交换,继续重复上述操作直到L与R相遇,L与R相遇之后再将相遇下标对应的值与key下标对应的值进行交换,这样就完成了一次单趟快速排序,此时key的右边都为小于key的值,右边都是大于key的值。
快速排序单趟实现代码:
void Swap(int* p, int* q)
{
int tmp = *p;
*p = *q;
*q = tmp;
}
//快速排序(单趟)
void PartSort(int* a, int left, int right)
{
assert(a);
int keyi = left;
while (left < right)
{
while (left<right && a[right] >= a[keyi])
{
--right;
}
while (left<right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[right], &a[left]);
}
Swap(&a[left], &a[keyi]);
keyi = left;
}
这里强调一下,一趟快速排序开始必须先让R往左边走,保证在最后L与R相遇时下标对应的值小于key下标对应的值
那么我们单趟排序便实现完成,下面就要开始展开研究递归问题。
递归就分为:1.递归子问题 2.最终子问题
我们对一串数组进行一次单趟的快速排序之后,数组并没有完全实现有序,还要“分割”key左右两边对其再分别进行快速排序,再将“分割”的一段再按照快排后key的位置在进行分割再进行单趟排序,直到分割为一个数据的时候就可以返回,也就是L = R,最后也可能为空
如图所示:
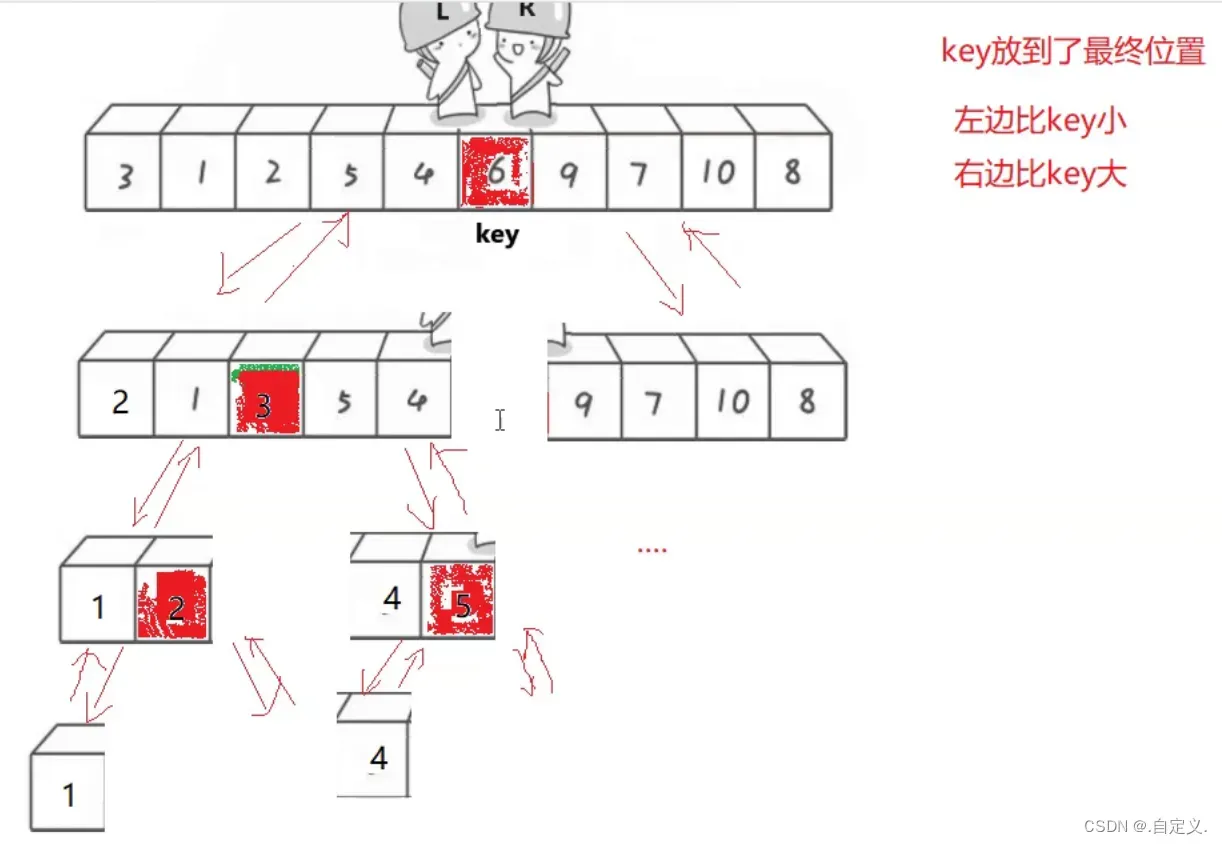
递归顺序我们就可以按照二叉树前序进行设计,所以代码实现如下:
//快速排序(霍尔递归)
void QuickSort1(int* a, int left, int right)
{
assert(a);
//递归子条件 区间只有一个值或者不存在
if (left >= right)
{
return;
}
int begin = left;
int end = right;
int keyi = left;
while (left < right)
{
while (left < right && a[right] >= a[keyi])
{
--right;
}
while (left < right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[right], &a[left]);
}
Swap(&a[left], &a[keyi]);
keyi = left;
//区间划分[begin,key-1] [key] [key+1,end]
QuickSort1(a, begin, keyi - 1);
QuickSort1(a, keyi + 1, end);
}
我们可以试着用递归实现一组排序并画出递归展开图,有助于更深刻的理解递归。
2.2.2 前后指针版本
在Hoare大佬之后,有人在快速排序上增加其他实现玩法,前后指针实现快速排序就是其中u一种
大家可以先看一下下面递归图解进行学习:

可以看到,快慢指针最后也实现了key之前都小于key对应的值,key之后都大于key对应的值的效果
起初prev指向数组的开头,key也指向这个位置,cur指向prev前一个位置
判断cur指向的值是否大于key所指向的值
1.如果cur指向的值小于key指向的值,让prev加1向前移动一个位置,再交换cur和prev所指向的值,再将cur加1向前移动一个位置。
2.如果cur指向的值大于key指向的值,让cur+1向前移动一个位置。
持续循环判断上述逻辑,直到cur越界,最后再将prev和key所指向位置的对应值进行交换。
上面所讲的便是前后指针版实现一次单趟的整体逻辑。大家可以去尝试自行动手实现一下
前后指针单趟排完的效果与Hoare版的效果是一样的,所以我们只需要镶套上递归逻辑实现递归即可
代码如下:
//快速排序(双指针递归)
void QuickSort2(int* a, int left, int right)
{
assert(a);
if (left >= right)//递归终止条件
{
return;
}
int prev = left;
int keyi = left;
int cur = left + 1;
//增加代码可读性
int begin = left;
int end = right;
while (cur <= right)
{
if (a[cur] < a[keyi] && ++prev != cur)//这里排除了当prev与cur位置相同时的情况,在同一位置时不用交换
Swap(&a[prev], &a[cur]);
++cur;
}
Swap(&a[keyi], &a[prev]);
keyi = prev;
QuickSort2(a, begin, keyi - 1);//left
QuickSort2(a, keyi + 1,end);//right
}
2.3 快速排序优化
这里我们先来计算一下快速排序的时间复杂度
对于上面所讲述的情况是以key最终取到的是中间位置然后在进行递归为例
相当于每次递归单趟排序只排好了数组中的一个数据
那么其时间复杂度就为O(N*logN)
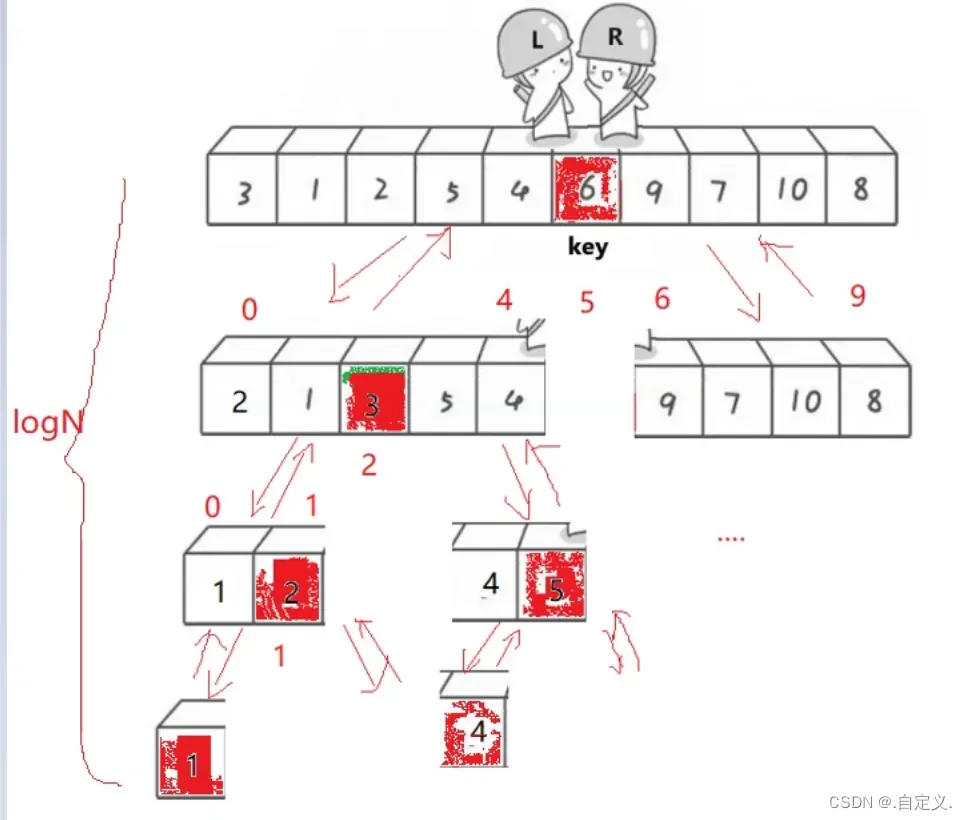
而时间复杂度都是以最坏情况下计算的,那么快速排序在什么情况下是最坏的呢?
根据递归情况,当数组本身为有序的时候,对于快速排序来说的最坏的情况
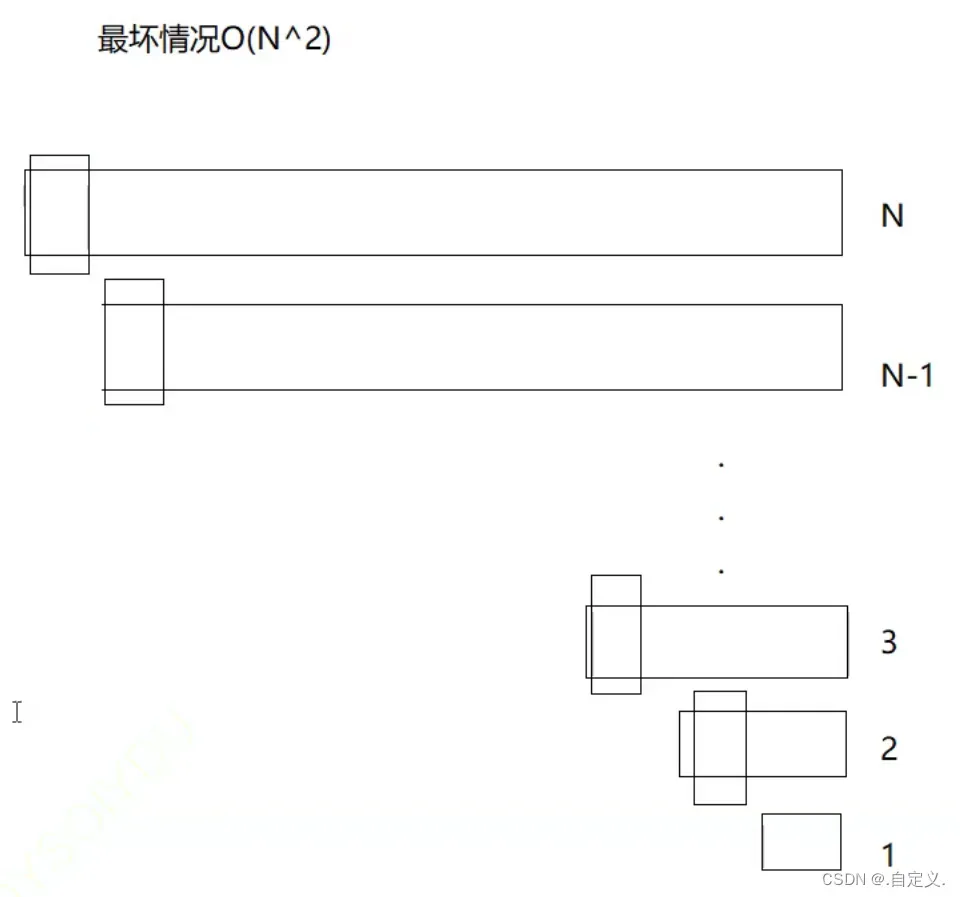
此时每次都是以头部数据为key进行排序,那么递归深度为N,所以此时其时间复杂度为O(N^2)
有些同学可能就会好奇:“时间复杂度为N^2为什么效率会那么快”
因为每次进行排序,要排的数据本身就为有序概率是很低的,也可以说快速排序的适应性比较强,所以排序一般效率都非常快
但是有序出现的概率小并不代表不会出现,并且如果出现数据过多并且还是有序的情况下,不仅效率低下而且还可能会造成栈溢出,那么我应该怎么对其进行优化来解决这个问题呢?
2.3.1 随机数选key
上面所述问题的根本原因就是因为我们每次进行单趟排序的时候所选的key都是头部所指的位置数据,因为是有序数组,所以头部数据一定是数组中最小或最大的数据,这就造成遇到有序数据效率骤然下降
所以我们可以在每次递归都改变头部位置所指向的数据再进行单趟排序。
大家可以先看一下实现代码:
void Swap(int* p, int* q)
{
int tmp = *p;
*p = *q;
*q = tmp;
}
//快速排序(霍尔递归)
void QuickSort1(int* a, int left, int right)
{
assert(a);
//递归子条件 区间只有一个值或者不存在
if (left >= right)
{
return;
}
int begin = left;
int end = right;
//打破最坏情况有序---生成随机数
int randi = rand() % (left - right);
randi += left;
Swap(&a[randi], &a[left]);
int keyi = left;
while (left < right)
{
while (left < right && a[right] >= a[keyi])
{
--right;
}
while (left < right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[right], &a[left]);
}
Swap(&a[left], &a[keyi]);
keyi = left;
//[begin,key-1] [key] [key+1,end]
QuickSort1(a, begin, keyi - 1);
QuickSort1(a, keyi + 1, end);
}
我们生成随机数来做为数组下标进行操作
那么生成的随机数肯定是需要在所要进行排序的数组范围内,我们将生成的随机数余上排序数组的队尾下标与队头下标之差,之后在加上对头下标,随机数的范围就一定是在所要排序的数组内。
再将随机数下标所对应的值与对头数据进行交换,那么key所对应的值就不是原来数组对头的值,这样就解决了有序数组的问题。
但这中也只是大大降低了在有序数组中key所对应的值为最值得概率,当随机数等于队尾与对头之差时余上便等于0,此时key指向得还是对头的值,所以有人觉得这种方法不妥,于是又有了下面一种方法。
2.3.2 三数取中选key
这里得三数是指队头数据,中间数据(队尾下标与对头下标之和除2)和队尾数据
在这三个数据中选出大小为中间的值做key,这样key对应的值就一定不是其数组中的最值了
实现代码:
int GetMidi(int* a,int left,int right)
{
int midi = (left + right) / 2;
if (a[midi] > a[left])
{
if (a[midi] < a[right])
{
return midi;
}
else //(a[midi]>a[right])
{
if (a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
}
else //a[midi] < a[left]
{
if (a[midi] > a[right])
{
return midi;
}
else
{
if (a[left] > a[right])
{
return right;
}
else
{
return left;
}
}
}
}
//快速排序(霍尔递归)
void QuickSort1(int* a, int left, int right)
{
assert(a);
//递归子条件 区间只有一个值或者不存在
if (left >= right)
{
return;
}
int begin = left;
int end = right;
//三数取中
int midi = GetMidi(a, left, right);
Swap(&a[midi], &a[left]);
int keyi = left;
while (left < right)
{
while (left < right && a[right] >= a[keyi])
{
--right;
}
while (left < right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[right], &a[left]);
}
Swap(&a[left], &a[keyi]);
keyi = left;
//[begin,key-1] [key] [key+1,end]
QuickSort1(a, begin, keyi - 1);
QuickSort1(a, keyi + 1, end);
}
}
这样就可以完全避免最坏情况的出现
2.3.3 递归到小的子区间使用插入排序
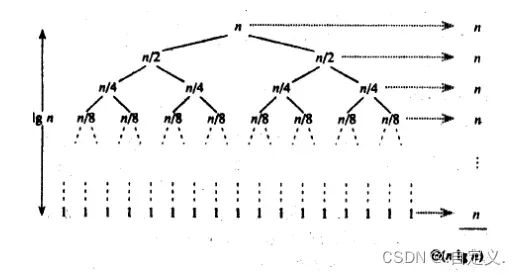
因为我们递归实现形成的是二叉树结构,而对于二叉树我们看下图:
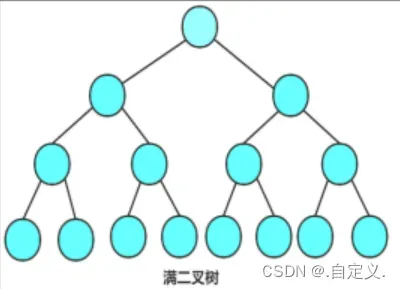
二叉树递归最后一层递归开辟栈帧的空间次数是占总递归的50%,而倒数第二层占总空间的25%,所以最后的两次递归消耗都已经占总消耗的75%左右
而对于我们快排也是如此,在递归到最后两层只剩下部分数据需要排序的话我们可以不选择使用快排,我们可以选择使用插入排序来进行解决
代码实现:
int GetMidi(int* a,int left,int right)
{
int midi = (left + right) / 2;
if (a[midi] > a[left])
{
if (a[midi] < a[right])
{
return midi;
}
else //(a[midi]>a[right])
{
if (a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
}
else //a[midi] < a[left]
{
if (a[midi] > a[right])
{
return midi;
}
else
{
if (a[left] > a[right])
{
return right;
}
else
{
return left;
}
}
}
}
//快速排序(霍尔递归)
void QuickSort1(int* a, int left, int right)
{
assert(a);
//递归子条件 区间只有一个值或者不存在
if (left >= right)
{
return;
}
//小区间可以走插入,能减少90%的递归空间消耗
if (right - left + 1 < 10)
{
InsertSort(a + left, right - left + 1);//a+left保证从每个递归区间进行排序
}
else
{
int begin = left;
int end = right;
//打破最坏情况有序---生成随机数
/*int randi = rand() % (left - right);
randi += left;
Swap(&a[randi], &a[left]);*/
//三数取中
int midi = GetMidi(a, left, right);
Swap(&a[midi], &a[left]);
int keyi = left;
while (left < right)
{
while (left < right && a[right] >= a[keyi])
{
--right;
}
while (left < right && a[left] <= a[keyi])
{
++left;
}
Swap(&a[right], &a[left]);
}
Swap(&a[left], &a[keyi]);
keyi = left;
//[begin,key-1] [key] [key+1,end]
QuickSort1(a, begin, keyi - 1);
QuickSort1(a, keyi + 1, end);
}
}
这样就会减少大部分空间的开辟,减少消耗,减小空间复杂度
2.4 非递归实现
上面我们所讲述的都是利用递归进行实现快排的方法,那么大家可以想想如何不用递归来进行逻辑实现
非递归实现快排要用到栈来实现
我们想一想快排递归是如何实现,我们要怎样用栈来进行存储
递归中我们所传的参数有数组指针,队头下标和队尾下标,数组指针肯定不需要我们再往栈中进行存储,所以我们要想实现非递归我们就需要把每次递归所传的参数进行存储,将每次所传的参数进行单趟排序即可完成快速排序。
动态图解:

栈实现的是先进后出,上面动态图解中先往栈中入右子区间再入左区间那么实现逻辑就是先排左边再排右边,与二叉树前序遍历相符,当区间为1或是为空的时候便不在进行入栈操作最后实现效果与递归实现一样。
实现代码:
//利用栈 实现非递归快排
void QuickSortNonR(int* a, int left, int right)
{
assert(a);
ST st;
STInit(&st);
STPush(&st, right);
STPush(&st, left);
while (!STEmpty(&st))
{
int begin = STTop(&st);
STPop(&st);
int end = STTop(&st);
STPop(&st);
int prev = begin;
int keyi = begin;
int cur = begin + 1;
//增加代码可读性
while (cur <= end)
{
if (a[cur] < a[keyi] && ++prev != cur)//在同一位置不用交换
Swap(&a[prev], &a[cur]);
++cur;
}
Swap(&a[keyi], &a[prev]);
keyi = prev;
//[begin]~[keyi-1] [keyi+1]~[end]
if (begin < keyi - 1)
{
STPush(&st, keyi - 1);
STPush(&st,begin);
}
if (keyi + 1 < end)
{
STPush(&st, end);
STPush(&st, keyi+1);
}
}
STDestory(&st);
}
上面代码中含有栈的函数,不知道的可以去我将的栈与队列的博客中进行复制学习:栈与队列
2.5 快速排序的特性总结
1.快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
2. 时间复杂度:O(N*logN)(优化后)
3. 空间复杂度:O(logN)
4. 稳定性:不稳定
二、完结撒❀
如果以上内容对你有帮助不妨点赞支持一下,以后还会分享更多编程知识,我们一起进步。
最后我想讲的是,据说点赞的都能找到漂亮女朋友❤

版权声明:本文为博主作者:.自定义.原创文章,版权归属原作者,如果侵权,请联系我们删除!
