傅里叶级数系数的完整详细算法

傅里叶级数系数的完整详细算法

一、三角函数相关公式和定积分

在分析傅里叶级数之前，一定要先熟悉三角函数的相关公式，以及三角函数的积分。

1、两角和公式：

sin(α+β) = sin(α) * cos(β) + cos(α) * sin(β)

sin(α–β) = sin(α) * cos(β) – cos(α) * sin(β)

cos(α+β) = cos(α) * cos(β) – sin(α) * sin(β)

cos(α–β) = cos(α) * cos(β) + sin(α) * sin(β)

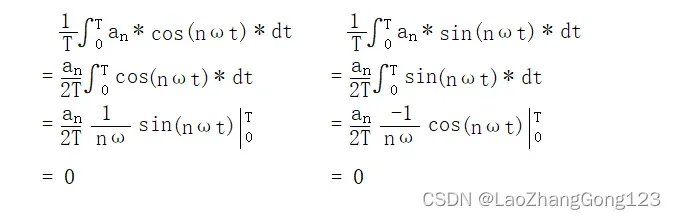
2、积化和差公式：

sin(α) * cos(β) = [sin(α+β) + sin(α–β)] / 2

cos(α) * sin(β) = [sin(α+β) – sin(α–β)] / 2

cos(α) * cos(β) = [cos(α+β) + cos(α–β)] / 2

sin(α) * sin(β) = [cos(α–β) – cos(α+β)] / 2

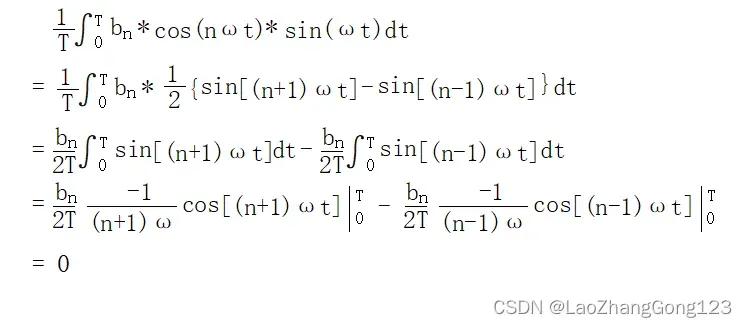
二、傅立叶级数：

1、傅立叶级数展开公式

对于一个周期为T的函数f(t)，可以将其展开为以下的形式：

2、傅立叶级数的系数计算

1)、对傅里叶级数展开公式两边同时积分，可以计算到a0

2)、对傅里叶级数展开公式两边同时乘以cos(kωt)积分，然后等式两边同时求积分，就可以计算到ak，注意：k>=1。

3)、对傅里叶级数展开公式两边同时乘以sin(kωt)积分，然后等式两边同时求积分，就可以计算到bk，注意：k>=1。

三、傅立叶级数滤波的原理：

如果我们将上式中，去掉省略号后面的项目，就可以得到新的函数表达式，如下：

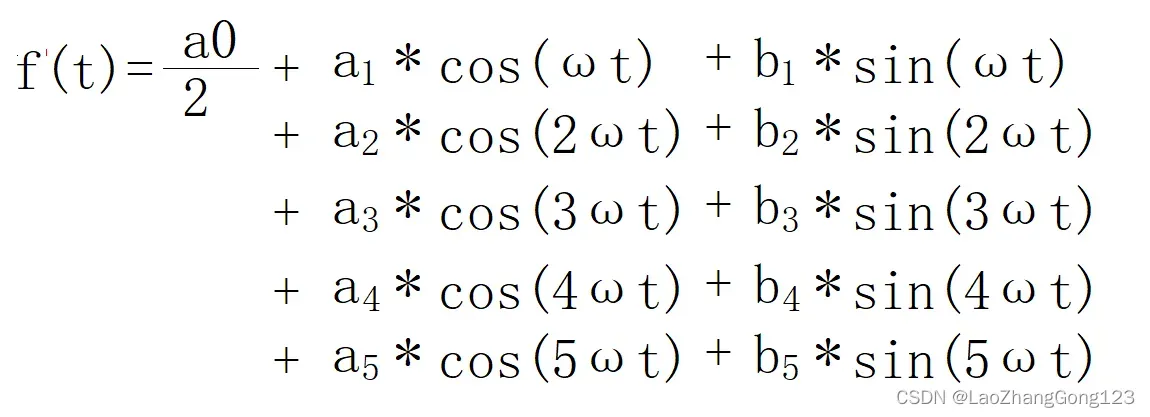
这就是去掉5次以上谐波后的新函数，也就是我们求的滤波函数。

在实际使用中，我们通常会使用“傅里叶级数”进行数字滤波，其原理如下:

已知一维数组MyArray[]是周期数f(t)的一部分数据，且在MyArray[]数据中至少有一个周期数据是函数f(t)的最小周期数据。

因此，我们可以将MyArray[]当作周期函数f(t)来对待，就可以使用傅里叶级数来表示。

在傅里叶级数展开前，需要先计算傅里叶级数的系数:

a0

a1,a2,…,ak

b1,b2,…,bk

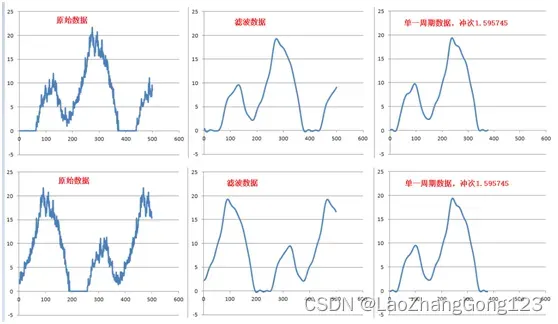
通过傅里叶级数展开式，我们发现，如果去掉“高次谐波的数据”，得到数据波形，就会更加平滑，且更接近“理想波形”。

四、滤波效果图