【C++】红黑树

红黑树 

目录

a. 红黑树的概念

红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或

Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路

径会比其他路径长出俩倍，因而是接近平衡的

b. 红黑树的性质

1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的，则它的两个孩子结点是黑色的
4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点
5. 空结点都是黑色的

c. 红黑树的实现

（一）红黑树节点的构建

代码

	enum Colour
{
	RED,
	BLACK
};

template<class K, class V>
struct RBTreeNode
{
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;
	pair<K, V> _kv;
	Colour _col;

	RBTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _kv(kv)
		, _col(RED)  //默认为红节点，对于性质四，黑节点数不好控制，先默认红节点，后期再变颜色
	{}
};

（二）红黑树的插入

实现思路

如果插入的是第一个节点（即根节点），由于性质二，我们需要把它变成黑色

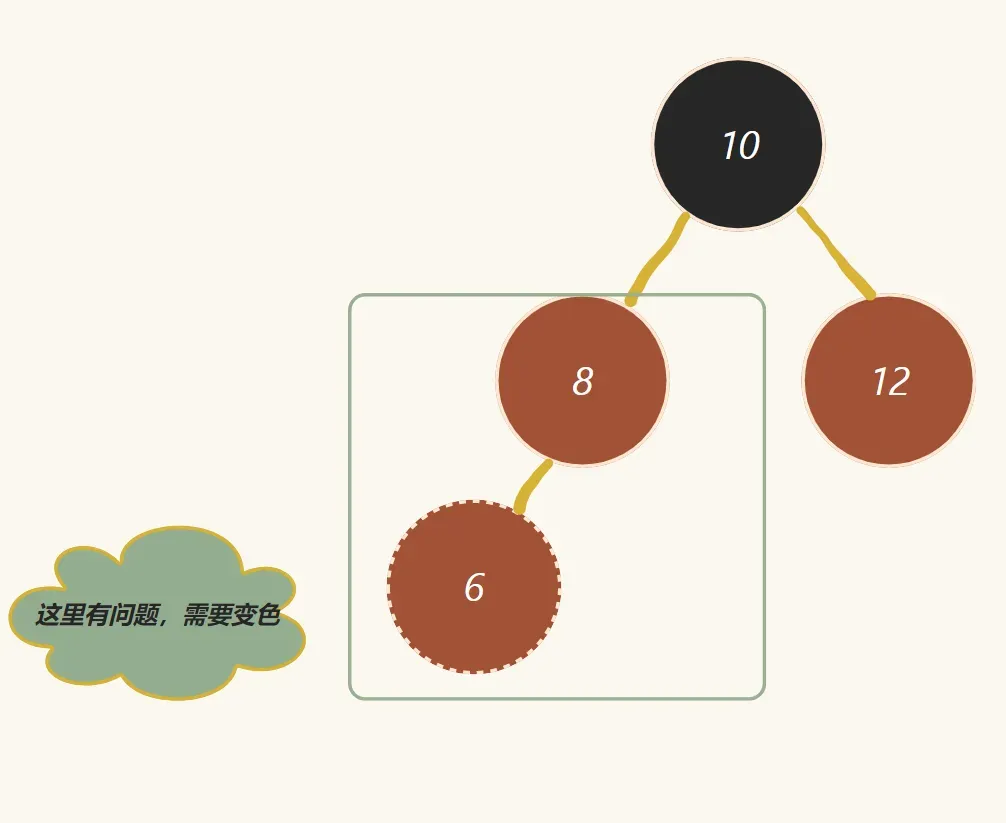
除了上述情况，还有一种可能需要变色（回到性质三）

如图：

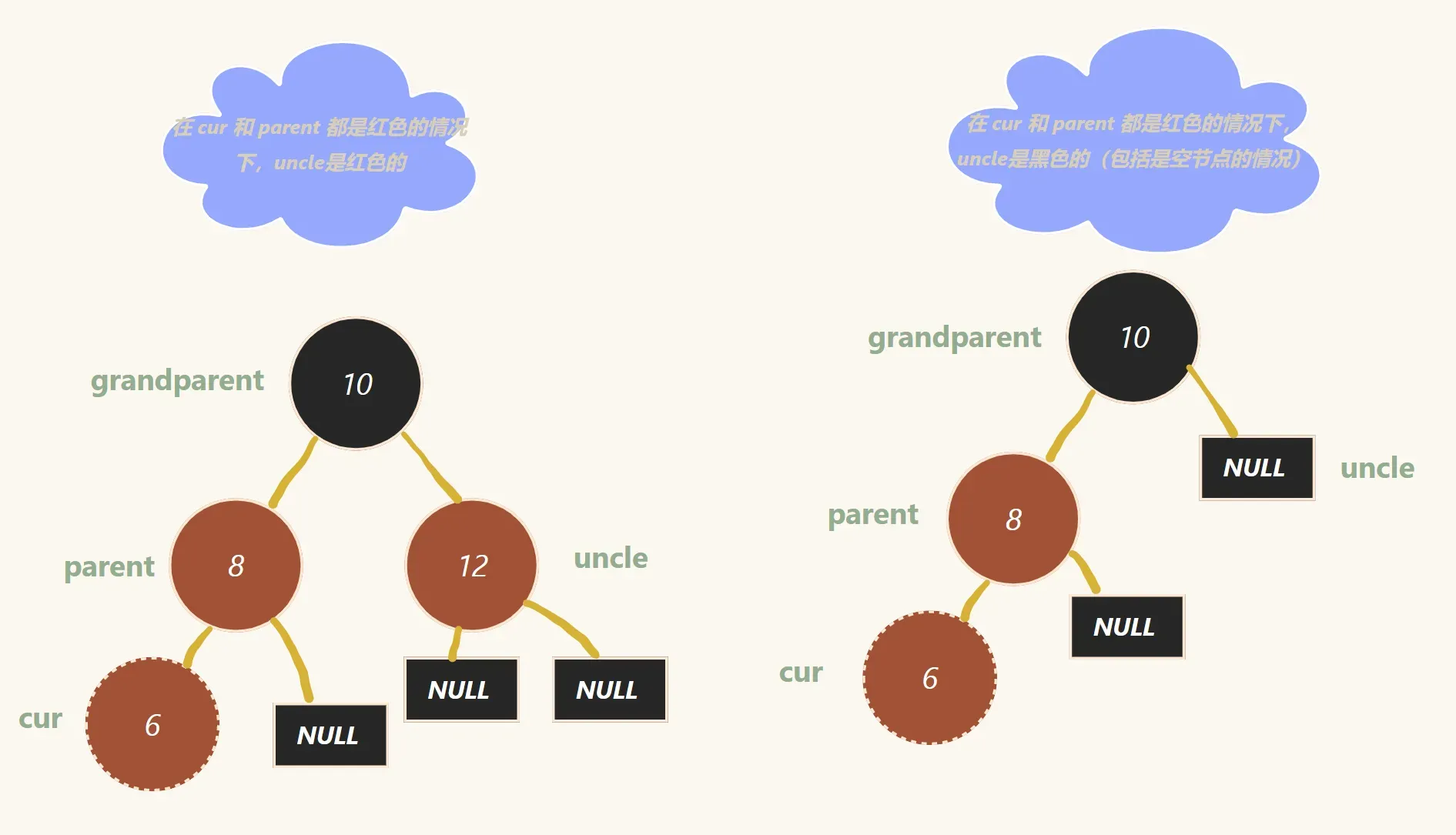
而面对这种情况，也分不同的做法

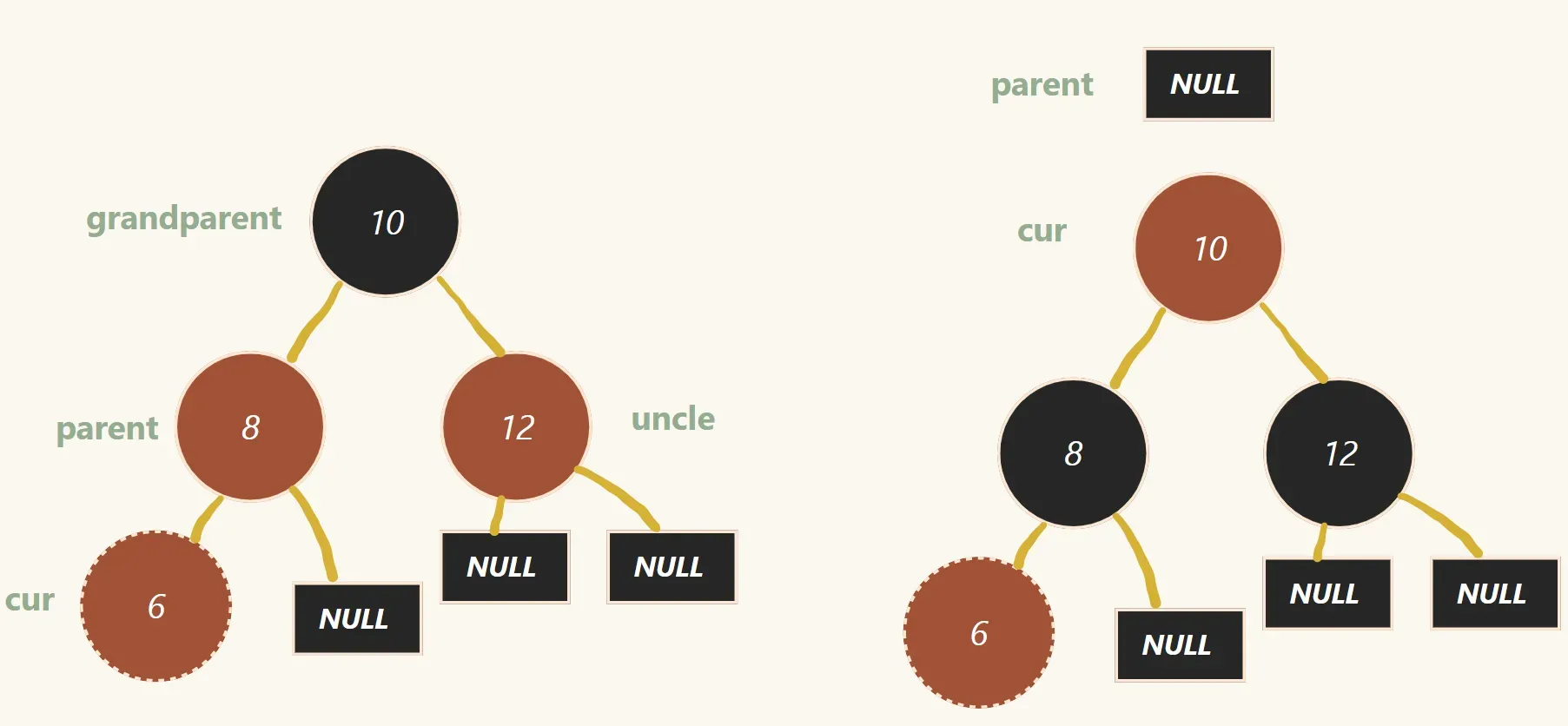
对于第一种情况（左图）：

做法是把 parent 变成黑色的 ， grandparent 变成红色的 ，uncle 变成黑色的 ，

然后 cur = grandparent , parent = cur->_parent , grandparent = parent->_parent ，uncle 也有变节点 ，直到不满足两个红节点连在一起的前提 或者 是 parent 为空（循环结束的条件）

注意：

根节点的颜色可能会在过程中更改（如上述右图），一定要在最后改回成黑色

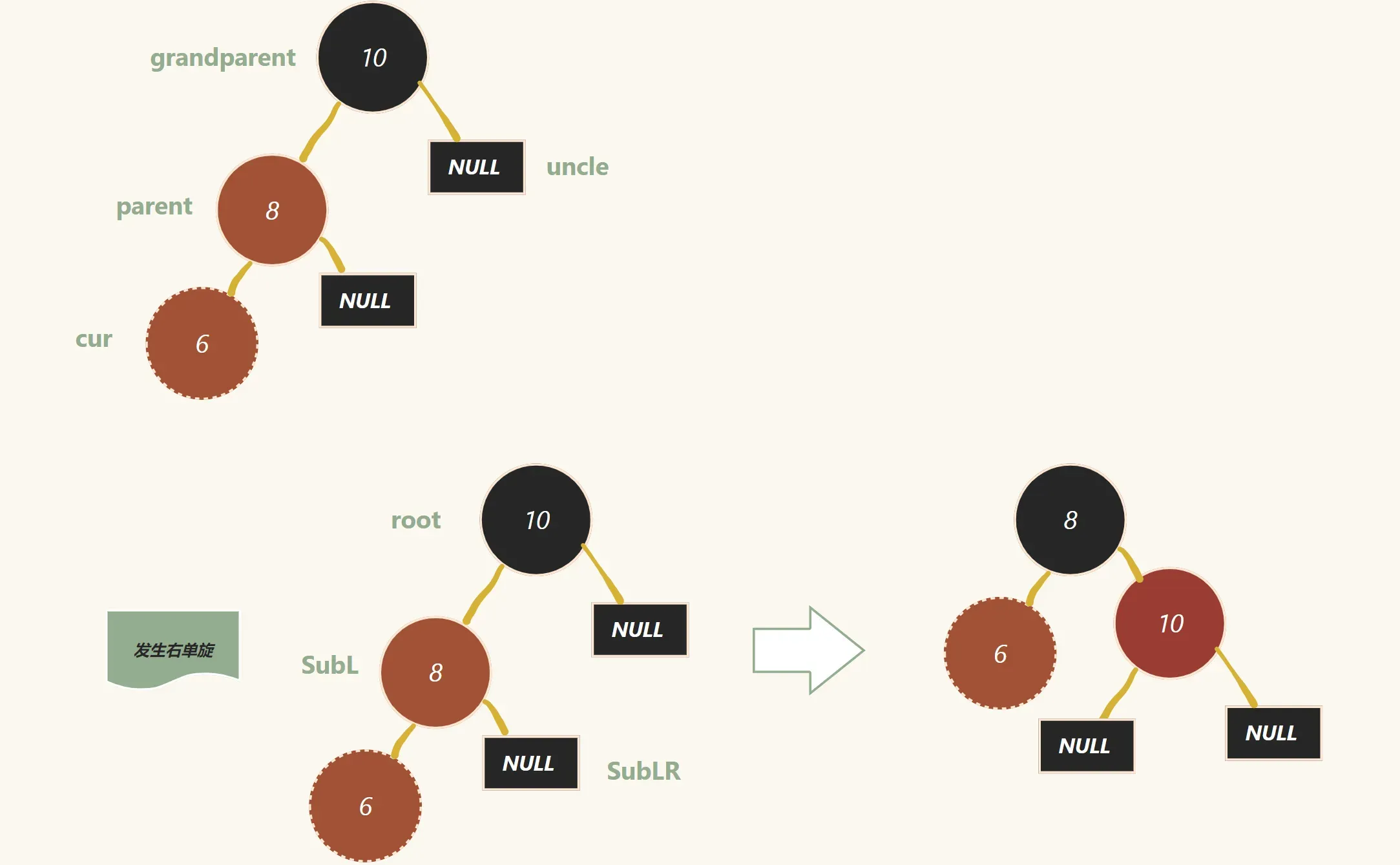
对于第二种情况：

parent 变成黑色 ， grandparent 变成红色 ，再发生旋转（跟 AVL树 的旋转情况一样），完成 break即可

 代码

	enum Colour
{
	RED,
	BLACK
};

template<class K, class V>
struct RBTreeNode
{
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;
	pair<K, V> _kv;
	Colour _col;

	RBTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _kv(kv)
		, _col(RED)
	{}
};


template<class K, class V>
class RBTree
{
	typedef RBTreeNode<K, V> Node;
public:
	bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_col = BLACK;
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;

		while (cur)
		{
			if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

		cur = new Node(kv);
		cur->_parent = parent;
		if (parent->_kv.first > cur->_kv.first)
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		while (parent && parent->_col == RED)
		{
			Node* grandparent = parent->_parent;
			if (parent == grandparent->_left)
			{
				Node* uncle = grandparent->_right;
				if (uncle && uncle->_col == RED)
				{
					parent->_col = BLACK;
					uncle->_col = BLACK;
					grandparent->_col = RED;

					cur = grandparent;
					parent = cur->_parent;
				}
				else
				{
					if (grandparent->_left == parent && parent->_left == cur)
					{
						RotateR(grandparent);
					}
					else
					{
						RotateLR(grandparent);
					}
					parent->_col = BLACK;
					grandparent->_col = RED;
					
					cur = grandparent;
					parent = cur->_parent;
				}
			}
			else
			{
				Node* uncle = grandparent->_left;
					if (uncle && uncle->_col == RED)
					{
						parent->_col = BLACK;
						uncle->_col = BLACK;
						grandparent->_col = RED;

						cur = grandparent;
						parent = cur->_parent;
					}
					else
					{
						
						if (grandparent->_right == parent && parent->_right == cur)
						{
							RotateL(grandparent);
						}
						else
						{
							RotateRL(grandparent);
						}
						parent->_col = BLACK;
						grandparent->_col = RED;
						
						cur = grandparent;
						parent = cur->_parent;
					}
			}
		}
		_root->_col = BLACK;
		return true;
	}
	void InOder()
	{
		_InOder(_root);
	}
	bool IsBalance()
	{

		return  _IsBalance(_root, 0);
	}
	~RBTree()
	{
		Destory(_root);
		_root = nullptr;
	}
private:
	bool _IsBalance(Node* root,int MaxBlack) //验证是否是红黑树
	{
		if (root == nullptr)
		{
			cout << MaxBlack + 1 << endl;
			return true;
		}
		Node* parent = root->_parent;
		if (_root->_col == RED)
		{
			return false;
		}
		if (root->_col == RED && parent && parent->_col == RED)
		{
			return false;
		}
		if (root->_col == BLACK)
		{
			++MaxBlack;
		}
		return _IsBalance(root->_left, MaxBlack) && _IsBalance(root->_right, MaxBlack);
	}
	void RotateR(Node* root)
	{
		Node* SubL = root->_left;
		Node* SubLR = SubL->_right;
		if (root == _root)
		{
			_root = SubL;
		}
		else
		{
			Node* parent = root->_parent;
			if (parent->_left == root)
			{
				parent->_left = SubL;
			}
			else
			{
				parent->_right = SubL;
			}
		}
		root->_left = SubLR;
		SubL->_right = root;
		SubL->_parent = root->_parent;
		root->_parent = SubL;
	}
	void RotateL(Node* root)
	{
		Node* SubR = root->_right;
		Node* SunRL = SubR->_left;
		if (root == _root)
		{
			_root = SubR;
		}
		else
		{
			Node* parent = root->_parent;
			if (parent->_left == root)
			{
				parent->_left = SubR;
			}
			else
			{
				parent->_right = SubR;
			}
		}
		root->_right = SunRL;
		SubR->_left = root;
		SubR->_parent = root->_parent;
		root->_parent = SubR;
	}
	void RotateLR(Node* root)
	{
		Node* SubL = root->_left;
		Node* SubLR = SubL->_right;
		RotateL(SubL);
		RotateR(root);
	}
	void RotateRL(Node* root)
	{
		Node* SubR = root->_right;
		Node* SubRL = SubR->_left;
		RotateR(SubR);
		RotateL(root);
	}
	void _InOder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}
		_InOder(root->_left);
		cout << root->_kv.first << " " << root->_col << endl;
		_InOder(root->_right);
	}
	void Destory(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}
		Destory(root->_left);
		Destory(root->_right);
		delete root;
	}
	Node* _root = nullptr;
};