一、相关性模型简介
相关性模型并不是指一个具体的模型,而是一类模型,这一类模型用来判断变量之间是否具有相关性。一般来说,分析两个变量之间是否具有相关性,我们根据数据服从的分布和数据所具有的特点选择使用pearson(皮尔逊)相关系数和spearman(斯皮尔曼)等级相关系数;分析两组变量,每组变量都有多个指标的时候,无论是pearson相关系数还是spearman等级相关系数都无能为力,所以又要介绍一个新的典型相关分析来解决这个问题。
二、适用赛题
显而易见,这些相关性模型适用于探究变量之间的关系,帮助了解它们是否存在相关性,以及相关性的强度和方向。
三、模型流程
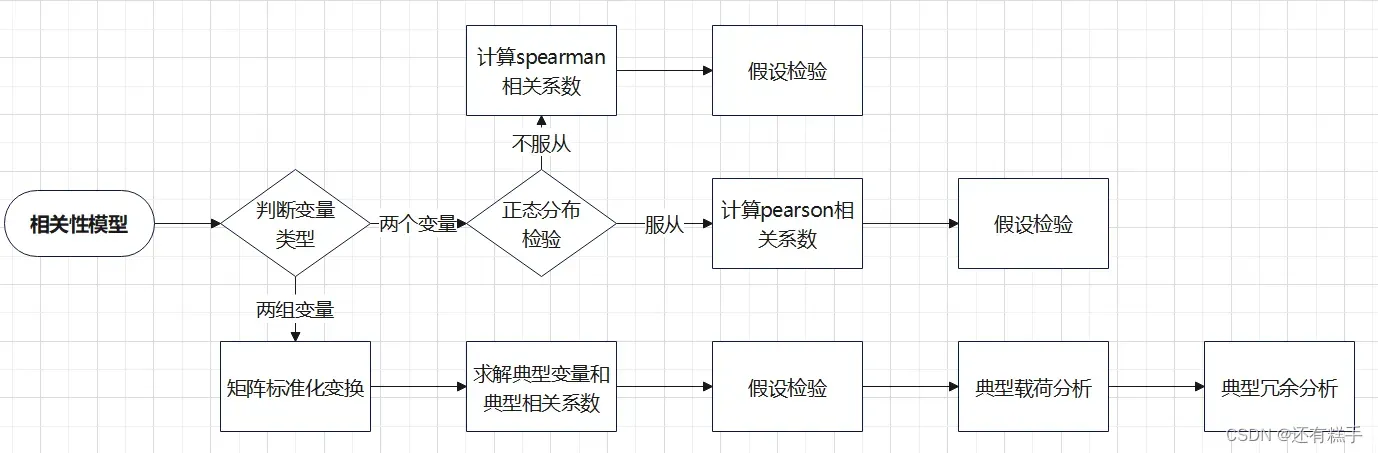
四、流程分析
因为整个流程包含三个模型,所以会以pearson相关系数,spearman等级相关系数,典型相关分析的顺序来讲解。
注:本篇存在大量的概率论与数理统计的知识,这里并不对其中出现的知识、定理等作概念说明和详细证明
1.pearson相关系数
可以从流程图看到,应用pearson相关系数条件还是比较苛刻的。首先得是两个变量之间,其次这两个变量的数据还要服从正态分布。其实应用pearson相关系数的条件还不止,后面会全部介绍。
①正态分布检验
为什么要正态分布检验?
- 第一,实验数据通常假设是成对的来自于正态分布的总体。因为我们在求pearson相关系数以后,通常还会用t检验之类的方法来进行皮尔逊相关系数检验,而t检验是基于数据呈正态分布的假设的
- 第二,实验数据之间的差距不能太大。皮尔逊相关性系数受异常值的影响比较大
- 第三,每组样本之间是独立抽样的。构造t统计量时需要用到
Ⅰ正态分布JB检验(大样本 n > 30)
雅克-贝拉检验(Jarque-Bera test)

这是原理,但是在MATLAB中,代码很简单
注:有些地方正态分布峰度为0,MATLAB中是3
skewness(x) % 偏度
kurtosis(x) % 峰度可以用这两句查询数据的偏度和峰度
MATLAB中进行JB检验的语法:
[h, p] = jbtest(x, alpha);当输出h等于1时,表示拒绝原假设;h等于0则代表不能拒绝原假设。alpha就是显著性水平,一般取0.05, 此时置信水平为1 – 0.05 = 0.95。x就是我们要检验的随机变量,注意这里的x只能是向量。
ⅡShapiro-wilk检验(小样本 3 ≤ n ≤ 50)
Shapiro-wilk 夏皮洛-威尔克检验

此操作一般在SPSS软件上进行。
②计算相关系数
pearson相关系数的原理在概率论课本上有,无论是总体还是样本。这里给出MATLAB中如何求
R = corrcoef(A) % 返回A的相关系数的矩阵,其中A的列表示随机变量(指标),行表示观测值(样本)
R = corrcoef(A, B) % 返回两个随机变量A和B (两个向量) 之间的系数关于pearson相关系数的总结
- 如果两个变量本身就是线性的关系,那么pearson相关系数绝对值大的就是相关性强,小的就是相关性弱
- 在不确定两个变量是什么关系的情况下,即使算出pearson相关系数,发现很大,也不能说明那两个变量线性相关,甚至不能说它们相关,我们一定要画出散点图来看才行
③假设检验
事实上,比起相关系数的大小,我们往往更关注的是显著性(假设检验)
原理这里不再给出,证明过于复杂。
这里用更好的方法:p值判断法
一行代码得到p值
[R, P] = corrcoef(test);R返回的是相关系数表,P返回的是对应于每个相关系数的p值
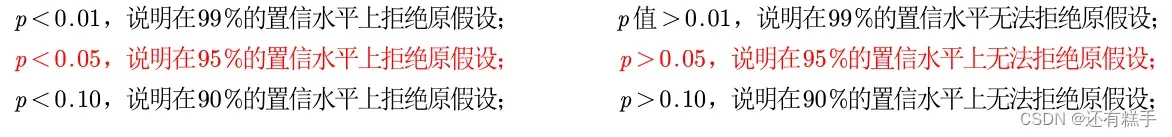
注:拒绝原假设意味着pearson相关系数显著的异于0
2.spearman等级相关系数
pearson相关系数不能用,就使用spearman等级相关系数。鉴于pearson相关系数中已经介绍过正态分布检验,这里不在重复。
①计算相关系数

注:如果有的数值相同,则将它们所在的位置取算术平均。
举个例子:
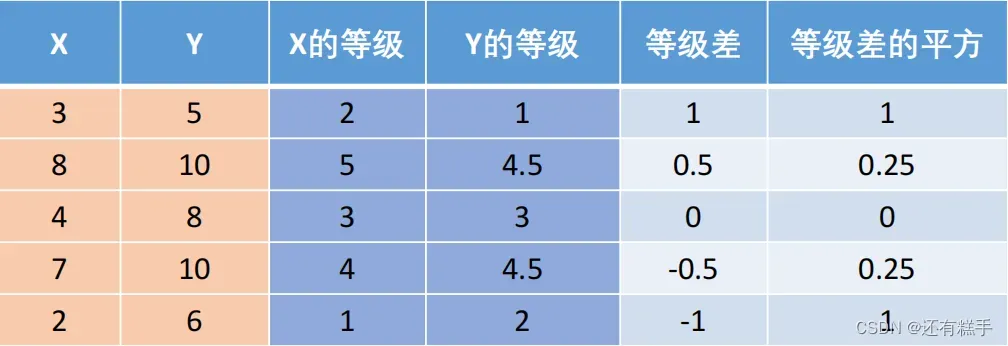
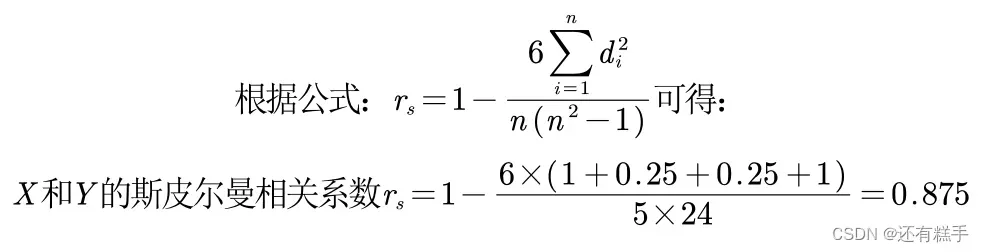
在MATLAB中,代码也是很简单
coeff = corr(X, Y, 'type', 'Spearman'); % 这里的X和Y必须是列向量
coeff = corr(x, 'type', 'Spearman'); % 这时计算X矩阵各列之间的spearman相关系数②假设检验
Ⅰ小样本情况(n ≤ 30)
直接查临界值表即可
|
n |
单尾检验的显著水平 |
|||
|
.05 |
.025 |
.01 |
.005 |
|
|
双尾检验的显著水平 |
||||
|
.10 |
.05 |
.02 |
.01 |
|
|
4 |
1.000 |
|||
5 |
0.900 |
1.000 |
1.000 |
|
6 |
0.829 |
0.886 |
0.943 |
1.000 |
|
7 |
0.714 |
0.786 |
0.893 |
0.929 |
|
8 |
0.643 |
0.738 |
0.833 |
0.881 |
|
9 |
0.600 |
0.700 |
0.783 |
0.833 |
|
10 |
0.564 |
0.648 |
0.745 |
0.794 |
|
11 |
0.536 |
0.618 |
0.709 |
0.755 |
|
12 |
0.503 |
0.587 |
0.671 |
0.727 |
|
13 |
0.484 |
0.560 |
0.648 |
0.703 |
|
14 |
0.464 |
0.538 |
0.622 |
0.675 |
|
15 |
0.443 |
0.521 |
0.604 |
0.654 |
|
16 |
0.429 |
0.503 |
0.582 |
0.635 |
|
17 |
0.414 |
0.485 |
0.566 |
0.615 |
|
18 |
0.401 |
0.472 |
0.550 |
0.600 |
|
19 |
0.391 |
0.460 |
0.535 |
0.584 |
|
20 |
0.380 |
0.447 |
0.520 |
0.570 |
|
21 |
0.370 |
0.435 |
0.508 |
0.556 |
|
22 |
0.361 |
0.425 |
0.496 |
0.544 |
|
23 |
0.353 |
0.415 |
0.486 |
0.532 |
|
24 |
0.344 |
0.406 |
0.476 |
0.521 |
|
25 |
0.337 |
0.398 |
0.466 |
0.511 |
|
26 |
0.331 |
0.390 |
0.457 |
0.501 |
|
27 |
0.324 |
0.382 |
0.448 |
0.491 |
|
28 |
0.317 |
0.375 |
0.440 |
0.483 |
|
29 |
0.312 |
0.368 |
0.433 |
0.475 |
|
30 |
0.306 |
0.362 |
0.425 |
0.467 |
|
35 |
0.283 |
0.335 |
0.394 |
0.433 |
|
40 |
0.264 |
0.313 |
0.368 |
0.405 |
|
45 |
0.248 |
0.294 |
0.347 |
0.382 |
|
50 |
0.235 |
0.279 |
0.329 |
0.363 |
|
60 |
0.214 |
0.255 |
0.300 |
0.331 |
|
70 |
0.190 |
0.235 |
0.278 |
0.307 |
|
80 |
0.185 |
0.220 |
0.260 |
0.287 |
|
90 |
0.174 |
0.207 |
0.245 |
0.271 |
|
100 |
0.165 |
0.197 |
0.233 |
0.257 |
注:样本相关系数r必须大于等于表中的临界值,才能得出显著的结论。
Ⅱ大样本情况
依旧是选择更好用的p值检验法
[R, P] = corr(test, 'type', 'Spearman'); % 直接给出相关系数和p值这里和p值和pearson相关系数假设检验那里的p值解释相同。
3.pearson相关系数和spearman等级相关系数选择
- 连续数据,正态分布,线性关系,用pearson相关系数是最恰当,当然用spearman等级相关系数也可以,就是效率没有pearson相关系数高
- 上述任一条件不满足,就用spearman等级相关系数,不能用pearson相关系数
- 两个定序数据之间也用spearman等级相关系数,不能用pearson相关系数
定序数据是指仅仅反映观测对象等级、顺序关系的数据,是由定序尺度计量形成的,表现为类别,可以进行排序,属于品质数据。
例如:优、良、差;我们可以用1表示差、2表示良、3表示优,但请注意,用2除以1得出的2并不代表任何含义。定序数据最重要的意义代表了- -组数据中的某种逻辑顺序。
注:斯皮尔曼相关系数的适用条件比皮尔逊相关系数要广,只要数据满足单调关系(例如线性函数、指数函数、对数函数等)就能够使用。
4.典型相关分析
声明:对于典型相关分析,其中原理、证明过于复杂,本篇不作涉及,只介绍得出结果的流程。
基本思想
典型相关分析由Hotelling提出,其基本思想和主成分分析非常相似。首先在每组变量中找出变量的线性组合,使得两组的线性组合之间具有最大的相关系数。然后选取和最初挑选的这对线性组合不相关的线性组合,使其配对,并选取相关系数最大的一对,如此继续下去,直到两组变量之间的相关性被提取完毕为此。被选出的线性组合配对称为典型变量,它们的相关系数称为典型相关系数。典型相关系数度量了这两组变量之间联系的强度。
①矩阵标准化变换
矩阵的标准化变换属于线性代数的知识,这里介绍为什么要对矩阵进行标准化变化的操作
- 典型相关分析涉及多个变量,不同的变量往往具有不同的量纲及不同的数量级别。在进行典型相关分析时,由于典型变量是原始变量的线性组合,具有不同量纲变量的线性组合显然失去了实际意义
- 其次,不同的数量级别会导致“以大吃小”,即数量级别小的变量的影响会被忽略,从而影响了分析结果的合理性
- 因此,为了消除量纲和数量级别的影响,必须对数据先做标准化变换处理,然后再做典型相关分析
②求解
再看过第一步之后肯定是一头雾水,矩阵是哪里来的?这里对典型相关分析中的变量做一些介绍

规定有
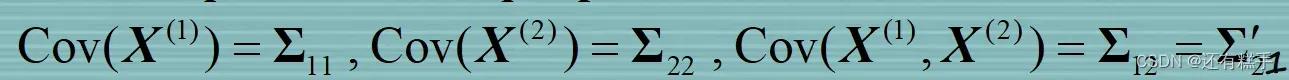
第一步的矩阵标准化就是对这四个矩阵进行操作
这里以一组数据为例子
康复俱乐部对20名中年人测量了三个生理指标:体重(x1),腰围(x2),脉搏(x3);三个训练指标:引体向上次数(y1),起坐次数(y2),跳跃次数(y3)。分析生理指标与训练指标的相关性。
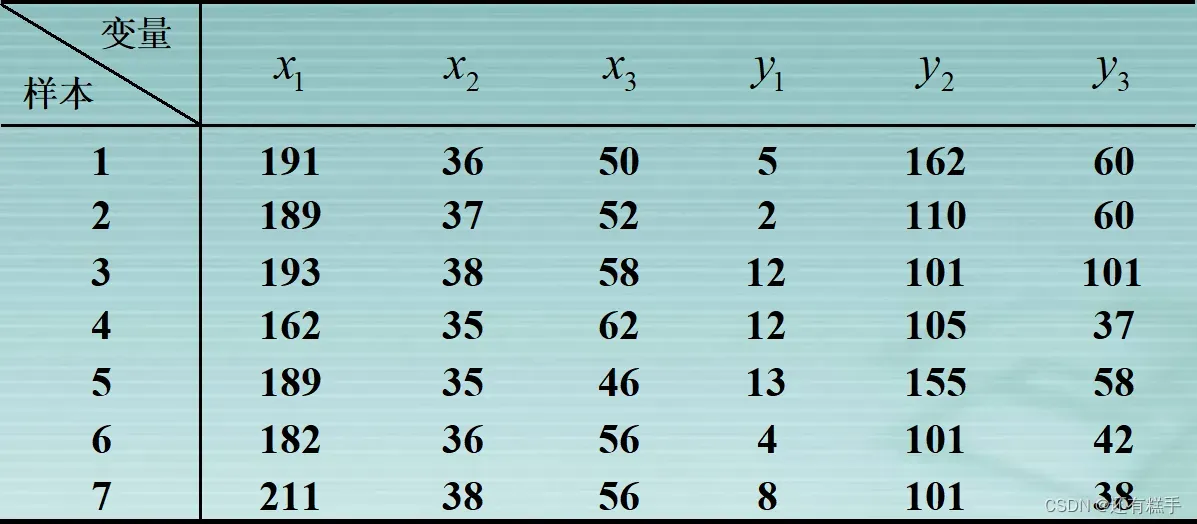
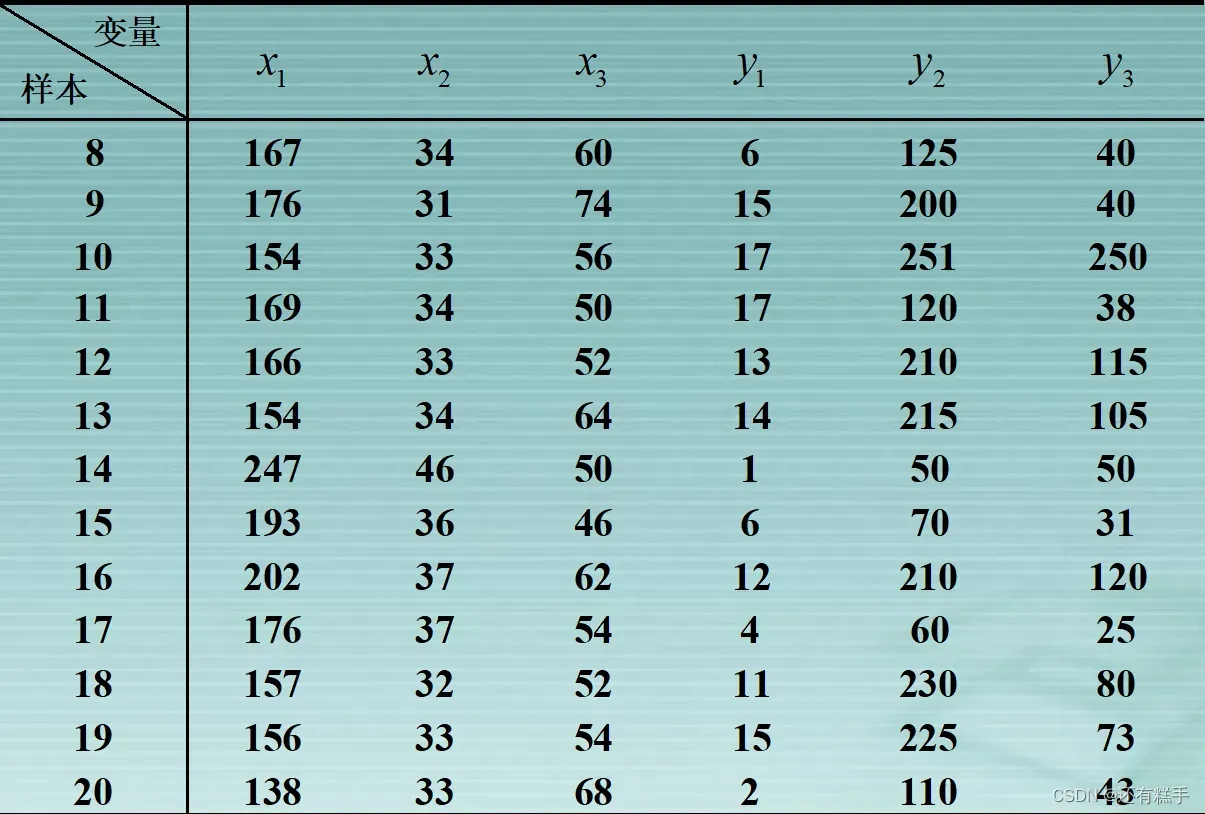
根据数据可得


在标准化之后,矩阵用R表示

设置A和B
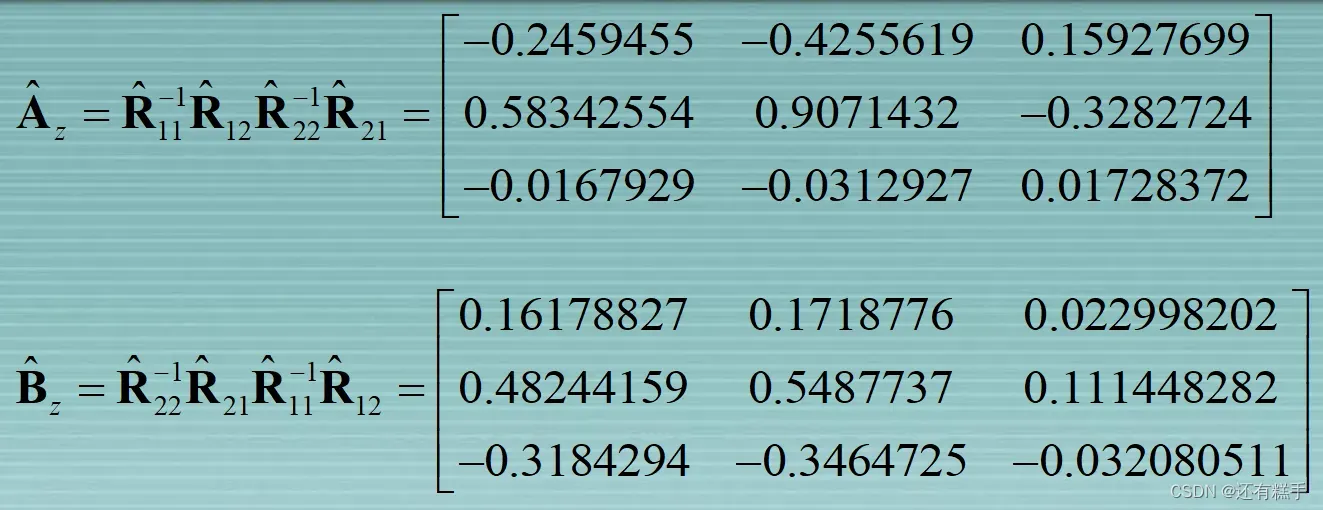
这里A和B的特征值是相同的


则可得

每一个a和b都是对应的特征向量,在这里也就是典型相关系数

第二对和第三对也是如此。
③假设检验
对于每一对典型变量进行计算




④典型载荷分析
进行典型载荷分析有助于更好解释分析已提取的p对典型变量。所谓的典型载荷分析是指原始变量与典型变量之间相关性分析。



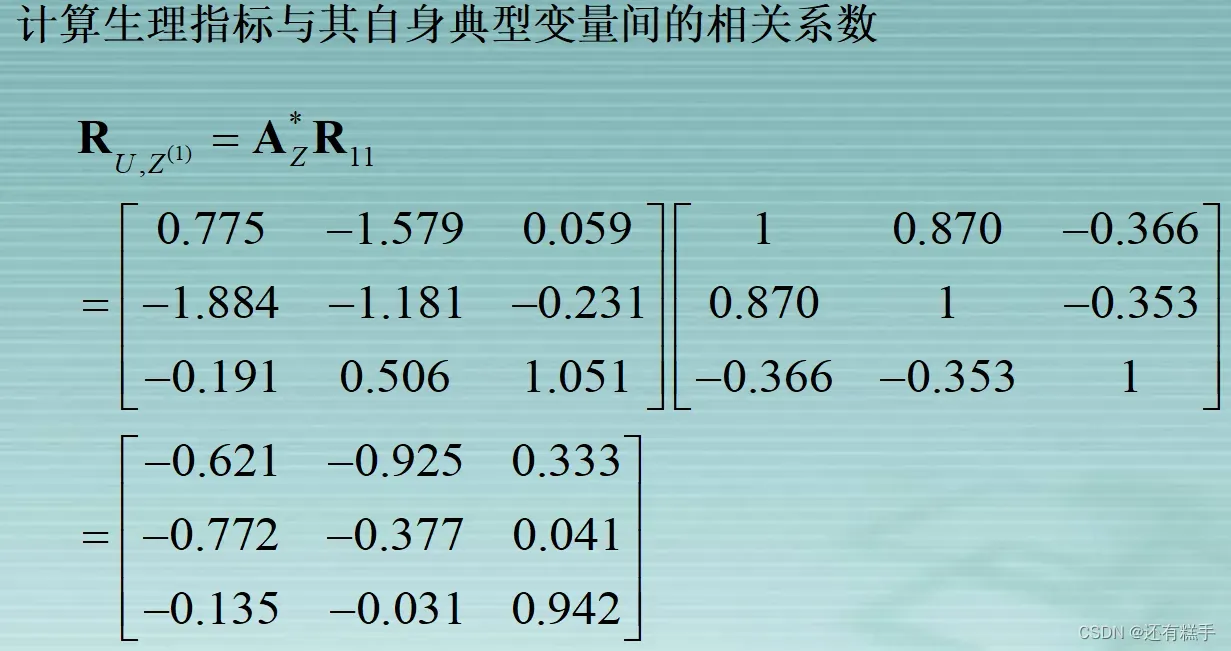

⑤典型冗余分析







5.补充
可以看见,典型相关分析过于复杂,不过可以利用SPSS软件完成对数据相关性的分析,包括pearson相关系数和spearman等级相关系数。
版权声明:本文为博主作者:还有糕手原创文章,版权归属原作者,如果侵权,请联系我们删除!
