1. AI技术聚合首页
  2. IT

探索数据结构：BF与KMP的灵活应用

心中带点小风骚 • • IT • 阅读 26

✨✨ 欢迎大家来到贝蒂大讲堂✨✨

🎈🎈养成好习惯，先赞后看哦~🎈🎈

所属专栏：数据结构与算法
贝蒂的主页：Betty’s blog

1. 什么是字符串匹配算法

字符串匹配是计算机科学中的一个基础概念，广泛应用于文本处理、数据挖掘、搜索引擎等领域。它的目的是在一个给定的文本串中寻找指定子串是否存在。由此，衍生了一系列的算法(如BF，BM，RK，KMP)就是我们的字符串匹配算法。

下面我们将选取两个最经典的BF与KMP算法为大家演示。

2. BF算法

2.1. 算法原理

BF算法，即暴力(Brute Force)算法，是普通的模式匹配算法，BF算法的思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配，若相等，则继续比较S的第二个字符和 T的第二个字符；若不相等，则比较S的第二个字符和T的第一个字符，依次比较下去，直到得出最后的匹配结果。BF算法是一种蛮力算法。

​ ——-以上摘自百度百科

2.2. 图例演示

上面的文字可能过于抽象，我们可以通过图示来为大家演示一下算法流程。

假设我们有两个字符串，分别记为s1与s2。其中s1是主串，s2为子串，即从s1中匹配s2。

img

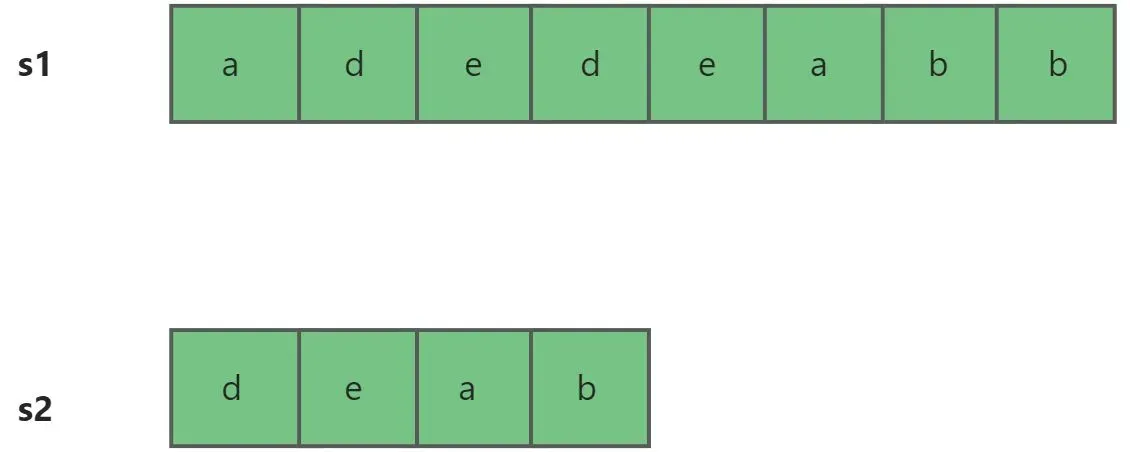
  1. 第一步都从字符串的起始位置开始匹配。

img

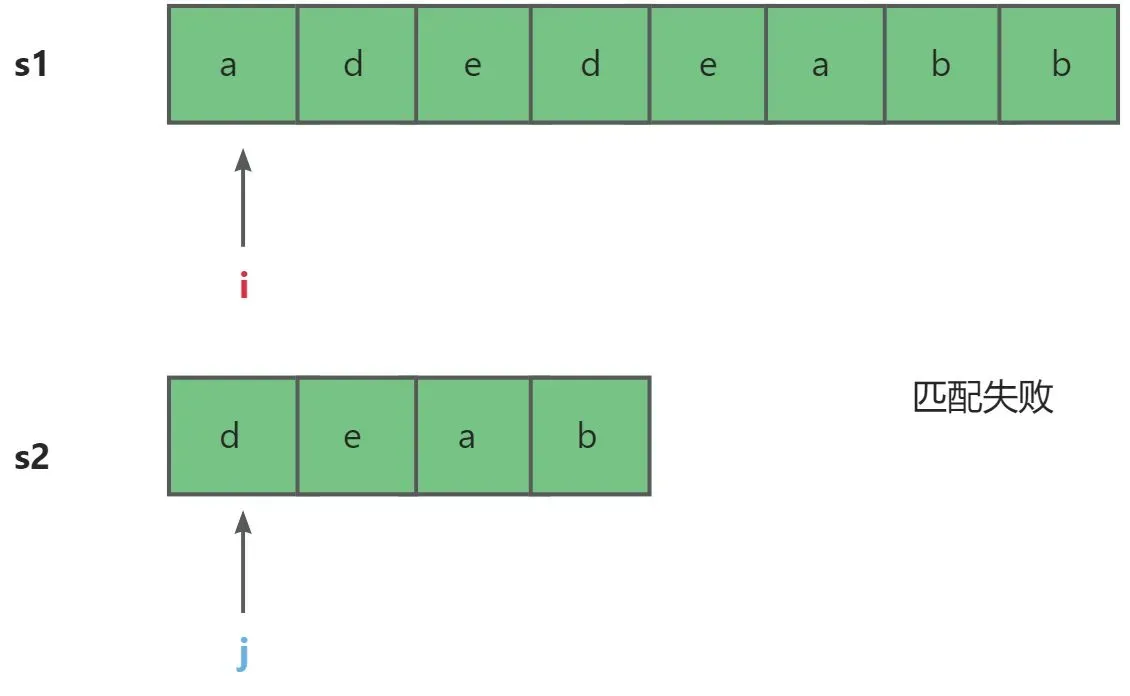
  1. 相等则继续匹配，否则从s1的下一个位置重新开始匹配。然后一直重复上述过程。

img

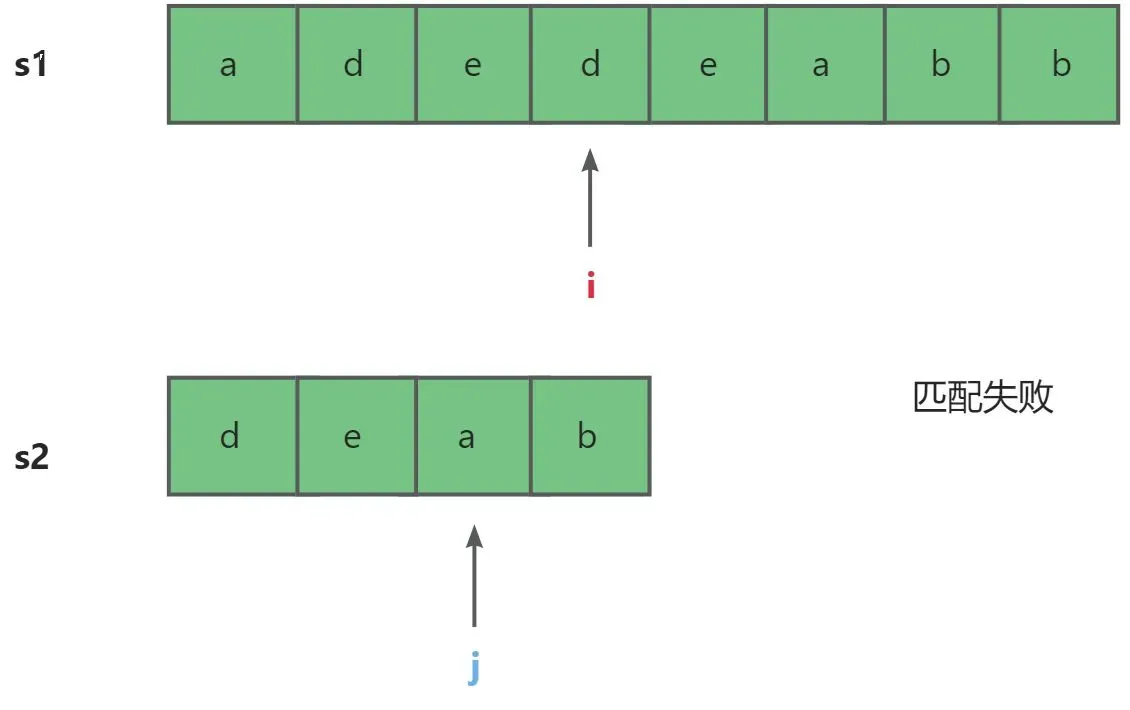
  • 这里我们就需要思考一个问题，匹配失败如何返回s1的下一个位置重新匹配。其实特别简单，我们要知道j下标如果从零开始就代表成功匹配的个数。我们只需让i下标减去j下标就会回到原来的起始位置，这是再加1就是我们下一次匹配的开始位置。

img

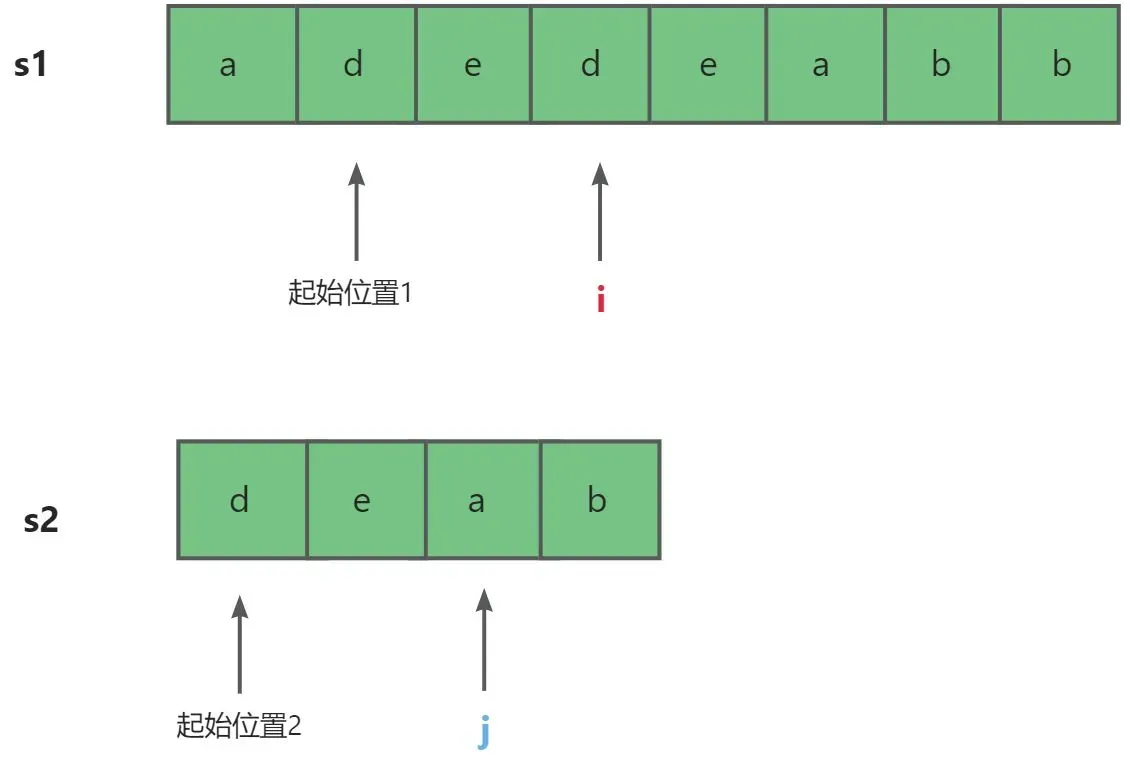
  • 起始位置1与i下标之间的元素个数就是j下标与起始位置2之间的个数。所以i-起始位置1=j-起始位置2=>起始位置1=i-j。
  1. 最后当j移动至末尾证明匹配成功，返回s1成功的匹配成功的起始下标。当i移动到末尾时，匹配失败返回-1。

2.3. 代码实现

下面是具体的代码实现，其中串是以顺序串的形式实现。

int BF(Sstring* s1, Sstring* s2)
{
	assert(s1 && s2);
	int len1 = StrLength(s1);
	int len2 = StrLength(s2);
    if (len1 == 0 || len2 == 0)
	{
		return -1;
	}
	int i = 0;//主串下标
	int j = 0;//子串下标
	while (i < len1 && j < len2)
	{
		if (s1->data[i] == s2->data[j])//匹配成功
		{
			i++;
			j++;
		}
		else
		{
			j = 0;
			i = i - j + 1;
		}
	}
	if (j >= len2)//匹配失败
	{
		return i - j;
	}
	return -1;
}

2.4. 复杂度分析

我们用M表示主串的长度，N表示子串的长度。

  • **时间复杂度：**BF算法最理想的时间复杂度是O(N)，即在主串的最开始位置就找到。最坏的时间复杂度为O(NM)，即找不到或者在最后才找到。这里我们以最坏的情况作为参考，所以时间复杂度为O(NM)。
  • 空间复杂度：BF算法并不需要格外的空间消耗，所以空间复杂度为O(1)。

3. KMP算法

KMP算法是三位学者(Knuth-Morris-Pratt )在 Brute-Force算法的基础上同时提出的模式匹配的改进算法。Brute- Force算法在模式串中有多个字符和主串中的若干个连续字符比较都相等,但最后一个字符比较不相等时,主串的比较位置需要回退。

3.1. 算法原理

在介绍算法原理之前，我们要先了解几个新概念。

  • 后缀：是指从串某个位置i开始到整个串末尾结束的一个特殊子串。记为s[i,s.length-1]，例如”adb”就是字符串”abcadb”的一个后缀。
  • 真后缀：除了字符串s本身之外的后缀。
  • 前缀：指从串首开始到某个位置i结束的一个特殊子串。记为s[0，i]，例如”abc”就是字符串”abcadb”的一个前缀。
  • 真前缀：除了字符串s本身之外的前缀。
  • 最长公共真前后缀：最长相等的真后缀与真前缀，例如”abcdab“的最长公共前后缀就是”ab”。

而KMP 方法算法就利用之前判断过的信息，通过一个 next 数组，保存模式串中前后最长公共子序列的长度(最长公共真前后缀)，每次回溯时，通过 next 数组找到，前面匹配过的位置，省去了大量的计算时间。

KMP算法在上述情况下,主串位置不需要回退,从而可以大大提高效率

​ ——-以上摘自百度百科

3.2. 图例演示

KMP算法一个非常重要的思想就是指向主串s1的下标i不回退，以此来解决BF算法i不断回退造成大量时间消耗的问题。

那么既然s1的下标不回退，自然是**回退模式串s2的下标j。**那么j下标该回退到哪一个位置呢？我们可以来看一下下图：

img

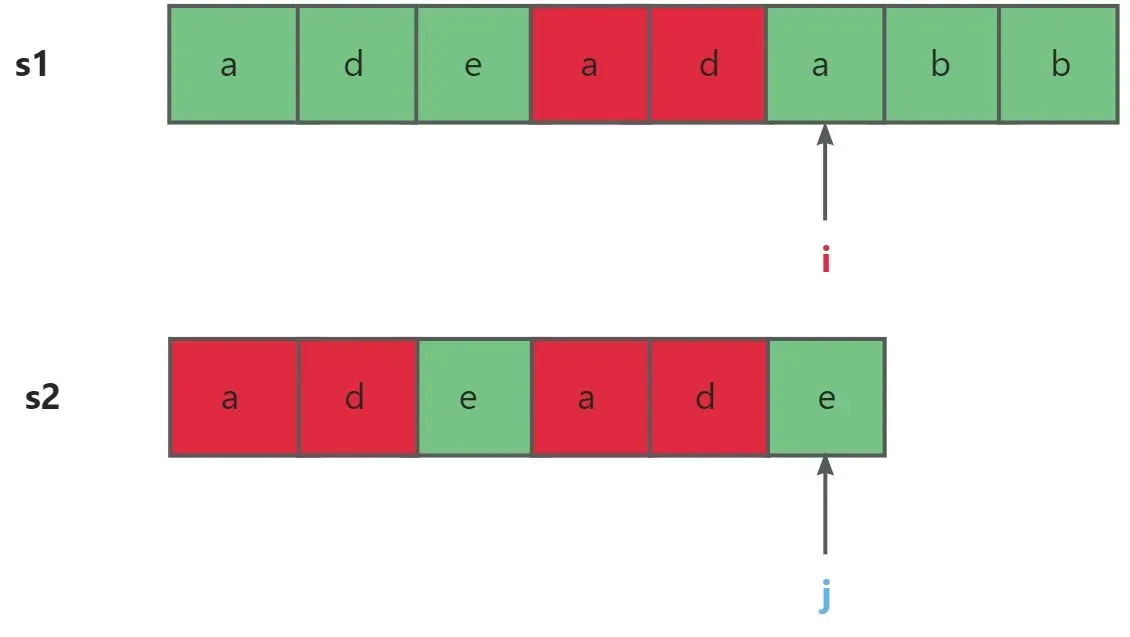
从上述观察我们不难发现，如果匹配失败，i如果不回退，j就要回退到e的下标继续匹配。其实我们想我们的模式串s2每一个位置都有可能匹配失败，那么每个位置都应该有一个与之对应的回退下标。这个我们就之存入一个数组中方便取用，这就是我们的next数组。

3.3. 求next数组

KMP算法的精髓就在于next数组，记作next[j]=k，j使我们的移动下标，k就是我们的回退下标，也是最长公共真前后缀的长度。求next数组我们分为以下几步：

  1. 首先第一步求匹配串的最长公共真前后缀(前缀以下标0开始，后缀以j-1结束)，记作s2[0,p1]=s2[p2,j-1]，其中p1-0=j-1-p2=>p2=j-1-p1。所以又可以记作s2[0,p1]=s2[j-1-p1,j-1]。

img

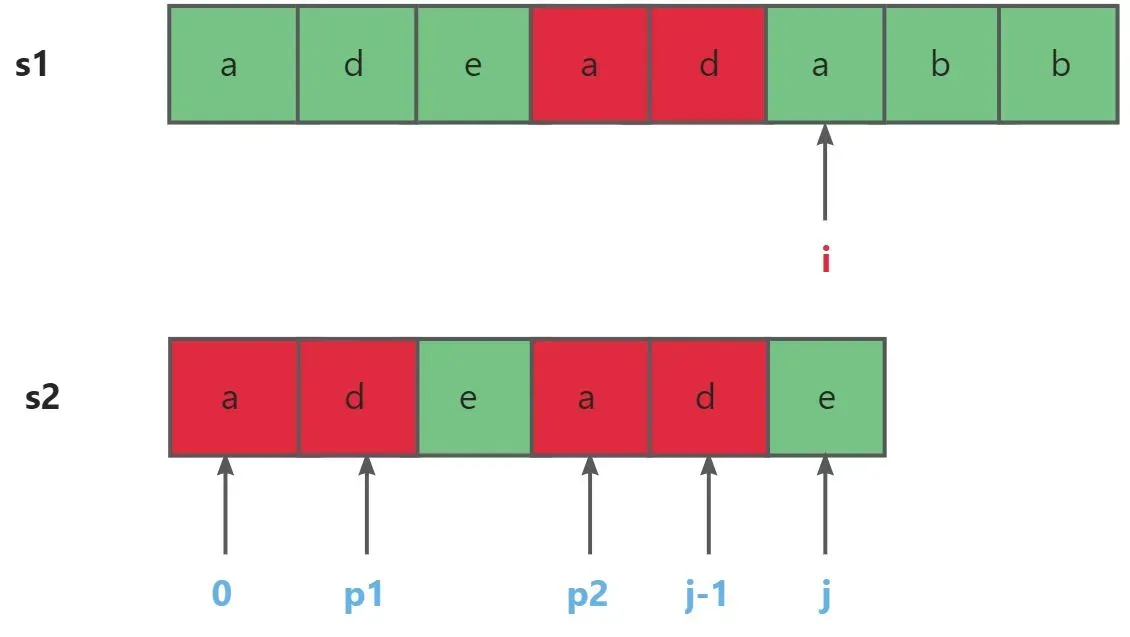
  1. 第二步求回退下标k，k的值就是匹配串前缀的下一个位置p1+1，所以k=p1+1。这只是我们通过观察得出的结论，如果每次都要重新找最长公共真前后缀，又会浪费大量时间。所以我们可以采取另一种方式：

首先我们先规定next[0]=-1，next[1]=0。并且设next[j]=k，那么问题就是求next[j+1]=？

并且我们得知道 next[j]=k<=>s2[0,k-1]=s2[j-k,j-1]+公共真前后缀最长为k ，这时我们又可以分为两种情况讨论：

  • 情况一：当s2[k]==s2[j]时，因为next[j]=k，所以s2[0,k-1]=s2[j-k,j-1]，最长公共真前后缀为k。所以s2[0,k]=s2[j-k,j]，k+1显然也是最长公共真前后缀=>next[j+1]=k+1。匹配成功将i下标与j下标往后移，继续匹配，并且k也需要递增。

img

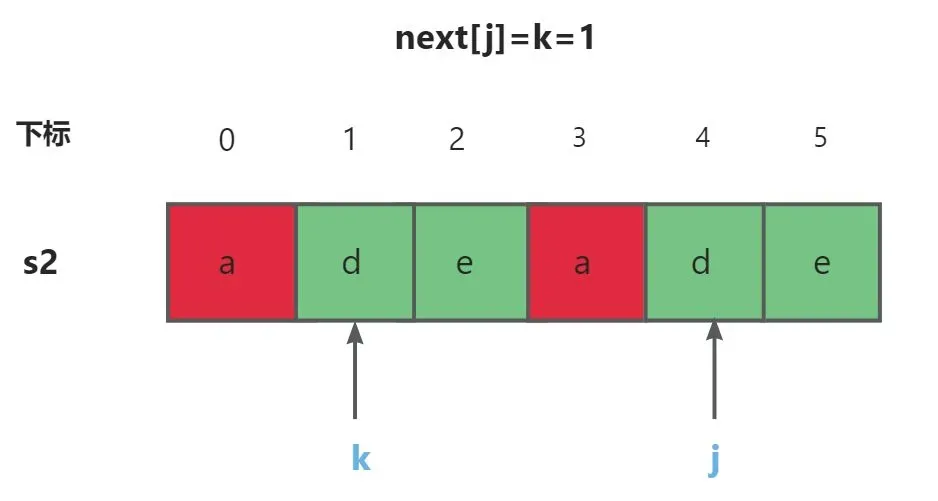
  • 情况二：当s2[k]!=s2[j]时，这时我们需要重新匹配最长公共真前后缀。这时我们不妨设k1=next[k]，因为s2[0,k-1]=s2[j-k,j-1]，所以推出**s2[0,k1-1]** =s2[k-k1,k-1]=s2[j-k,j-k+k1-1]=**s2[j-k1,j-1]****，**因为我们要求的是next[j+1]，所以这时若s2[k1] = s2[j]，则此时s2[0,k1]=s2[j-k1,j]，参考情况一next[j]=k1+1，否则设k2=next[k1]重复上述过程，若存在kn=-1，循环结束让next[j]=0即kn+1。
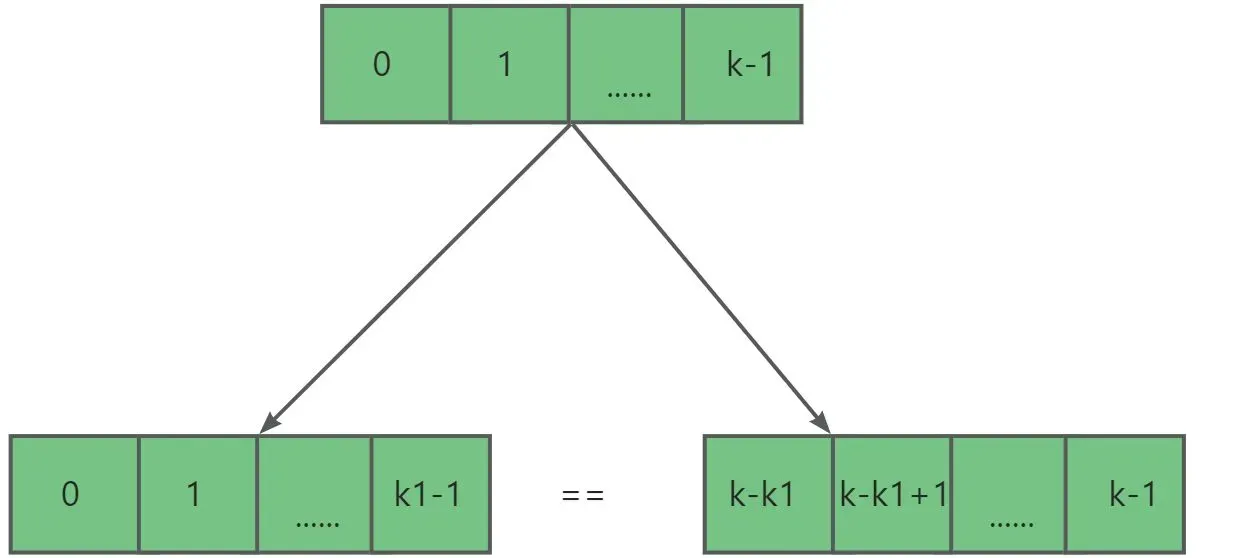
  1. 问题一：如何推出s2[0,k1-1]=s2[k-k1,k-1]=s2[j-k,j-k+k1-1]

首先由条件得s2[0,k-1]=s2[j-k,j-1]，并且s2[0,k-1]，s2[j-k,j-1]都能继续分出最长公共真前后缀(不能划分时，kn=-1）。

img

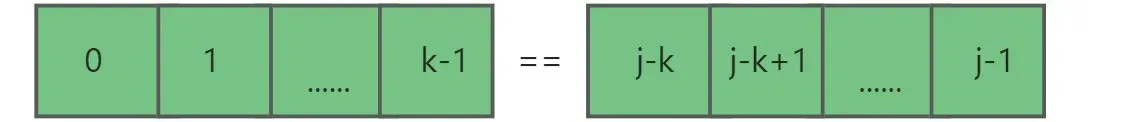
然后因为k1=next[k]，我们可以将s2[0,k-1]分解成两个相同的真前后缀s2[0,k1-1**]**=s2[k-k1,k-1]。s2[j-k,j-1]同理也可以分解出两个相同真前后缀s2[j-k,j-k+k1-1]=s2[j-k1,j-1]。又因为两个原串相等，所以这这四个子串相等，s2[0,k1-1]=s2[k-k1,k-1]=s2[j-k,j-k+k1-1]=s2[j-k1,j-1]。

img

  1. 问题二：如何保证当s2[0,k1]=s2[j-k1,j]时是最长公共真前后缀，我们可以先假设s2[0,k1]=s2[j-k1,j]不是最长。即存在当s2[0,k1+1]=s2[j-k1-1,j]时最长公共真前后缀>=k1+2。由问题一可以推出s2[0,k1+1]=s2[k-k1-1,k]=>s2[0,k1]=s2[k-k1-1,k-1]，又因为s2[0,k1+1]=s2[j-k1-1,j]时最长公共真前后缀>=k1+2，所以当s2[0,k1]=s2[k-k1-1,k-1]时最长公共真前后缀至少为k1+1即next[k]>=k1+1与题意next[k]=k1相矛盾，所以当s2[0,k1]=s2[j-k1,j]时是最长公共真前后缀。

  2. 问题三：为什么这两步求出的回退下标就能让主串的下标不回退呢？

我们可以看看这幅图

img

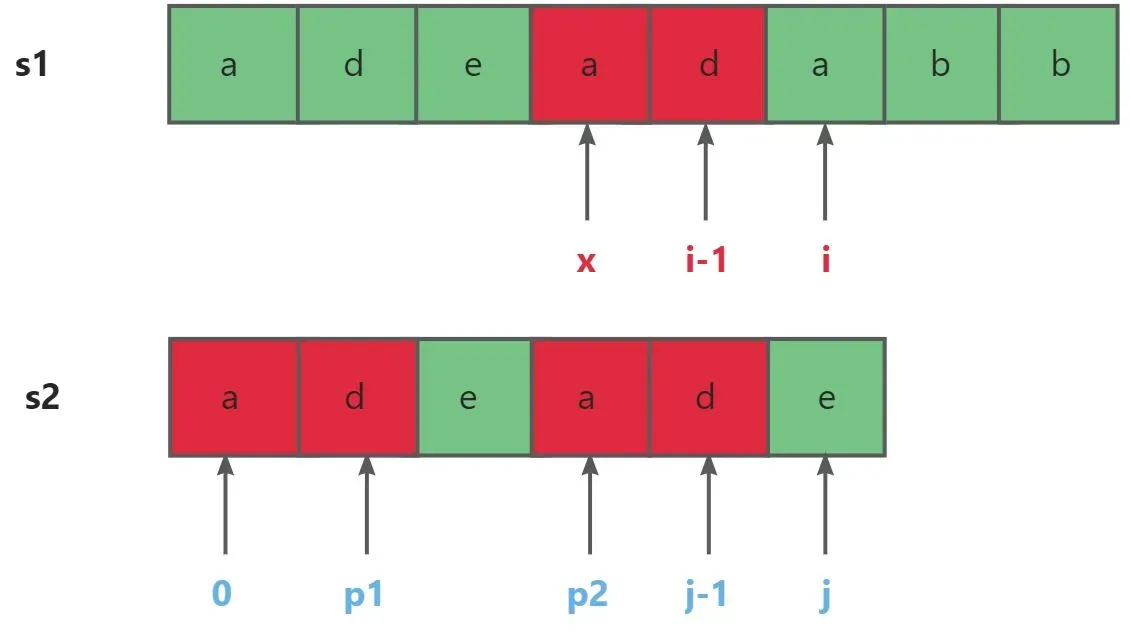
我们继续以上面的图举例，当主串s1与匹配串s2出现不匹配的情况时前面的字符是匹配成功的。也就是说s1[0,i-1]=s2[0,j-1]。s2[0,p1]与s2[j-1-p1,j-1]又是最长公共真前后缀。

所以就可以推出一定存在x使得s1[x,i-1]=s2[0,p1]=s2[j-1-p1,j-1]**。所以说x~i-1就是能在模式串s2中从起始位置匹配的最长长度。**自然主串的i下标就不用回退了。

3.4. 算法优化

虽然上述的算法在绝大数情况下运算速率都比较优秀，但是也许考虑一些特殊情景，比如说下面这种情况。

img

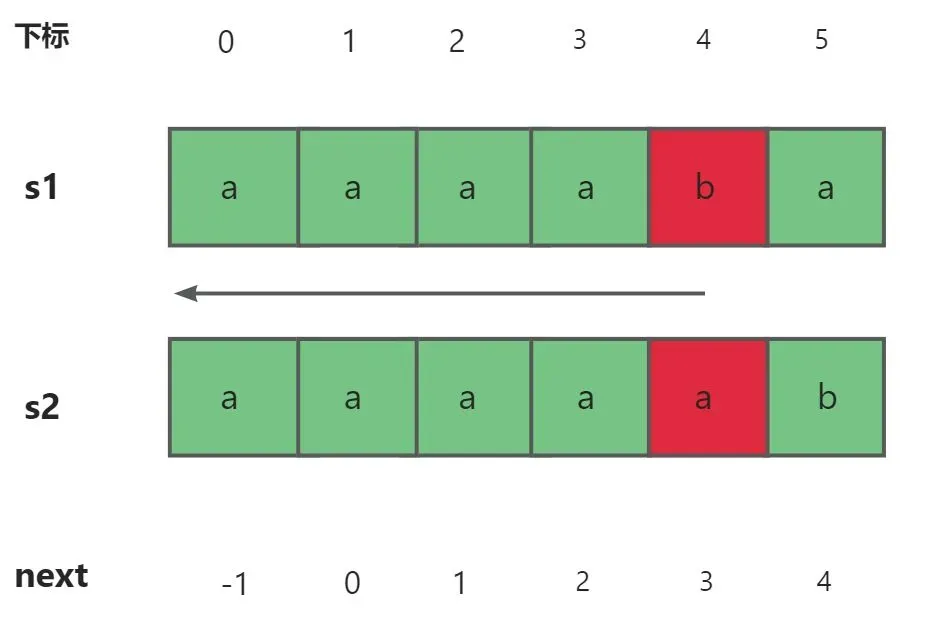
如果出现上述情况，模式串s2的下标会依次从4->3->2->1->0。这就导致一个问题，如果模式串过长出现这种情况，也会造成大量的时间销毁。

通过上述列子，我们不难发现出现这种情况是因为当k=next[j]时，s2[k]=s[j]，又因为s[j]!=s[i]，自然s[k]!=s[i]。所以就会出现一直回退的现象，因此引出了我们的优化nextval数组。

nextval数组是在原来next数组的基础上增加一个判断条件，即若s2[k]=s[j]就让nextval[j]更新成nextval[k]实现一步到位的结果，从而节约效率。

3.5. 代码实现

代码仍是以数组串的形式实现。

3.5.1. 未优化之前

  1. 创建一个next数组，按照next的实现方式填充。

    • 首先开辟s2.length的空间，并将next[0]=1。
    • 然后循环遍历更新，如果k==-1或者str2[i - 1] == str2[k]，则nextval[i] = k + 1，并且让i++，k++。否则将k=next[k]。

  2. 然后分别用两个下标i，j指向主串与匹配串，开始遍历。

  3. 如果匹配相同，或者j=-1将让两个下标右移匹配下一个字符。匹配失败将让j下标回到next数组对应位置。

  4. 重复上述步骤，成功则返回主串匹配成功开始的下标。反之找不到，则返回-1.

int* GetNext(Sstring* s2)
{
	char* str2 = s2->data;
	int len = StrLength(s2);
	int* next = (int*)malloc(sizeof(int) * len);//开辟空间
	if (next == NULL)
	{
		perror("malloc fail:");
		return NULL;
	}
	next[0] = -1;
	int i = 1;//当前下标
	int k = -1;//前一项的k
	while(i<len)
	{
		//kn=-1或者情况一
		if (k==-1||str2[i - 1] == str2[k])
		{
			next[i] = k + 1;
			i++;
			k++;
		}
		else
		{
            //情况二
			k = next[k];
		}
	}
	return next;
}
int KMP(Sstring* s1, Sstring* s2, int pos)
{
    //首先判断边界条件
	assert(s1 && s2);
	int len1 = StrLength(s1);
	int len2 = StrLength(s2);
	if (len1 == 0 || len2 == 0)
	{
		return -1;
	}
	if (pos < 0 && pos >= len1)
	{
		return -1;
	}
	int* next = GetNext(s2);
	int i = pos;
	int j = 0;
	while (i < len1 && j < len2)
	{
		if (j == -1 || s1->data[i] == s2->data[j])
		{
			i++;
			j++;
		}
		else
		{
			j = next[j];//更新至next数组
		}
	}
	if (j >= len2)//参考BF实现逻辑
	{
		return i - j;
	}
	free(next);//释放内存
	return -1;
}
3.5.2. 优化之后

相较于优化之前，优化后更新nextval时需判断此时的s2[j]是否等于s2[k+1]，等于nextval[i] = nextval[k+1]，否则nextval[i] = k + 1。

int* GetNext(Sstring* s2)
{
	char* str2 = s2->data;
	int len = StrLength(s2);
	int* nextval = (int*)malloc(sizeof(int) * len);//开辟空间
	if (nextval == NULL)
	{
		perror("malloc fail:");
		return NULL;
	}
	nextval [0] = -1;
	int i = 1;//当前下标
	int k = -1;//前一项的k
	while(i<len)
	{
		if (k==-1||str2[i - 1] == str2[k])
		{
			if (str2[k+1] == str2[i])//相等
			{
				nextval[i] = nextval[k+1];//更新
			}
			else
			{
				nextval[i] = k + 1;
			}
			k++;
			i++;
		}
		else
		{
			k = nextval[k];
		}
	}
	return nextval;
}
int KMP(Sstring* s1, Sstring* s2, int pos)
{
	assert(s1 && s2);
	int len1 = StrLength(s1);
	int len2 = StrLength(s2);
	if (len1 == 0 || len2 == 0)
	{
		return -1;
	}
	if (pos < 0 && pos >= len1)
	{
		return -1;
	}
	int* nextval = GetNext(s2);
	int i = pos;
	int j = 0;
	while (i < len1 && j < len2)
	{
		if (j == -1 || s1->data[i] == s2->data[j])
		{
			i++;
			j++;
		}
		else
		{
			j = nextval[j];//更新至next数组
		}
	}
	if (j >= len2)
	{
		return i - j;
	}
	free(nextval);//释放内存
	return -1;
}

3.6. 复杂度分析

我们用M表示主串的长度，N表示模式串的长度。

  • 时间复杂度：主串并不回退，时间复杂度为O(M)，模式串时间复杂度也可以近似看做O(N)，即使在最坏情况下，KMP 算法的时间复杂度为 O(mn)，但这种情况很少发生，通常情况下，KMP 算法的时间复杂度是线性的，可以在很短的时间内完成字符串匹配。
  • 空间复杂度：开辟了一个nextval数组，空间复杂度为O(N)。

版权声明：本文为博主作者：Betty’s Sweet原创文章，版权归属原作者，如果侵权，请联系我们删除！

原文链接：https://blog.csdn.net/Bettysweetyaaa/article/details/137858475

共计人评分，平均分

到目前为止还没有投票！成为第一位评论此文章。

赞 (0)
心中带点小风骚的头像心中带点小风骚普通用户
0
上一篇 2024年4月22日
下一篇 2024年4月22日

相关推荐