提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

前言

本文采用SVM进行手写数字识别；

主要使用MATLAB进行代码编写，处理MNIST数据集利用PYTHON；

数据集为MNIST手写数字，训练集大致有60000张图片，测试集有20000张图片；

文章目录

SVM原理简介
实验步骤
实验分析
完整代码

SVM原理简介

支持向量机大致包含以下三个方面内容：1、线性可分支持向量机；2、线性支持向量机；3、线性不可分支持向量机；其中线性可分支持向量机是其余两个支持向量机的基础，其针对的是线性可分的数据集；线性支持向量机则是针对近似线性可分的数据集；非线性支持向量机则是针对非线性可分的数据集。

支持向量机的基本思想就是求解能够正确划分训练数据集并且几何间隔最大的分离超平面；所谓几何间隔用于表示分类正确度以及确信度的一个概念。

线性可分支持向量机

以下先进行线性可分支持向量机介绍：

假设给定特征空间上线性可分的训练数据集

$T = \left\{ {\left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right),...,\left( {{x_N},{y_N}} \right)} \right\}$

其中 ${x_i} \in \aleph = {^n}$ ， ${y_i} \in \gamma = \left\{ { + 1, - 1} \right\}$ ， $i = 1,2,...,N$

1.1、函数间隔与几何间隔定义

下面给出函数间隔与几何间隔的定义：

给定训练数据集 $T$ 和超平面 $\omega {x_{}} + b = 0$

${\hat \nu _i} = {y_i}\left( {\omega {x_i} + b} \right)$

函数间隔能够表示样本点分类正确性与离超平面远近；

定义在训练集 $T$ 中，所有样本点函数间隔最小值：

$\hat \nu = \mathop {\min }\limits_{i = 1,...,N} {\hat \nu _i}$

由于 ${\hat \nu _i}$ 会随着 $\omega$ 的变化而进行改变，因此我们定义几何间隔来更好地表示样本点被分类的正确性与确信度：

${\nu _i} = \frac{{{{\hat \nu }_i}}}{{\left\| \omega \right\|}}$

同样的可以定义训练集 $T$ 中，所有样本点几何间隔最小值：

$\nu = \mathop {\min }\limits_{i = 1,...,N} {\nu _i}$

支持向量机的任务就是寻找一个超平面能够正确划分数据集并且几何间隔最大，也就是最小间隔最大化；上述问题可以描述为：

$\begin{array}{l} \mathop {\max }\limits_{\omega ,b} \nu \\ s.t.{\rm{ }}{y_i}(\frac{\omega }{{\left\| \omega \right\|}}{x_i} + \frac{b}{{\left\| \omega \right\|}}) \ge \nu ,{\rm{ }}i = 1,2,...,N \end{array}$

将其改写为函数间隔形式：

$\begin{array}{l} \mathop {\max }\limits_{\omega ,b} \frac{{\hat \nu }}{{\left\| \omega \right\|}}\\ s.t.{\rm{ }}{y_i}(\omega {x_i} + b) \ge \hat \nu ,{\rm{ }}i = 1,2,...,N \end{array}$

由于几何间隔只与超平面方向有关，与其大小无关，因此可以通过变化大小，将固定为1，因此上述可以转化为：

$\begin{array}{l} \mathop {\max }\limits_{\omega ,b} \frac{1}{{\left\| \omega \right\|}}\\ s.t.{\rm{ }}{y_i}(\omega {x_i} + b) \ge 1,{\rm{ }}i = 1,2,...,N \end{array}$

进而转化为以下等价形式：

$\begin{array}{l} \mathop {\max }\limits_{\omega ,b} \frac{1}{2}{\left\| \omega \right\|^2}\\ s.t.{\rm{ }}{y_i}(\omega {x_i} + b) \ge 1,{\rm{ }}i = 1,2,...,N \end{array}$

1.2、对偶算法

对于以上问题，主要通过利用拉格朗日对偶性，通过求解对偶问题来求得原问题的解；

先进行拉格朗日函数的构建：

$L(\omega ,b,\alpha ) = \frac{1}{2}{\left\| \omega \right\|^2} - \sum\limits_{i = 1}^N {{\alpha _i}{y_i}(\omega {x_i} + b) + \sum\limits_{i = 1}^N {{\alpha _i}} }$

原始问题为：

$\begin{array}{l} \mathop {\max }\limits_{\omega ,b} \frac{1}{2}{\left\| \omega \right\|^2}\\ s.t.{\rm{ }}{y_i}(\omega {x_i} + b) \ge 1,{\rm{ }}i = 1,2,...,N \end{array}$

该问题等价于以下问题：

$\mathop {\min }\limits_{\omega ,b} \mathop {\max }\limits_{\alpha \ge 0} L(\omega ,b,\alpha )$

根据拉格朗日对偶性，原问题的对偶问题为：

$\mathop {\max }\limits_{\alpha \ge 0} \mathop {\min }\limits_{\omega ,b} L(\omega ,b,\alpha )$

通过对求导数，并令其为0：

${\nabla _{\omega ,b}}L(\omega ,b,\alpha ) = 0$

求解该对偶问题，得到以下与之等价的最优化问题：

$\begin{array}{l} \mathop {\min }\limits_\alpha \frac{1}{2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{\alpha _i}{\alpha _j}{y_i}{y_j}({x_i}{x_j})} } - \sum\limits_{i = 1}^N {{\alpha _i}} \\ s.t.{\rm{ }}\sum\limits_{i = 1}^N {{\alpha _i}{y_i} = 0} \end{array}$

对偶问题最优解与原始问题最优解存在着一定联系，该联系表述为：

满足一定条件，原始问题最优解与对偶问题最优解满足KKT条件；

设 ${\alpha ^*}$ 是对偶问题最优解，存在下标 $j$ 使得，原始问题最优解为：

$\begin{array}{l} {\omega ^*} = \sum\limits_{i = 1}^N {\alpha _i^*{y_i}{x_i}} \\ {b^*} = {y_j} - \sum\limits_{i = 1}^N {\alpha _i^*{y_i}({x_i}{x_j})} \end{array}$

最后，运用得到的最优超平面 $({\omega ^*},{b^*})$ 通过 $f(x) = sign({\omega ^*}x + {b^*})$ 对样本点 $x$ 进行分类。

二．线性支持向量机

给定近似线性可分的训练数据集，这意味着不存在一个超平面能够将两类数据完美分开，为了解决这个问题，通过引入松弛变量，将原先约束条件变得宽松：

${y_i}(\omega {x_i} + b) \ge 1 - {\xi _i}$

对于原先问题转化为如下问题：

$\begin{array}{l} \mathop {\max }\limits_{\omega ,b} \frac{1}{2}{\left\| \omega \right\|^2} + C\sum\limits_{i = 1}^N {{\xi _i}} \\ s.t.{\rm{ }}{y_i}(\omega {x_i} + b) \ge 1 - {\xi _i},{\rm{ }}i = 1,2,...,N\\ {\rm{ }}{\xi _i} \ge 0,{\rm{ }}i = 1,2,...,N \end{array}$

同理，利用线性可分支持向量机中对偶问题转化，该问题对偶问题为：

同理，存在下标 $j$ 使得 $0 < \alpha _j^* < C$ ，计算原始问题最优解：

$\begin{array}{l} {\omega ^*} = \sum\limits_{i = 1}^N {\alpha _i^*{y_i}{x_i}} \\ {b^*} = {y_j} - \sum\limits_{i = 1}^N {\alpha _i^*{y_i}({x_i}{x_j})} \end{array}$

三、非线性可分支持向量机

给定一线性不可分数据集，我们可以利用函数映射技巧，将原始数据点映射到更高维的特征空间中，这样在更高维空间中，数据集就是线性可分或者近似线性可分的，就可以利用之前得到的结果进行计算。

3.1、核函数技巧

设 $\aleph$ 是输入特征空间， $H$ 为另外一个特征空间，如果存在一个从 $\aleph$ 到 $H$ 的一个映射 $\phi (x)$ ： $\aleph \to {\rm H}$ ， $K(x,z) = \phi (x) \bullet \phi (z)$ ，我们称 $K(x,z)$ 为核函数。

借助核函数技巧，可以不用给出具体的映射 $\phi (x)$ ，只需计算 $K(x,z)$ 即可；

3.2、核函数技巧在支持向量机中应用

利用核函数技巧将原先的问题中所有涉及内积 $({x_i}{x_j})$ 替换为 $K({x_i},{x_j})$ ，转换为以下问题：

$\begin{array}{l} \mathop {\min }\limits_\alpha \frac{1}{2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{\alpha _i}{\alpha _j}{y_i}{y_j}K({x_i},{x_j})} } - \sum\limits_{i = 1}^N {{\alpha _i}} \\ s.t.{\rm{ }}\sum\limits_{i = 1}^N {{\alpha _i}{y_i} = 0} \end{array}$

原先的决策函数式改写为 $f(x) = sign(\sum\limits_{i = 1}^N {\alpha _i^*{y_i}K({x_i},{x_j})} + {b^*})$

SMO算法

通过先前讨论我们清楚，凸优化问题可以转化为其对偶形式问题的最优化：

该问题是一个凸二次规划问题，SMO算法是一种启发式算法，基本思路是如果所有变量满足KKT条件，那么该问题的最优解也就得到了；选择两个变量，固定其他变量，更新这两个变量的值进行优化，直到没有变量违反条件为止。

4.1、变量选择

我们通过以下方式进行样本点 $({x_i},{y_i})$ 是否满足KKT条件的检验：

$\begin{array}{l} {\alpha _i} = 0 \Leftrightarrow {y_i}g({x_i}) \ge 1\\ 0 < {\alpha _i} < C \Leftrightarrow {y_i}g({x_i}) = 1\\ {\alpha _i} = C \Leftrightarrow {y_i}g({x_i}) \le 1 \end{array}$

其中 $g(x) = \sum\limits_{i = 1}^N {\alpha _i^{}{y_i}K({x_i},x)} + {b^{}}$

外层循环遍历数据集寻找不满足KKT条件的数据点，作为第一个变量的选择；

为了加速运算，我们希望更新幅度越大越好，因此我们通过寻找 $\left| {{E_1} - {E_2}} \right|$ 最大的作为第二个变量的选择。

4.2、变量更新

现在已经选择两个变量 ${\alpha _1},{\alpha _2}$ ，固定其余变量，原问题可以转化为关于 ${\alpha _1},{\alpha _2}$ 的最优化问题，考虑到约束条件 ${\alpha _1}{y_1} + {\alpha _2}{y_2} = - \sum\limits_{i = 3}^N {{y_i}{\alpha _i}}$ ，因此 ${\alpha _1}$ 与 ${\alpha _2}$ 是在一条直线上的，将 ${\alpha _1}$ 转化为 ${\alpha _2}$ 的变量进行运算；

$\alpha _2^{new}$ 需要满足一定的条件：

$L \le \alpha _2^{new} \le H$

其中 $L$ 和 $H$ 分别为对角线两端的端点的解；

若 ${y_1} \ne {y_2}$ ， $L = \max (0,\alpha _2^{old} - \alpha _1^{olld})$ ， $H = \min (C,C + \alpha _2^{old} - \alpha _1^{old})$

若 ${y_1} = {y_2}$ ， $L = \max (0,\alpha _2^{old} + \alpha _1^{olld} - C)$ ， $H = \min (C,\alpha _2^{old} + \alpha _1^{old})$

记 ${E_i}$ 为 $g(x)$ 对 ${x_i}$ 的预测值与真实输出 ${y_i}$ 之差；

${E_i} = g({x_i}) - {y_i},{\rm{ }}i = 1,2$

为经过裁剪的 $\alpha _2^{unc} = \alpha _2^{old} + \frac{{{y_2}({E_1} - {E_2})}}{\eta }$ ，

其中 $\eta = K({x_1},{x_1}) + K({x_2},{x_2}) - 2K({x_1},{x_2}) = {\left\| {\phi ({x_1}) - \phi ({x_2})} \right\|^2}$

经过裁剪得到解为：

$\alpha _2^{new} = \left\{ {\begin{array}{*{20}{c}} {H,{\rm{ }}\alpha _2^{unc} > H}\\ {\alpha _2^{unc},{\rm{ }}L \le \alpha _2^{unc} \le H}\\ {L,{\rm{ }}\alpha _2^{unc} < L} \end{array}} \right.$

计算的到 $\alpha _1^{new} = \alpha _1^{old} + {y_1}{y_2}(\alpha _2^{old} - \alpha _2^{new})$

4.3、SMO算法概述

（1）取初始值 ${\alpha ^{(0)}} = 0$ ；

（2）选取优化变量 $\alpha _1^{(k)},\alpha _2^{(k)}$ ，进行更新为 $\alpha _1^{(k + 1)},\alpha _2^{(k + 1)}$ ；

（3）在精度范围内，如果每个都满足KKT条件，则停机；

（4）否则 $k = k + 1$ 转（2）

（5） $\alpha = {\alpha ^{(k + 1)}}$

实验步骤

一、算法设计

网上下载MNIST的手写数字数据集，并将其解析为CSV格式文件，其中每一行为一个样本，第一列为标签值，剩余列为特征值；
划分训练集以及测试集，训练集有60000张图片，测试集有20000张图片；
在训练集中，对于第类样本，将其标签值设为1，将其余别的类别样本设为-1，利用SMO算法进行训练，训练得到该类的SVM模型 $MODEL(i)$ ，模型参数包含： $MODEL(i).\ker nelFunction$ ：所使用的核函数形式、 $MODEL(i).alphas$ ： $\alpha$ 的值、 $MODEL(i).b$ ： $b$ 的值、 $MODEL(i).\omega$ ： $\omega$ 的值；
对于每一个样本 ${x_j}$ ，利用 $svm\Pr ediction(MODEL,x)$ 函数，输出样本 ${x_j}$ 在 $MODEL(i)$ 上得分，得分最高的类别为 ${x_j}$ 样本被分到的类别，即 $kind({x_j}) = \mathop {\arg }\limits_{} \mathop {\max }\limits_{i = 1,2,...} \{ svm\Pr ediction(MODEL(i),{x_j})\}$ ；
分别输出训练集正确率 $trainTrue$ 与测试集正确率 $testTrue$ ；
人为调整参数使得 $trainTrue$ 和 $testTrue$ 取得好的效果；

二、程序结构：

2.1、解析文件：

由于从网上下载下来的文件格式为idx3-ubyte、idx1-ubyte格式，因此先要进行对这两个文件进行解析，得到csv格式文件，为训练集与测试集，分别为mnist_train.csv、mnist_test.csv，其中每一行表示一个样本的特征与标签，第一列是标签，剩余列为特征；此处代码为PYTHON代码；

1.#将IDX数据转化为CSV数据
2.#每一行为一张图片， 第一列为标签值， 往后为图片信息
3.def convert(imgf, labelf, outf, n):
4.    f = open(imgf, "rb")
5.    o = open(outf, "w")
6.    l = open(labelf, "rb")
7.    f.read(16)
8.    l.read(8)
9.    images = []
10.    for i in range(n):
11.        image = [ord(l.read(1))]
12.        for j in range(28 * 28):
13.            image.append(ord(f.read(1)))
14.        images.append(image)
15.    for image in images:
16.        o.write(",".join(str(pix) for pix in image) + "\n")
17.    f.close()
18.    o.close()
19.    l.close()
20.
21.
22.convert("C:/Users/Administrator/Desktop/模式识别实验/MINIST/train-images.idx3-ubyte", "C:/Users/Administrator/Desktop/模式识别实验/MINIST/train-labels.idx1-ubyte",
23.        "C:/Users/Administrator/Desktop/模式识别实验/MINIST/mnist_train.csv", 60000)
24.convert("C:/Users/Administrator/Desktop/模式识别实验/MINIST/t10k-images.idx3-ubyte", "C:/Users/Administrator/Desktop/模式识别实验/MINIST/t10k-labels.idx1-ubyte",
25.        "C:/Users/Administrator/Desktop/模式识别实验/MINIST/mnist_test.csv", 10000)
26.
27.print("Convert Finished!")

2.2、SMO算法实现

按照SMO算法进行代码编写，

输入：训练集样本特征集X、训练集样本标签集Y、惩罚系数C、采用的核函数形式kernelFunction、最大精度范围tol、最大迭代次数max_passes；

输出：训练好的模型MODEL；此处代码为MATLAB代码；

1.function [model] = smo_quick2(X, Y, C, kernelFunction, tol, max_passes)
2.%smo_quick:加速版smo算法
3.%X:样本特征集，每一行代表一个样本
4.%Y：二分类标签集，正类为1，负类为0
5.%C：惩罚系数
6.%kernelFunction：所选核函数
7.%tol：判断相等的最大容忍值
8.%max_passes：没有alphas改变的最大迭代数
9.
10.%缺省处理方式
11.if ~exist('tol', 'var') || isempty(tol)
12.    tol = 1e-3;
13.end
14.if ~exist('max_passes', 'var') || isempty(max_passes)
15.    max_passes = 5;
16.end
17.
18.% 一些关于数据集的参数
19.m = size(X, 1);
20.n = size(X, 2);
21.
22.
23.Y(Y==0) = -1;
24.
25.% smo算法需要用的变量
26.alphas = zeros(m, 1);
27.b = 0;
28.E = zeros(m, 1);
29.passes = 0;
30.eta = 0;
31.L = 0;
32.H = 0;
33.
34.%根据所选核函数，计算Kernel矩阵
35.fprintf('******Begin to calculate Kernel mat******\n');
36.if strcmp(func2str(kernelFunction), 'linearKernel')
37.    %线性核
38.    K = X*X';
39.elseif strfind(func2str(kernelFunction), 'gaussianKernel')
40.   %RBF核
41.    X2 = sum(X.^2, 2);
42.    K = bsxfun(@plus, X2, bsxfun(@plus, X2', - 2 * (X * X')));
43.    K = kernelFunction(1, 0) .^ K;
44.else
45.    %高斯核
46.    K = zeros(m);
47.    for i = 1:m
48.        for j = i:m
49.             K(i,j) = kernelFunction(X(i,:)', X(j,:)');
50.             K(j,i) = K(i,j); %the matrix is symmetric
51.        end
52.    end
53.end
54.fprintf('******End of Kernel mat******\n');
55.% Train
56.fprintf('******Training******\n');
57.while passes < max_passes
58.    fprintf('******running now******\n');
59.    num_changed_alphas = 0;
60.    for i = 1:m
61.        E(i) = b + sum (alphas.*Y.*K(:,i)) - Y(i);
62.        %选择不满足KKT条件的alpha
63.        if ((Y(i)*E(i) < -tol && alphas(i) < C) || (Y(i)*E(i) > tol && alphas(i) > 0))
64.            %选择Ei-Ej绝对值最大的j
65.            non_zero_index = find(E ~= 0);
66.            num_E_nozero = length(non_zero_index);
67.            j = -1; max_E = 0;
68.            if num_E_nozero > 1
69.                for k = (non_zero_index)'
70.                    if k == i
71.                        continue;
72.                    end
73.                    Ek = b + sum (alphas.*Y.*K(:,k)) - Y(k);
74.                    deltaE = abs(Ek-E(i));
75.                    if deltaE >= max_E
76.                        max_E = deltaE;
77.                        j = k;
78.                    end
79.                end
80.            else
81.                j = ceil(m * rand());
82.                while j == i  
83.                    j = ceil(m * rand());
84.                end
85.            end                       
86.            E(j) = b + sum (alphas.*Y.*K(:,j)) - Y(j);            
87.            % Save old alphas
88.            alpha_i_old = alphas(i);
89.            alpha_j_old = alphas(j);            
90.            % Compute L and H by (10) or (11). 
91.            if (Y(i) == Y(j))
92.                L = max(0, alphas(j) + alphas(i) - C);
93.                H = min(C, alphas(j) + alphas(i));
94.            else
95.                L = max(0, alphas(j) - alphas(i));
96.                H = min(C, C + alphas(j) - alphas(i));
97.            end         
98.            if (L == H)
99.                % continue to next i. 
100.                %fprintf('******L=H******\n');
101.                continue;
102.            end
103.            % Compute eta by (14).
104.            eta = 2 * K(i,j) - K(i,i) - K(j,j);
105.            if (eta >= 0)
106.                % continue to next i. 
107.                fprintf('******eta>=0******\n');
108.                continue;
109.            end            
110.            % Compute and clip new value for alpha j using (12) and (15).
111.            alphas(j) = alphas(j) - (Y(j) * (E(i) - E(j))) / eta;
112.            fprintf('******New the alphas******\n');
113.            % Clip
114.            alphas(j) = min (H, alphas(j));
115.            alphas(j) = max (L, alphas(j));  
116.            E(j) = b + sum (alphas.*Y.*K(:,j)) - Y(j);
117.            % Check if change in alpha is significant
118.            if (abs(alphas(j) - alpha_j_old) < tol)
119.                fprintf('******old_alphaj=new_alphaj******\n');
120.                alphas(j) = alpha_j_old;
121.                continue;
122.            end
123.            % Determine value for alpha i using (16). 
124.            alphas(i) = alphas(i) + Y(i)*Y(j)*(alpha_j_old - alphas(j));
125.            E(i) = b + sum (alphas.*Y.*K(:,i)) - Y(i);
126.            % Compute b1 and b2 using (17) and (18) respectively. 
127.            b1 = b - E(i) ...
128.                 - Y(i) * (alphas(i) - alpha_i_old) *  K(i,j)' ...
129.                 - Y(j) * (alphas(j) - alpha_j_old) *  K(i,j)';
130.            b2 = b - E(j) ...
131.                 - Y(i) * (alphas(i) - alpha_i_old) *  K(i,j)' ...
132.                 - Y(j) * (alphas(j) - alpha_j_old) *  K(j,j)';
133.            if (0 < alphas(i) && alphas(i) < C)
134.                b = b1;
135.            elseif (0 < alphas(j) && alphas(j) < C)
136.                b = b2;
137.            else
138.                b = (b1+b2)/2;
139.            end
140.            num_changed_alphas = num_changed_alphas + 1;
141.        end        
142.    end    
143.    if (num_changed_alphas == 0)
144.        passes = passes + 1;
145.    else
146.        passes = 0;
147.    end
148.end
149.fprintf(' Done! \n\n');
150.% Save the model
151.idx = alphas > 0;
152.model.X= X(idx,:);
153.model.y= Y(idx);
154.model.kernelFunction = kernelFunction;
155.model.b= b;
156.model.alphas= alphas(idx);
157.model.w = ((alphas.*Y)'*X)';
158.End

2.3、预测样本集在模型上的得分

输入：训练得到的模型MODEL、待预测的样本集X；

输出：样本集在该MODEL上的得分p；

1.function p = svmPredict(model, X)
2.%SVMPREDICT returns a vector of predictions using a trained SVM model
3.%(svmTrain). 
4.%   pred = SVMPREDICT(model, X) returns a vector of predictions using a 
5.%   trained SVM model (svmTrain). X is a mxn matrix where there each 
6.%   example is a row. model is a svm model returned from svmTrain.
7.%   predictions pred is a m x 1 column of predictions of {0, 1} values.
8.%
9.
10.% Check if we are getting a column vector, if so, then assume that we only
11.% need to do prediction for a single example
12.if (size(X, 2) == 1)
13.    % Examples should be in rows
14.    X = X';
15.end
16.
17.% Dataset 
18.m = size(X, 1);
19.p = zeros(m, 1);
20.pred = zeros(m, 1);
21.
22.if strcmp(func2str(model.kernelFunction), 'linearKernel')
23.    % We can use the weights and bias directly if working with the 
24.    % linear kernel
25.    p = X * model.w + model.b;
26.elseif strfind(func2str(model.kernelFunction), 'gaussianKernel')
27.    % Vectorized RBF Kernel
28.    % This is equivalent to computing the kernel on every pair of examples
29.    X1 = sum(X.^2, 2);
30.    X2 = sum(model.X.^2, 2)';
31.    K = bsxfun(@plus, X1, bsxfun(@plus, X2, - 2 * X * model.X'));
32.    K = model.kernelFunction(1, 0) .^ K;
33.    K = bsxfun(@times, model.y', K);
34.    K = bsxfun(@times, model.alphas', K);
35.    p = sum(K, 2);
36.else
37.    % Other Non-linear kernel
38.    for i = 1:m
39.        prediction = 0;
40.        for j = 1:size(model.X, 1)
41.            prediction = prediction + ...
42.                model.alphas(j) * model.y(j) * ...
43.                model.kernelFunction(X(i,:)', model.X(j,:)');
44.        end
45.        p(i) = prediction + model.b;
46.    end
47.end

2.4、定义高斯核函数

高斯核函数表达式：

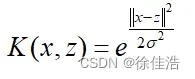
输入：向量 $x,z$

输出： $K(x,z)$

1.function sim = gaussianKernel(x1, x2, sigma)
2.%RBFKERNEL returns a radial basis function kernel between x1 and x2
3.%   sim = gaussianKernel(x1, x2) returns a gaussian kernel between x1 and x2
4.%   and returns the value in sim
5.
6.% Ensure that x1 and x2 are column vectors
7.x1 = x1(:); x2 = x2(:);
8.
9.% You need to return the following variables correctly.
10.sim = 0;
11.
12.% ====================== YOUR CODE HERE ======================
13.% Instructions: Fill in this function to return the similarity between x1
14.%               and x2 computed using a Gaussian kernel with bandwidth
15.%               sigma
16.%
17.%
18.
19.sim=(x1-x2)'*(x1-x2);
20.sim=exp(-sim/(2*sigma^2));
21.% =============================================================
22.    
23.end

2.5、随机采样函数

对数据集进行随机采样，每次生成随机随机数，采取该随机数对应的下标的样本收入集合中；

输入：数据集X，采样容量num；

输出：随机采样形成的集合sample；

1.function sample = sampling(S, num)
2.%sampling：在S中随机选择num个样本
3.fprintf('******Begin to sampling******\n');
4.m = size(S, 1);
5.sample = [];
6.for i = 1:num
7.    x = ceil(rand()*m+1);
8.    sample = [sample; S(x, :)];
9.end
10.fprintf('******End of sampling******\n');
11.end

实验分析

由于图片数据量过大，且随着训练集规模增大，SMO算法训练时间成几何级数增长，（本人亲自测试：100个训练样本需要12.804秒，200个训练样本需要18.629秒，500个训练样本需要63.768秒，700个训练样本需要114.106秒，1000个训练样本需要248.256秒，1500个训练样本需要），绘制成以下曲线，可以看出训练时间随着训练样本大致呈现指数分布，因此用SMO算法跑60000张图片是不现实的；

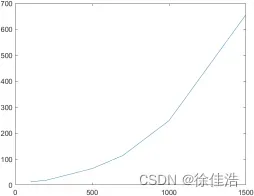
考虑到，SVM最终超平面其实是由支持向量进行决定的，因此我采取对训练集进行随机采样的方式，从60000随机抽取6000张图片进行训练，这样有效降低了训练规模大小，且最终训练结果也相当可靠，因为6000张将会有很大概率包含多个支持向量；

2.SVM主要核心为，SMO算法，该算法包含以下超参数：核函数类型（线性核函数，RBF核函数，高斯核函数，其中高斯核函数）、高斯核函数方差、惩罚系数C 、最大精度tol 、最大迭代次数 max_passes；我们通过调整上述参数使得SMO算法在训练集正确率与测试集正确率上取得好的效果；通过本人一遍遍探索，最终确定：核函数选取高斯核函数，高斯核函数方差=900 ，惩罚系数 C=1，最大精度tol=0.001 ，最大迭代次数max_passes=5 时在训练集与测试集均能取得良好效果：训练集正确率为98.65%，测试集正确率为93.00%；因为该方法每次使用的训练集均为随机采样的，选取优化变量具有一定随机性，因此每次结果都会有一定波动，但是总体而言还是比较稳定的，基本稳定在90%左右；

3.其中对于高斯核函数方差，该值的取值与样本在特征空间分布有一定关系，一开始我是将方差=0.01 ，但是其测试集准确率始终在10%左右，查看相关变量发现，每个样本在不同分类模型中得分都相等，这可能是因为取值过小导致了值太大导致溢出，因此我将方差值增大，随着方差值增大，测试集准确率也随之上升，方差取到900以上测试集正确率达到90%以上；为了探究取值到底与什么因素相关，我用IRIS数据集测试，发现方差=1是最佳的，通过分析样本在特征空间中的取值大小，MNIST数据集特征的值分布大致为200左右，IRIS特征的值分布大致为0.1左右，因此可以断言将会与数据集特征的值的分布相关，当样本在特征空间取值越大时，方差的取值也应当越大，数量级应当是相等的；

完整代码

test.m（训练与测试代码）

1.clc, clear
2.%导入训练集测试集
3.%每一行代表一个样本，第一列是标签值，剩余列是图片数据
4.train_filename = 'mnist_train.csv';
5.test_filename = 'mnist_test.csv';
6.train_set = csvread(train_filename);
7.test_set = csvread(test_filename);
8.
9.%train_set = train_set(1:6000, :);
10.N = 1500; %样本大小
11.train_set = sampling(train_set, N);
12.%将训练集分为标签与特征
13.y_train = train_set(:, 1);
14.x_train = train_set(:, 2:end);
15.
16.%训练集大小
17.m = size(x_train, 1);
18.n = size(x_train, 2);
19.
20.x_set = x_train;
21.y_set = zeros(m ,1);
22.C = 1;
23.tol = 1e-3;
24.sigmod = 1000;
25.max_itera = 10;
26.model_sum = [];
27.fprintf('******Begin to train******\n\n');
28.for i = 1:10
29.    fprintf('the %d kind train\n', i);
30.    for j = 1:m
31.        if y_train(j, 1) == i-1
32.            y_set(j, 1) = 1;
33.        else
34.            y_set(j, 1) = 0;
35.        end
36.    end
37.    %[w(:, i), b(:, i)] = smo_std(x_set, y_set, C, @gussian, tol, max_itera);    
38.    model = smo_quick2(x_set, y_set, C, @(x1, x2)gussianKernel(x1, x2, sigmod));
39.    %model = smo_quick2(x_set, y_set, C, @linearKernel);
40.    model_sum = [model_sum; model];
41.end
42.fprintf('******Finished training******\n');
43.
44.true = 0;
45.label_train = [];
46.score_sum = [];
47.for i = 1:10
48.    score = svmPredict(model_sum(i), x_set);
49.    score_sum = [score_sum, score];
50.end
51.[max_s, index] = max(score_sum, [], 2);
52.index = index-1;
53.for i = 1:m
54.    if index(i) == y_train(i)
55.        true = true+1;
56.    end
57.end
58.train_true_rate = true/m*100
59.
60.
61.%测试集上
62.%test_set = test_set(1:300, :);
63.test_set = sampling(test_set, ceil(N/10));
64.test_label = test_set(:, 1);
65.test_feature = test_set(:, 2:end);
66.label_test = [];
67.true = 0;
68.score_sum = [];
69.for i = 1:10
70.    score = svmPredict(model_sum(i), test_feature);
71.    score_sum = [score_sum, score];
72.end
73.[max_s, index] = max(score_sum, [], 2);
74.index = index-1;
75.for i = 1:size(test_feature, 1)
76.    if index(i) == test_label(i)
77.        true = true+1;
78.    end
79.end
80.test_true_rate = true/size(test_feature, 1)*100

smo_quick2.m（SMO算法实现）

159.function [model] = smo_quick2(X, Y, C, kernelFunction, tol, max_passes)
160.%smo_quick:加速版smo算法
161.%X:样本特征集，每一行代表一个样本
162.%Y：二分类标签集，正类为1，负类为0
163.%C：惩罚系数
164.%kernelFunction：所选核函数
165.%tol：判断相等的最大容忍值
166.%max_passes：没有alphas改变的最大迭代数
167.
168.%缺省处理方式
169.if ~exist('tol', 'var') || isempty(tol)
170.    tol = 1e-3;
171.end
172.if ~exist('max_passes', 'var') || isempty(max_passes)
173.    max_passes = 5;
174.end
175.
176.% 一些关于数据集的参数
177.m = size(X, 1);
178.n = size(X, 2);
179.
180.
181.Y(Y==0) = -1;
182.
183.% smo算法需要用的变量
184.alphas = zeros(m, 1);
185.b = 0;
186.E = zeros(m, 1);
187.passes = 0;
188.eta = 0;
189.L = 0;
190.H = 0;
191.
192.%根据所选核函数，计算Kernel矩阵
193.fprintf('******Begin to calculate Kernel mat******\n');
194.if strcmp(func2str(kernelFunction), 'linearKernel')
195.    %线性核
196.    K = X*X';
197.elseif strfind(func2str(kernelFunction), 'gaussianKernel')
198.   %RBF核
199.    X2 = sum(X.^2, 2);
200.    K = bsxfun(@plus, X2, bsxfun(@plus, X2', - 2 * (X * X')));
201.    K = kernelFunction(1, 0) .^ K;
202.else
203.    %高斯核
204.    K = zeros(m);
205.    for i = 1:m
206.        for j = i:m
207.             K(i,j) = kernelFunction(X(i,:)', X(j,:)');
208.             K(j,i) = K(i,j); %the matrix is symmetric
209.        end
210.    end
211.end
212.fprintf('******End of Kernel mat******\n');
213.% Train
214.fprintf('******Training******\n');
215.while passes < max_passes
216.    fprintf('******running now******\n');
217.    num_changed_alphas = 0;
218.    for i = 1:m
219.        E(i) = b + sum (alphas.*Y.*K(:,i)) - Y(i);
220.        %选择不满足KKT条件的alpha
221.        if ((Y(i)*E(i) < -tol && alphas(i) < C) || (Y(i)*E(i) > tol && alphas(i) > 0))
222.            %选择Ei-Ej绝对值最大的j
223.            non_zero_index = find(E ~= 0);
224.            num_E_nozero = length(non_zero_index);
225.            j = -1; max_E = 0;
226.            if num_E_nozero > 1
227.                for k = (non_zero_index)'
228.                    if k == i
229.                        continue;
230.                    end
231.                    Ek = b + sum (alphas.*Y.*K(:,k)) - Y(k);
232.                    deltaE = abs(Ek-E(i));
233.                    if deltaE >= max_E
234.                        max_E = deltaE;
235.                        j = k;
236.                    end
237.                end
238.            else
239.                j = ceil(m * rand());
240.                while j == i  
241.                    j = ceil(m * rand());
242.                end
243.            end                       
244.            E(j) = b + sum (alphas.*Y.*K(:,j)) - Y(j);            
245.            % Save old alphas
246.            alpha_i_old = alphas(i);
247.            alpha_j_old = alphas(j);            
248.            % Compute L and H by (10) or (11). 
249.            if (Y(i) == Y(j))
250.                L = max(0, alphas(j) + alphas(i) - C);
251.                H = min(C, alphas(j) + alphas(i));
252.            else
253.                L = max(0, alphas(j) - alphas(i));
254.                H = min(C, C + alphas(j) - alphas(i));
255.            end         
256.            if (L == H)
257.                % continue to next i. 
258.                %fprintf('******L=H******\n');
259.                continue;
260.            end
261.            % Compute eta by (14).
262.            eta = 2 * K(i,j) - K(i,i) - K(j,j);
263.            if (eta >= 0)
264.                % continue to next i. 
265.                fprintf('******eta>=0******\n');
266.                continue;
267.            end            
268.            % Compute and clip new value for alpha j using (12) and (15).
269.            alphas(j) = alphas(j) - (Y(j) * (E(i) - E(j))) / eta;
270.            fprintf('******New the alphas******\n');
271.            % Clip
272.            alphas(j) = min (H, alphas(j));
273.            alphas(j) = max (L, alphas(j));  
274.            E(j) = b + sum (alphas.*Y.*K(:,j)) - Y(j);
275.            % Check if change in alpha is significant
276.            if (abs(alphas(j) - alpha_j_old) < tol)
277.                fprintf('******old_alphaj=new_alphaj******\n');
278.                alphas(j) = alpha_j_old;
279.                continue;
280.            end
281.            % Determine value for alpha i using (16). 
282.            alphas(i) = alphas(i) + Y(i)*Y(j)*(alpha_j_old - alphas(j));
283.            E(i) = b + sum (alphas.*Y.*K(:,i)) - Y(i);
284.            % Compute b1 and b2 using (17) and (18) respectively. 
285.            b1 = b - E(i) ...
286.                 - Y(i) * (alphas(i) - alpha_i_old) *  K(i,j)' ...
287.                 - Y(j) * (alphas(j) - alpha_j_old) *  K(i,j)';
288.            b2 = b - E(j) ...
289.                 - Y(i) * (alphas(i) - alpha_i_old) *  K(i,j)' ...
290.                 - Y(j) * (alphas(j) - alpha_j_old) *  K(j,j)';
291.            if (0 < alphas(i) && alphas(i) < C)
292.                b = b1;
293.            elseif (0 < alphas(j) && alphas(j) < C)
294.                b = b2;
295.            else
296.                b = (b1+b2)/2;
297.            end
298.            num_changed_alphas = num_changed_alphas + 1;
299.        end        
300.    end    
301.    if (num_changed_alphas == 0)
302.        passes = passes + 1;
303.    else
304.        passes = 0;
305.    end
306.end
307.fprintf(' Done! \n\n');
308.% Save the model
309.idx = alphas > 0;
310.model.X= X(idx,:);
311.model.y= Y(idx);
312.model.kernelFunction = kernelFunction;
313.model.b= b;
314.model.alphas= alphas(idx);
315.model.w = ((alphas.*Y)'*X)';
316.End

svmPredict.m（输出预测值的函数）

48.function p = svmPredict(model, X)
49.%SVMPREDICT returns a vector of predictions using a trained SVM model
50.%(svmTrain). 
51.%   pred = SVMPREDICT(model, X) returns a vector of predictions using a 
52.%   trained SVM model (svmTrain). X is a mxn matrix where there each 
53.%   example is a row. model is a svm model returned from svmTrain.
54.%   predictions pred is a m x 1 column of predictions of {0, 1} values.
55.%
56.
57.% Check if we are getting a column vector, if so, then assume that we only
58.% need to do prediction for a single example
59.if (size(X, 2) == 1)
60.    % Examples should be in rows
61.    X = X';
62.end
63.
64.% Dataset 
65.m = size(X, 1);
66.p = zeros(m, 1);
67.pred = zeros(m, 1);
68.
69.if strcmp(func2str(model.kernelFunction), 'linearKernel')
70.    % We can use the weights and bias directly if working with the 
71.    % linear kernel
72.    p = X * model.w + model.b;
73.elseif strfind(func2str(model.kernelFunction), 'gaussianKernel')
74.    % Vectorized RBF Kernel
75.    % This is equivalent to computing the kernel on every pair of examples
76.    X1 = sum(X.^2, 2);
77.    X2 = sum(model.X.^2, 2)';
78.    K = bsxfun(@plus, X1, bsxfun(@plus, X2, - 2 * X * model.X'));
79.    K = model.kernelFunction(1, 0) .^ K;
80.    K = bsxfun(@times, model.y', K);
81.    K = bsxfun(@times, model.alphas', K);
82.    p = sum(K, 2);
83.else
84.    % Other Non-linear kernel
85.    for i = 1:m
86.        prediction = 0;
87.        for j = 1:size(model.X, 1)
88.            prediction = prediction + ...
89.                model.alphas(j) * model.y(j) * ...
90.                model.kernelFunction(X(i,:)', model.X(j,:)');
91.        end
92.        p(i) = prediction + model.b;
93.    end
94.end
95.
96.% Convert predictions into 0 / 1
97.pred(p >= 0) =  1;
98.pred(p <  0) =  0;
99.
100.end

gussianFunction.m（高斯核函数）

24.function sim = gaussianKernel(x1, x2, sigma)
25.%RBFKERNEL returns a radial basis function kernel between x1 and x2
26.%   sim = gaussianKernel(x1, x2) returns a gaussian kernel between x1 and x2
27.%   and returns the value in sim
28.
29.% Ensure that x1 and x2 are column vectors
30.x1 = x1(:); x2 = x2(:);
31.
32.% You need to return the following variables correctly.
33.sim = 0;
34.
35.% ====================== YOUR CODE HERE ======================
36.% Instructions: Fill in this function to return the similarity between x1
37.%               and x2 computed using a Gaussian kernel with bandwidth
38.%               sigma
39.%
40.%
41.
42.sim=(x1-x2)'*(x1-x2);
43.sim=exp(-sim/(2*sigma^2));
44.% =============================================================
45.    
46.end

sampling.m（随机采样）

12.function sample = sampling(S, num)
13.%sampling：在S中随机选择num个样本
14.fprintf('******Begin to sampling******\n');
15.m = size(S, 1);
16.sample = [];
17.for i = 1:num
18.    x = ceil(rand()*m+1);
19.    sample = [sample; S(x, :)];
20.end
21.fprintf('******End of sampling******\n');
22.end

总结

本文借鉴《统计学习基础》以及《机器学习实战》

通过此次学习，有以下几点收获：

（1）编写代码前先得写伪代码，并根据伪代码进行算法编写，这样能使得编代码时思路清晰明了；

（2）编写代码前得对其总体结构有清楚认识，可以列个大纲之类的，将任务模块化；

（3）函数传入参数尽量要少，将尽可能多的工作放在函数内部去做；

（4）将参数写在一块，方便之后调试；

（5）吸纳别人经验，可以有效拓宽视野，更快找到问题所在；

文章出处登录后可见！

已经登录？立即刷新

基于SVM的手写数字识别

前言