ICLR 2023
1 intro
- 时间序列一般是连续记录的,每个时刻只会记录一些标量
- 之前的很多工作着眼于时间维度的变化,以捕捉时间依赖关系
- ——>可以反映出、提取出时间序列的很多内在特征,比如连续性、趋势、周期性等
- 但是现实时间序列数据中的时间序列通常是由很复杂的时间特征组成,不同的时间维度上的变化会糅杂在一起,使得建模时间维度的变化异常困难
- 之前的很多工作着眼于时间维度的变化,以捕捉时间依赖关系
- 在深度学习领域,很多模型有很强的建模非线性的能力,因而可以捕获时间序列中一些复杂的时间维度变化。但是他们各有一些弊端
- RNN:基于马尔可夫假设(t-1时刻的观测影响t时刻的预测),建模连续时刻的时间序列特征
- 这类方法经常难以建模长期时间依赖性
- 同时由于不能并行,效率堪忧
- TCN:在时间维度上使用卷积神经网络
- 由于时间序列的一维邻接关系,TCN只能建模时间维度上相近时刻的时间序列特征
- ——>仍然无法建模长期时间依赖关系
- Transformer,self-attention
- 仅仅使用各离散时刻时间序列观测值之前的点积关系,可能获得的并不一定是实际的相互依赖关系
- RNN:基于马尔可夫假设(t-1时刻的观测影响t时刻的预测),建模连续时刻的时间序列特征
- 这篇paper从多周期的角度观测时间序列
- 时间序列通常呈现出多周期
- 比如天气数据可能有日周期和年周期
- 电力消费数据可能有周周期和季度周期
- 对每个周期来说,每个时刻时间序列的观测值不仅由相邻区域的时间特征影响,还由邻接周期相应位置的时间特征决定
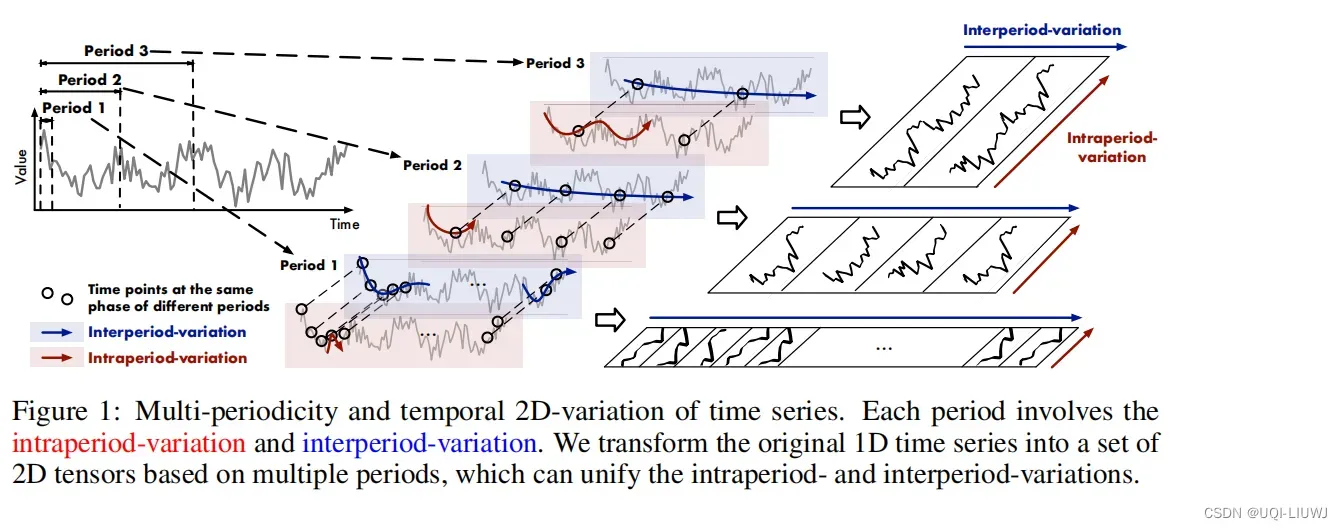
- 论文中称之为 intraperiod-variation(周期内变化)、interperiod-variation(周期间变化)
- 周期内变化表示一个周期内的短期时间特征
- 周期间变化表示周期间的长期时间特征
- 如果一个时间序列没有周期性,那可以认为他的周期是无穷大,他的时间特征仅有周期内变化决定
- 时间序列通常呈现出多周期
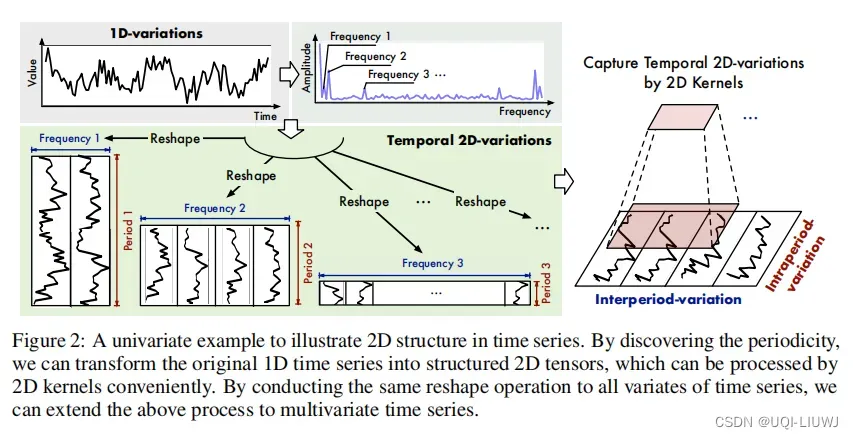
- 一维时间序列很难显示地表示两种不同的时间维度变化
- ——>论文将一维时间序列reshape到一组二维的张量,其中每一个张量的列表示一个周期,行表示不同周期内同一对应位置(同一相位)
- 这样reshape之后,周期内和周期间的时间依赖关系都能够很好地建模了
- 每一列相邻的元素表示邻接时间序列之前的时间依赖关系;每一行相邻元素表示的是不同周期同一相位之前的时间依赖关系
-
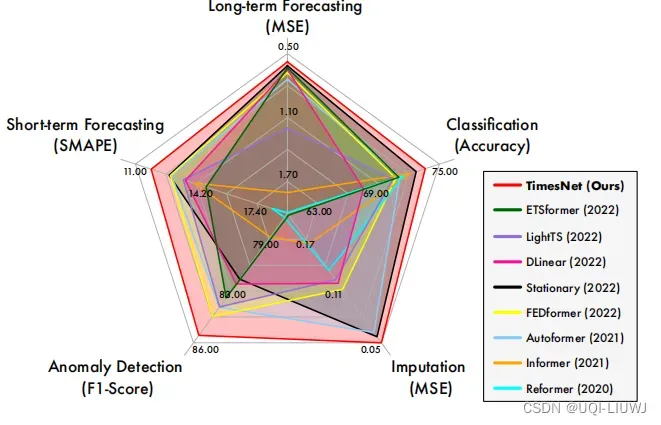
- 基于上面的一维时间序列到二维张量的变化,作者提出了TimesNet,实验表明其在长期/短期时间序列预测、时间序列补全、时间序列分类、时间序列异常检测任务中都有不俗的表现
- 同时,TimesNet考虑并解耦了多周期时间序列特征,可以更好地表征时间序列
2 TImesNet
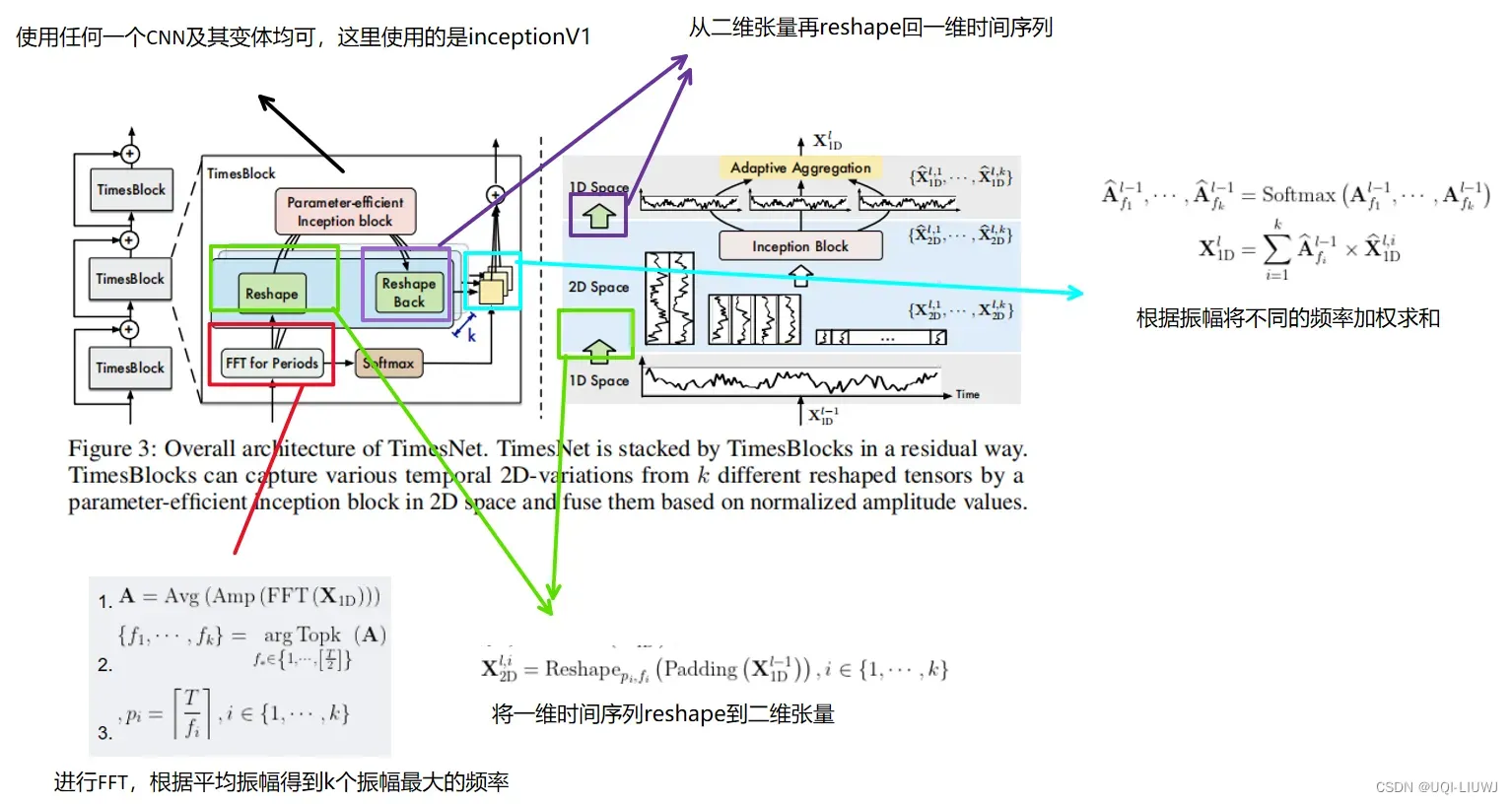
2.1 从一维时间序列到二维张量的转化
可以用如下三个公式表示
- 式1
- FFT(.)表示将一维时间序列进行快速傅里叶变化(个人理解就是将N长的时域信号转换为N/2长度的谱域信号)
- Amp就是算各个时间序列转换后,在各个频率上的振幅
- Avg就是对不同时间序列的振幅求平均
- —>A是不同频率的平均振幅
- 式2
- 取平均振幅最大的k个频率
- 式3
- 得到对应的k个周期
- 为了简便考虑,论文将上述三个式子简化成:
基于,可以将一维时间序列
转化成一组二维张量
,其中第i个二维张量
的计算方式为:
- 这里Padding的作用是在时间序列末端补0,使得正好能Reshape到二维张量
2.2 TimesBlock
- 这里使用了残差连接
- 对于输入
- 第一层
是通过直接喂入embedding层得到的
- 之后的每一层,输入是
,输出是
- 对于输入
2.2.1 捕获2D时间维度变化
- 第一行:根据上一个TimesBlock的输出,得到对应的平均振幅,振幅最大的k个频率和对应的周期
- 第二行,根据这k个频率,将一维时间序列reshape到不同的二维张量中
- 第三行,这里使用的是inception v1 机器学习笔记:inceptionV1 inceptionV2_机器学习inception_UQI-LIUWJ的博客-CSDN博客,当然别的CNN衍生模型也可以
- 第四行,将inception学到的二维表征
重新reshape回一维时间序列
- 使用Trunc将时间序列长度放缩到原来的T
2.2.2 自适应加和
- 在上一步中,我们得到了
,那怎么将他们结合呢?
- 根据第一行得到的平均振幅,进行softmax得到对应的权重,将这k项进行加权求和
3 实验
3.1 数据集
论文比较了长期时间序列预测、短期时间序列预测、时间序列补全、时间序列分类、异常检测五个问题
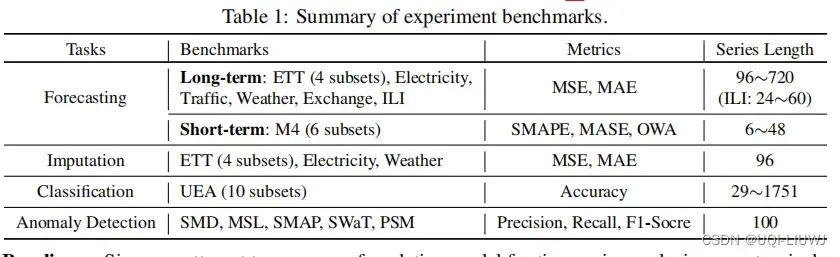

3.2 主要结果
3.2.1 短期时间序列预测
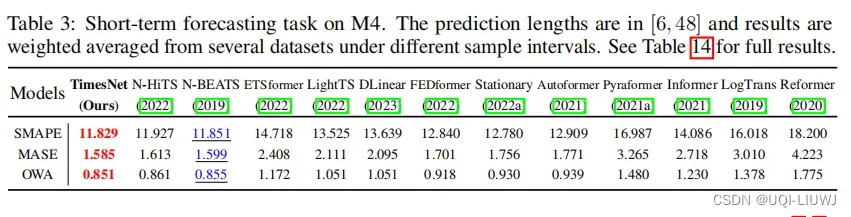
3.2.2 长期时间序列预测

3.2.3 时间序列补全

3.2.4 时间序列分类
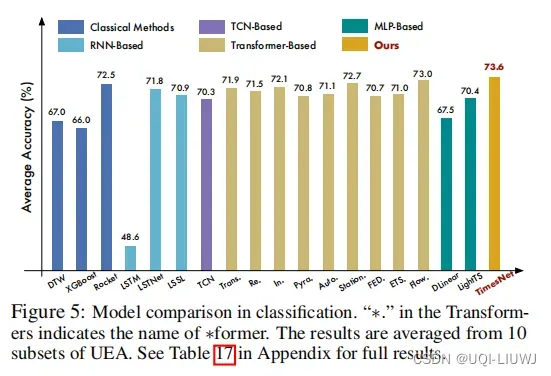
3.2.5 时间序列异常检测
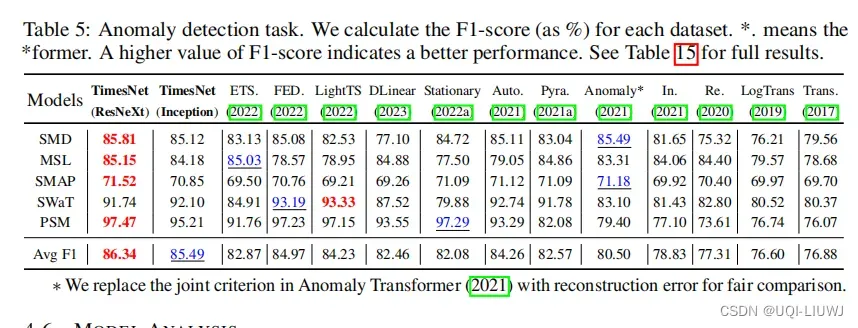
3.3 2D时间序列张量可视化
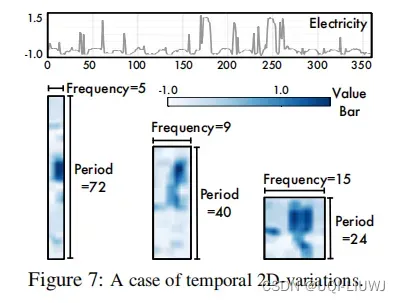
3.4 超参数稳定性
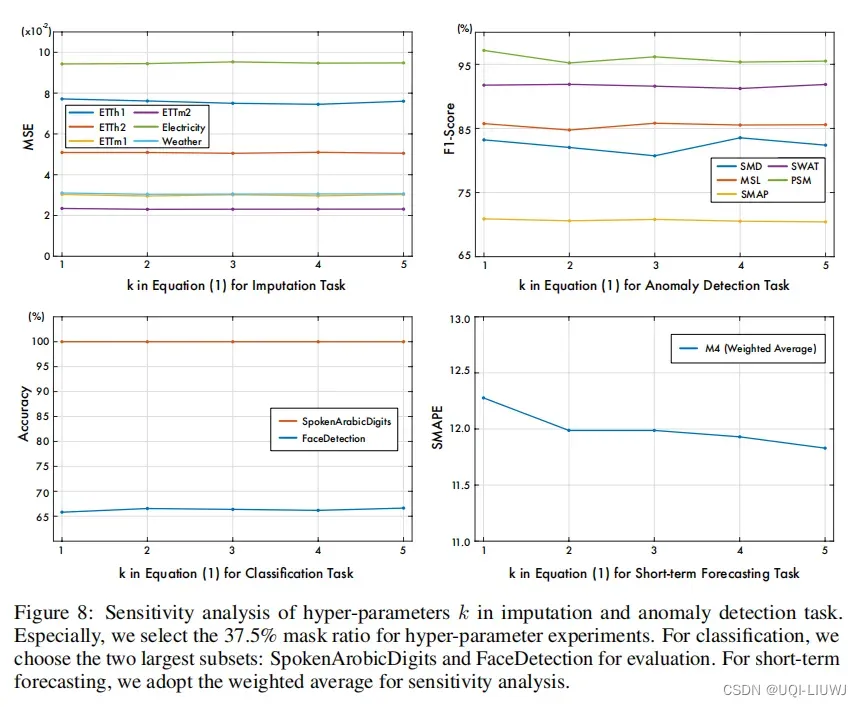
- 基本上都是稳定的,不过对预测和异常检测来说,k的选择会影响到最终的表现。
3.5 消融实验
3.5.1 不用Inception,使用别的卷积架构
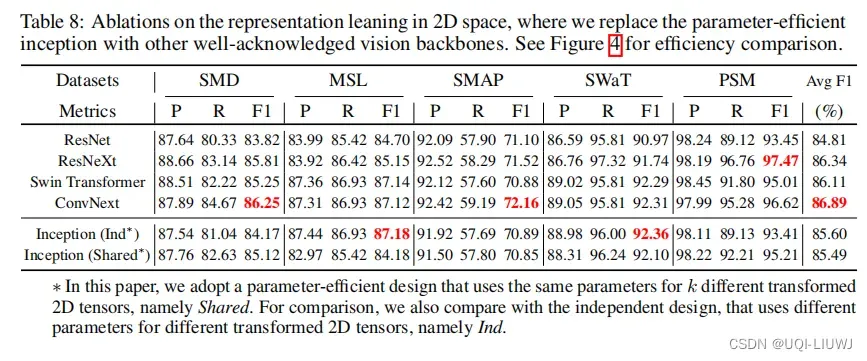
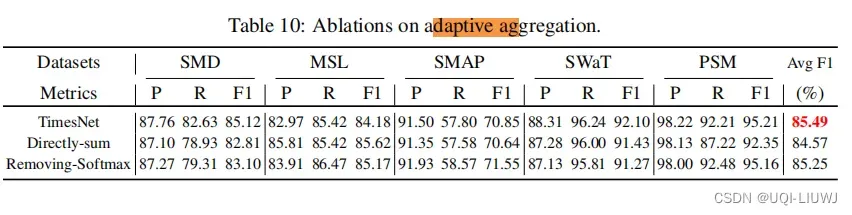
3.5.2 自适应加和部分
- directly-sum:把得到的
直接求和
- removing-sum:不用Softmax,直接
3.6 regression效果可视化
3.6.1 imputation
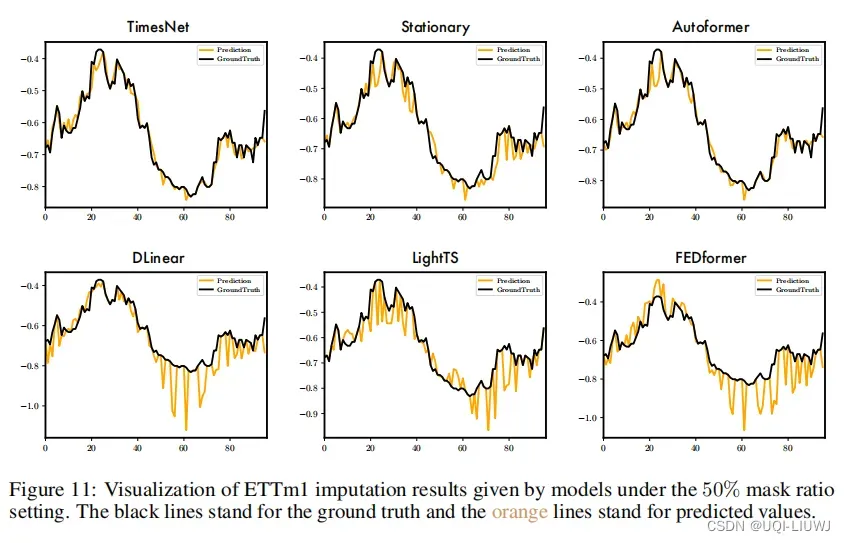
3.6.2 prediction
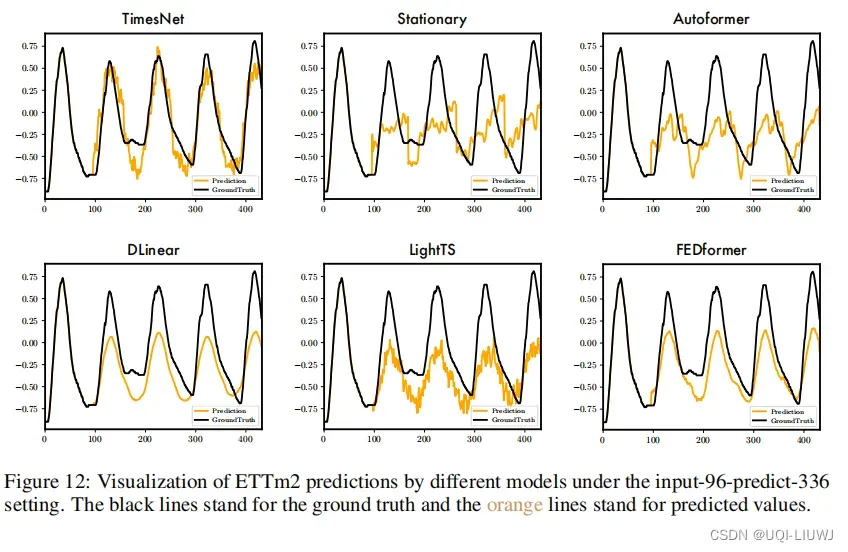
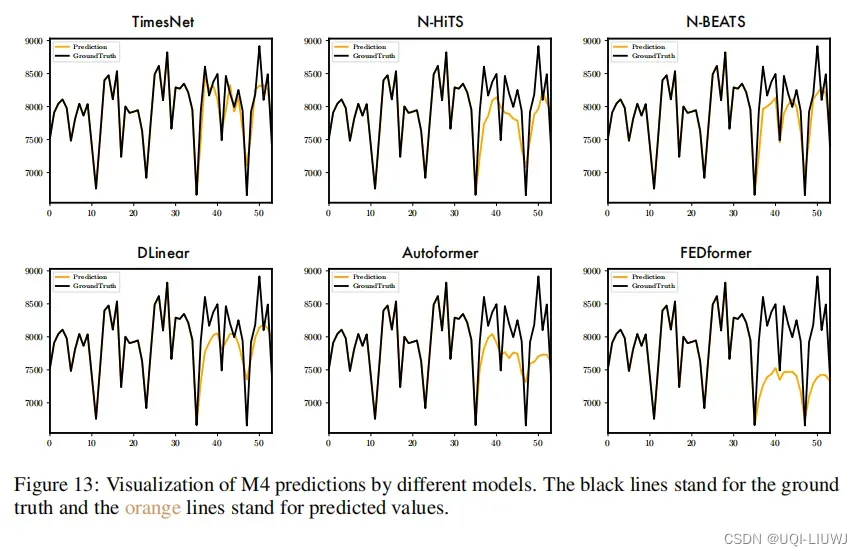
文章出处登录后可见!
已经登录?立即刷新
