集合卡尔曼滤波（EnKF）原理及样例应用

EnKF 是一种基于蒙特卡罗方法预测误差统计信息的卡尔曼滤波。它与 PF 的相同点是都采用了采样粒子的集合来表示状态概率空间，但 EnKF 在更新步使用卡尔曼更新，该方法以集合的形式进行模拟预报和 分析更新这两个过程,通过模式状态的集合来表征 误差协方差的信息,以最小化观测值和模拟值的误 差协方差为约束条件,对目标进行最优估计。

了解其基本思路，为便于理解，我们对该过程拆分简化为以下几个流程：

1. 初始化：初始化系统状态变量 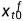，初始误差协方差矩阵 和初始状态预测集合 { }

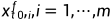2. 数据同化：时刻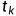,我们分别进行观测步、分析步、预测步，具体流程如下：

a.观测步：

1. 计算观测集合：

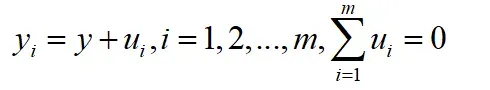
2. 计算观测误差协方差矩阵:

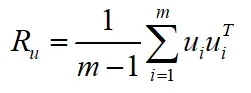
b.分析步:

3. 计算卡尔曼增益矩阵：

4. 计算分析集合:

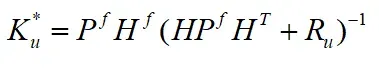
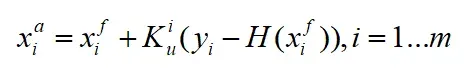
5. 计算分析集合均值：

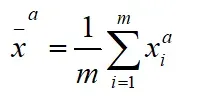
6. 计算分析误差协方差矩阵：

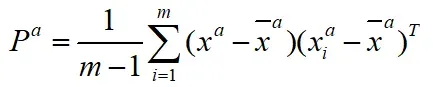
c.预测步:

7. 计算预测集合：

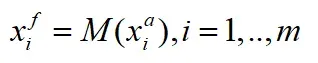
8. 计算预测集合均值:

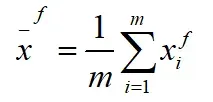
9. 计算预测误差协方差矩阵：

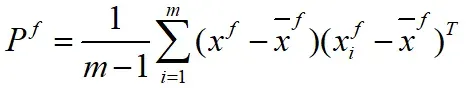
对EnKF算法原理了解之后，我们进入一个简单问题的实战(基于python):

考虑离散模型：

显然，这是如下的一维谐振子的数值实现：

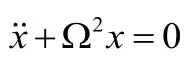
这是一个离散的二阶方程，上式中x的系数与成比例。因此，状态向量有两个输入。

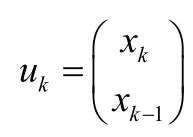
预解矩阵是：

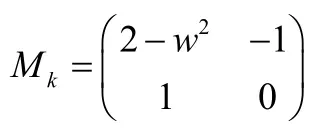
对任意有,观测算子为，观测方程为：

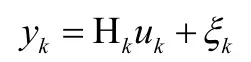
在高斯白噪声方差为 g 的情况下。这个方差的值应该是已知的。观测结果可能不是在每个时间步骤上都能得到的。

接下来进入代码运行环节：

相关函数定义

# 导入相关库
import numpy as np
import pandas as pd
import seaborn as sn
import warnings
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['KaiTi']     
plt.rcParams['axes.unicode_minus'] = False
from scipy.linalg import fractional_matrix_power
np.random.seed(None)
warnings.filterwarnings("ignore")

def EnKF(u0_f, P0_f, T, delta, H, X, lam, m): # EnKF函数定义
    X_f = [float(u0_f[1][0]), float(u0_f[0][0])]
    X_a = [float(u0_f[1][0])]
    Y = []
    u_f = np.matrix([[X_f[1]], [X_f[0]]])
    r = 100  # 生成集合的方差
    u1 = mean(float(u0_f[0][0]), r, m)
    u2 = mean(float(u0_f[1][0]), r, m)
    U_f = []
    for i in range(m):
        U_f.append(np.matrix([[u1[i]], [u2[i]]]))
    for i in range(1, T + 1):  # 迭代运算
        if i % delta == 0:  # 带有观测值时的情况
            # 计算增益
            r = mean(0, 1, m)
            y = X[i] + r
            r = np.matrix(r)
            u = np.matrix([[X[i]], [X[i - 1]]])
            R = float(r * r.T)  # 观测误差方差
            K = P0_f * H.T * (H * P0_f * H.T + R).I
            Y.append(X[i])
            U_a = []  # 初始化ua_i
            for j in range(m):
                U_a.append(U_f[j] + K * (y[j] - H * U_f[j]))
            u_a = sum(U_a) / m
            X_a.append(float(u_a[0][0]))
            # 预测步骤
            ind = i // delta
            M = matrix(w, lam, X_a[ind])
            for j in range(m):
                U_f[j] = M * U_a[j]
            u_f = sum(U_f) / m
            P0_f = 0
            for j in range(m):
                P0_f += (U_f[j] - u_f) * (U_f[j] - u_f).T
            P0_f = P0_f / (m - 1)

        else:  # 不带有观测值的情况，此时只预测
            M = matrix(w, lam, X_f[i])
            for j in range(m):
                U_f[j] = M * U_f[j]
            u_f = sum(U_f) / m
            P0_f = 0
            for j in range(m):
                P0_f += (U_f[j] - u_f) * (U_f[j] - u_f).T
            P0_f = P0_f / (m - 1)
        X_f.append(float(u_f[0][0]))
    return X_f, Y

def mean(j,r,m):  #定义固定均值的正态分布
    u = np.random.normal(j,r,m)
    s = sum(u)/m
    return u+(j-1*s)

def matrix(w,lam,x): #定义预解矩阵
    return np.matrix([[2+(w**2)-(lam**2) * (x**2),-1],[1,0]])

问题分析

# 初始化系统状态与误差协方差矩阵
u0_f = np.matrix([[1],[0]])
P0_f = np.array([[0.3, 0], [0, 0.3]])

# 预解矩阵
w = 0.035
lam = 0.0003
H = np.matrix([1,0]) # 观测算子
X = [0,1]

# 时间与时间间隔(步长)
T = 1000
delta = 25

for i in range(2,T+2):
    X.append((2+w**2)*X[i-1]-(lam**2)*X[i-1]**3-X[i-2])
    
m =50 # 定义集合的大小

X_f,Y = EnKF(u0_f,P0_f,T,delta,H,X,lam,m)

可视化展示

plt.plot(range(T+2), X, c='Lime', label="实际曲线")
plt.plot(range(T+2), X_f, c="g", linestyle='dashed',label="拟合曲线")
plt.scatter(list(range(delta,T+1,delta)), np.array(Y), c='r', label="观测值")
plt.legend()
plt.title("EnKF")
plt.show()
plt.savefig('EnKF.png')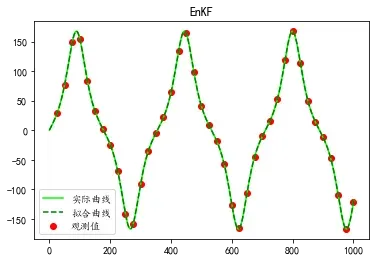

以上即为EnKF算法的原理分析及简单实战，学海无涯，让我们继续一同探索吧！