Pearson相关系数和Spearman相关系数的区别
参考资料前两个博客讲解的非常详细,因本人想要自己梳理下,才有此文,请直接跳转即可。
1、协方差、相关系数
(1)简单来说
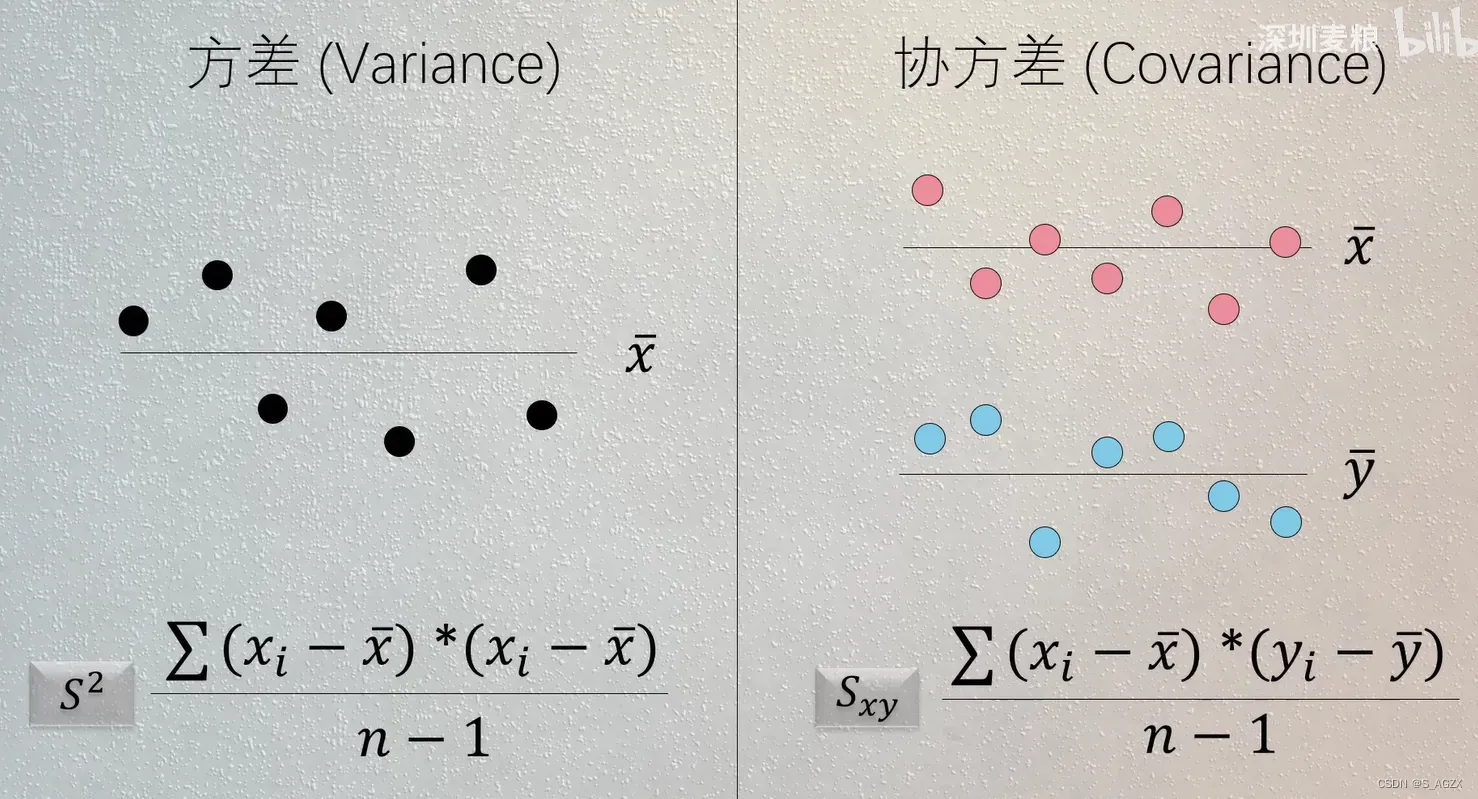
协方差:变量具有 同增、同减 的趋势。趋势越接近,则相关性越大,反之越小。
相关系数:协方差的标准化,把数值控制在[-1,1]的区间表示。方便比较多组变量的相关性强弱。
(2)作用上来说
协方差描述两个变量之间相关的 方向,相关系数解释相关的 强度。
(3)复杂点说:协方差是随机变量离差之积,与随机变量分布函数乘积的积分,或者是就是离差乘积的期望。
(4)相关系数范围
相关系数是用以反映变量之间的相关关系程度的统计指标。其取值范围是[-1,1],当取值为0时表示不相关,取值为[-1,0)表示负相关,取值为(0,-1],表示负相关。
方差与协方差的区别:
参考视频:十分钟理解协方差和相关系数、如何通俗地解释协方差
2、Pearson相关系数
皮尔森相关系数评估两个连续变量之间的 线性关系,是用来衡量两个数据集的线性相关程度。
数据集要 符合正态分布、无异常值、连续变量 等特定。
3、Spearman相关系数
3.1 定义
斯皮尔曼相关系数评估两个连续变量之间的单调关系。在单调关系中,变量趋于一起变化,但不一定以恒定速率变化。
它也被称为等级相关或者秩相关(即rank)。
3.2 什么时候用
当 (1)分布严重非正态;(2)变量非连续;(3)异常值影响大, 的时候,要舍弃Pearson相关系数。
4、两者的区别点
4.1 线性相关与单调相关
Pearson相关系数是用来衡量两个数据集(变量)的线性相关程度。而Spearman相关系数不关心两个数据集是否线性相关,而是单调相关。
在单调关系中,变量倾向于沿着相同的相对方向移动,但不一定以恒定的速率移动。在线性关系中,变量沿着相同的方向以恒定的速率移动。
4.2 前提假设不同
Pearson相关假设数据集在同一条直线上,而Spearman只要求单调递增或者递减,所以Pearson的统计效力比Spearman要高。
更重要的是,要根据实际情况选择正确的假设。
比如,某个实验做了两次技术或者生物学重复,那有理由假设这两次重复线性相关。而如果是一个基因和另一个受到调控的基因的表达水平,或者某个基因顺式作用元件的染色质开放程度,和这个基因表达水平之间的关系就可能只需要假设单调相关。
4.3 变量正态分布与否
Pearson相关系数要求数据集是连续型变量,并且符合正态分布,而Spearman相关系数没有这个要求;
Pearson相关系数在出现奇异值,或者长尾分布的时候稳定性差,不太可靠,而Spearman对于数据错误和极端值的反应不敏感。
5、实例展示
(1)上面两张图
如果对数据进行线性变换(y = ax + b; a ≠ 0),两者相关系数的绝对值都不会发生变化(要考虑下正负);
上面两个图既是单调关系,也是线性关系。
(2)中间两张图
如果对数据进行单调但不线性的变换(比如最常见的log scale),Spearman相关系数的绝对值也不会发生变化。
两张图显示两个变量同时上升,但不以相同的速率上升。此关系是单调的,但不是线性的。
(3)下面两张图
左下图显示了当关系是随机的或不存在时,则两个相关系数几乎为零。
右下图显示了非常强的关系。Pearson系数和Spearman系数均约为0。
6、参考资料
1、Pearson相关系数和Spearman相关系数的区别
2、救救孩子!Spearman、Pearson相关系数傻傻分不清?
3、统计学与质量051 – 相关性 – 自变量与因变量 协方差(Covariance)
4、统计学与质量052 – 皮尔逊 (Pearson) 相关系数 & 斯皮尔曼 (Spearman)相关系数
文章出处登录后可见!