简述随机游走模型
一维随机游走问题:设一个质点(随机游走者)沿着一条直线运动,单位时间内只能运动一个单位长度,且只能停留在该直线上的整数点,假设在时刻t,该质点位于直线上的点i,那么在时刻t +1,该质点的位置有三种可能:
①以p 的概率跳到整数点i-1
②或以q的概率跳到点i+1
③或以r=1-p-q的概率继续停留在点i

由于每一步的结果都是独立的,且每种情况发生的概率之和都为1,则该过程服从伯努利分布,称为贝努利随机游走过程。当 p=q=0.5时,即质点在下一时刻到达其相邻点的概率是相等的,称为简单的随机游走。
基于随机游走的图像分割算法
随机游走算法是一种基于图论的分割算法,属于一种交互式的图像分割。它的分割思想是,以图像的像素为图的顶点,相邻像素之间的四邻域或八邻域关系为图的边,并根据像素属性及相邻像素之间特征的相似性定义图中各边的权值,以此构建网络图,然后由通过用户手工指定前景和背景标记,即前景物体和背景物体的种子像素,以边上的权重为转移概率,未标记像素节点为初始点,计算每个未标记节点首次到达各种子像素的概率,根据概率大小,划分未标记节点,得到最终分割结果。
以下内容来自参考文献:Grady L .Random Walks for Image Segmentation[J].IEEE Transactions on Pattern Analysis & Machine Intelligence, 2006, 28:1768-1783.DOI:10.1109/TPAMI.2006.233.
L1,L2,L3三个种子点分别由用户交互输入,作为标记的种子点。现要把图像分割成对应的三部分。
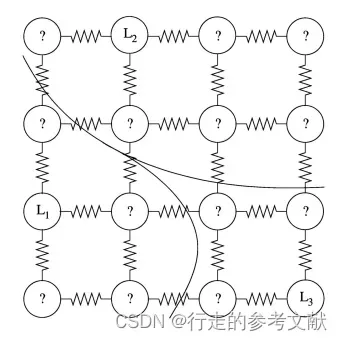
计算图中任意一点vi与其各个邻接顶点连接边的权重
对于图中任意一点vi的概率,其满足随机游走概率公式
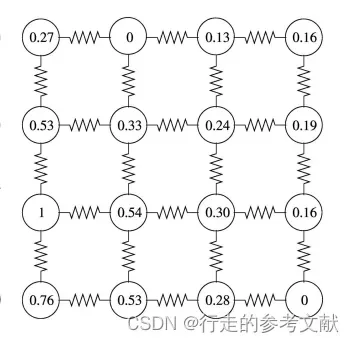
加边界约束条件:以已标记的K类顶点作为边界约束条件,求解各未知点游走到L1的概率,则以PL1=1,PL2=0,PL3=0,作为约束条件,可求得个未知点的概率,如下图所示:
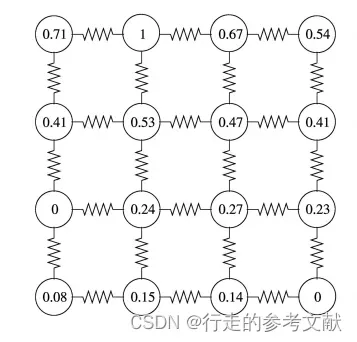
同理,到达L2的概率为
到达L3的概率为
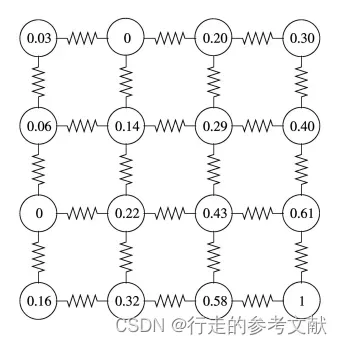
每一个未标记点,根据获得的对 K 类标记的隶属度值进行判断,若未标记点到达第k类的概率最大,则将未标记节点vi判别为属于类别k,完成分割。
python代码
import numpy as np import networkx as nx import random class Graph(): def __init__(self, nx_G, is_directed, p, q): self.G = nx_G self.is_directed = is_directed self.p = p self.q = q def node2vec_walk(self, walk_length, start_node): ''' Simulate a random walk starting from start node. ''' G = self.G alias_nodes = self.alias_nodes alias_edges = self.alias_edges walk = [start_node] while len(walk) < walk_length: cur = walk[-1] cur_nbrs = sorted(G.neighbors(cur)) if len(cur_nbrs) > 0: # 如果序列中仅有一个结点,即第一次游走 # alias_nodes中保存了alias_setup的[alias, accept],通过alias_draw返回采样的下一个索引号 if len(walk) == 1: walk.append(cur_nbrs[alias_draw(alias_nodes[cur][0], alias_nodes[cur][1])]) else: # 当前游走结点的前一个结点和下一个节点 prev = walk[-2] # 使用alias_edges中记录的[alias, accept],来采样邻居中的下一个节点 next = cur_nbrs[alias_draw(alias_edges[(prev, cur)][0], alias_edges[(prev, cur)][1])] walk.append(next) else: break return walk def simulate_walks(self, num_walks, walk_length): ''' Repeatedly simulate random walks from each node. ''' G = self.G walks = [] nodes = list(G.nodes()) # nodes采样一次为一个epoch,此处就是num_walks个epoch print('Walk iteration:') for walk_iter in range(num_walks): print(str(walk_iter+1), '/', str(num_walks)) random.shuffle(nodes) for node in nodes: walks.append(self.node2vec_walk(walk_length=walk_length, start_node=node)) return walks def get_alias_edge(self, src, dst): ''' Get the alias edge setup lists for a given edge. :return alias_setup(): 在上一次访问顶点 t ,当前访问顶点为 v 时到下一个顶点 x 的未归一化转移概率。 :param src: 随机游走序列种的上一个结点 :param dst: 当前结点 参数p控制重复访问刚刚访问过的顶点的概率。若p较大,则访问刚刚访问过的顶点的概率会变低。 参数q控制着游走是向外还是向内: 若q>1,随机游走倾向于访问和上一次的t接近的顶点(偏向BFS);若q<1,倾向于访问远离t的顶点(偏向DFS) ''' G = self.G p = self.p q = self.q unnormalized_probs = [] for dst_nbr in sorted(G.neighbors(dst)): if dst_nbr == src: unnormalized_probs.append(G[dst][dst_nbr]['weight']/p) elif G.has_edge(dst_nbr, src): unnormalized_probs.append(G[dst][dst_nbr]['weight']) else: unnormalized_probs.append(G[dst][dst_nbr]['weight']/q) norm_const = sum(unnormalized_probs) normalized_probs = [float(u_prob)/norm_const for u_prob in unnormalized_probs] return alias_setup(normalized_probs) def preprocess_transition_probs(self): ''' Preprocessing of transition probabilities for guiding the random walks. 用于引导随机游走的预处理,得到马尔可夫转移概率矩阵。 ''' G = self.G is_directed = self.is_directed alias_nodes = {} # G.neighbors(node) 与顶点相邻的所有顶点,更方便更快的访问adjacency字典用: G[cur] for node in G.nodes(): # 根据邻居节点的权重,计算转移概率 unnormalized_probs = [G[node][nbr]['weight'] for nbr in sorted(G.neighbors(node))] norm_const = sum(unnormalized_probs) # 计算当前节点到邻居节点的转移概率,其实就是权重归一化 normalized_probs = [float(u_prob)/norm_const for u_prob in unnormalized_probs] # 设置alias table,保存每个节点的accept[i]和alias[i],为后面alias采样做准备。 alias_nodes[node] = alias_setup(normalized_probs) alias_edges = {} triads = {} # 保存每条边的accept[i]和alias[i] if is_directed: for edge in G.edges(): alias_edges[edge] = self.get_alias_edge(edge[0], edge[1]) else: for edge in G.edges(): alias_edges[edge] = self.get_alias_edge(edge[0], edge[1]) alias_edges[(edge[1], edge[0])] = self.get_alias_edge(edge[1], edge[0]) self.alias_nodes = alias_nodes self.alias_edges = alias_edges return def alias_setup(probs): ''' Compute utility lists for non-uniform sampling from discrete distributions. Refer to https://hips.seas.harvard.edu/blog/2013/03/03/the-alias-method-efficient-sampling-with-many-discrete-outcomes/ for details :param probs: 指定的采样结果概率分布列表。期望按这个概率列表来采样每个随机变量X。 :return J: alias[i]表示第i列中不是事件i的另一个事件的编号。 :return p: accept[i]表示事件i占第i列矩形的面积的比例。 ''' K = len(probs) # q表示:accept数组 q = np.zeros(K) # J表示:alias数组 J = np.zeros(K, dtype=np.int) # Alias方法将整个概率分布压成一个 1*N 的矩形,每个事件转换为矩形中的面积。 # 将面积大于1的事件多出的面积补充到面积小于1对应的事件中,以确保每一个小方格的面积为1, # 同时,保证每一方格至多存储两个事件。 smaller = [] # 面积小于1的事件 larger = [] # 面积大于1的事件 for kk, prob in enumerate(probs): q[kk] = K*prob if q[kk] < 1.0: smaller.append(kk) else: larger.append(kk) while len(smaller) > 0 and len(larger) > 0: small = smaller.pop() large = larger.pop() J[small] = large # 其实是 q[large] - (1.0 - q[small]),把大的削去(1.0 - q[small])填充到小的上 q[large] = q[large] + q[small] - 1.0 # 大的剩下的面积,放到下一轮继续倒腾 if q[large] < 1.0: smaller.append(large) else: larger.append(large) return J, q def alias_draw(J, q): ''' Draw sample from a non-uniform discrete distribution using alias sampling. 参考:https://zhuanlan.zhihu.com/p/54867139 :param q: accept数组,表示事件i占第i列矩形的面积的比例; :param J: alias数组,表示alias矩形的第i列中不是事件i的另一个事件的编号,也就是填充的那一列的序号; 生成一个随机数 kk in [0, K],另一个随机数 x in [0,1], 如果 x < accept[kk],表示接受事件kk,返回kk,否则拒绝事件kk,返回alias[kk] ''' K = len(J) kk = int(np.floor(np.random.rand()*K)) if np.random.rand() < q[kk]: return kk else: return J[kk]
文章出处登录后可见!
