Python-基于长短期记忆网络(LSTM)的SP500的股票价格预测股价预测 Python数据分析实战数据可视化时序数据预测变种RNN 股票预测

摘要

近些年，随着计算机技术的不断发展，神经网络在预测方面的应用愈加广泛，尤其是长短期记忆人工神经网络（Long Short-Term Memory，LSTM）在各领域、各学科都有应用。它是一种时间循环神经网络，是为了解决一般的RNN（循环神经网络）存在的长期依赖问题而专门设计出来的，非常适合处理长周期时间序列预测问题，并且预测速度快，准确度高。因此LSTM预测方法被广泛应用在天气预报、股票预测、行为预测等众多领域。基于这些优点，本文采用LSTM建立预测模型，根据美国标准普尔500股票指数的历史收盘价来预测未来收盘价的变化趋势。

关键词：LSTM长短期记忆人工神经网络，时间序列分析，股票预测

第一章前言

1.1 研究背景

股票市场具有高收益与高风险并存的特性，预测股市走势一直被普通股民和投资机构所关注。股票市场是一个很复杂的动态系统，受多方面因素的影响，例如国家金融政策的调整、公司内部结构的调整以及媒体舆论的渲染。针对股票预测，人们在长期实践和研究的基础上总结出一套股票预测方法，并进行了基本的统计分析，但这种传统的股票预测方法很难准确地揭示股票的变化规律。金融领域一直是机器学习算法应用较为活跃的领域，由于新的算法可能会给金融领域带来显著的经济利益，在人工智能和机器学习不断发展的背景下，金融领域的机器学习以及深度学习应用也得到了人们的关注。所以本文使用长短期记忆人工神经网络(LSTM)，一种在时间序列分析中有较好效果的深度学习模型，对美国标准普尔500股票指数的历史数据进行分析以及预测，试图探寻股票趋势之间的变化规律，并对股票市场的预测效果进行探索，帮助股民以及投资机构能更好地预测股市的走势。

1.2 研究现状

随着股票市场壮大，时间序列分析相应迎来崛起，时间序列的基本思想是利用序列变量与时间的关系建立统计模型来做预测。迄今为止，时间序列方法成果颇丰，相应诞生ARIMA差分整合移动自回归模型算法、滑动平均、指数平滑法、简单移动平均法、加权移动平均法、自回归滑动平均、广义自回归条件异方差以及蒙特卡洛模拟等时间序列模型。由于股票数据这种金融时间序列对象受到多种因素的影响，往往是非平稳的、非线性的以及高噪声的，不同于以往时间序列方法只涉及时间这个单方面影响因素，所以传统时间序列方法往往不适合股票数据，预测性能不够理想。而随着互联网与计算机技术的突破，数据存储技术的发展，迎来大数据时代，人们从电脑端和手机端不断地接触到大量的数据以及信息，对于庞大的数据，如何从中获得有用且人类想要的信息变为研究重点。由于股票市场的时效性，每天大批量数据的产生，迄今为止，股票市场已经累积了足量的历史数据，所以我们可以很好地利用以往的历史数据，通过分析这些数据，探寻其中的股票走势的规律，但是股票的价格受到大量因素的影响，这使得股价的预测不是那么容易，但是，随着机器学习技术的发展，使得从海量信息中挖掘出来对股票预测极其重要的信息有了一定的可能性，所以股票预测这项工作依然是具有极高的价值和意义的。

1.3 研究意义

在股票买卖过程中，如果建立了金融预测模型，我们将历史数据灌入，学习到参数，从而对未来的股票价格进行预测。假如模型的预测价格高于当天的收盘价格，即模型告诉我们未来股票价格可能出现上涨，则我们可以继续持仓这只股票以期获得后续更高的投资收益；另外，情况相反时，我们可以根据模型的建议采取相反的举措与动作。所以建立一个准确且高效的股票预测模型对于投资者更好的收益显得非常有意义。当然，找到这种股票价格上涨下跌趋势的规律对于国家宏观调控和企业的经营管理也是有很高的现实价值的。股票预测研究不仅仅聚焦在技术上，技术上的突破固然重要，但是在数据的处理以及特征工程上的精益求精上往往能给股票预测模型精度带来相当明显的提升。所以说股票预测这项工作依然是具有极高的价值和意义的，股票市场的价格波动研究不仅有重要的学术意义,而且有重要的实际意义。这能帮助我们更好的理解和把握股票市场的运行规律，以及探寻其对真实经济的影响机制与影响程度，能帮助我们在股票价格剧烈波动情况下选择并实施有效的货币政策，这有助于减轻和消除来自股票市场的不稳定因素，从而进一步提高各国宏观经济的运行质量。

第二章基本模型论述

2.1 LSTM模型的理论概述

长短期记忆神经网络(Long Short-Term Memory,LSTM)是一种时间递归神经网络，它在序列数据预测和建模方面表现出色。相对于传统的RNN模型，LSTM可以更好地处理长期依赖关系，并且不太容易出现梯度消失/爆炸的问题。LSTM模型的核心是记忆单元（memory cell），它允许模型选择性地接受、遗忘或输出信息。每个记忆单元都有三个门控，分别是输入门（input gate）、遗忘门（forget gate）和输出门（output gate）。这些门控允许模型拥有更加精细的控制能力，从而更好地捕获序列中的重要特征。具体而言，在每个时间步骤，LSTM模型会接受当前的输入和前一个时间步骤的隐藏状态作为输入，并计算出当前的输出和新的隐藏状态。

LSTM模型的训练过程采用反向传播算法，通过最小化损失函数来调整模型参数，从而使得模型能够更好地预测未知数据。在实际应用中，为了减少过拟合和提高模型性能，常常会结合dropout、正则化、批归一化等技术来进行模型优化。总之，LSTM模型在序列建模和预测任务中表现出色，能很好地解决自然语言处理、股票价格预测等问题，因此将利用LSTM模型应用到本文的股票预测中。

2.2 模型改进

LSTM模型有非常强大的功能，本文只是使用了相对简单的单步单特征的预测，更深入研究的话可以发现，LSTM还可以进行多步单特征，单步多特征，多步多特征等更强大的预测工作。除此之外，模型还可以从以下几个地方进行调整和改进，以获得更好的模型效果：

增加层数：增加模型的深度可以提高模型的表示能力和捕捉序列长时依赖关系的能力，同时也会增加模型的计算复杂度。通常可以使用堆叠多个LSTM层来增加模型的深度。
使用不同类型的门控机制：除了标准的forget gate、input gate和output gate之外，还可以尝试其他类型的门控机制，例如Peephole LSTM、Attention LSTM等。这些门控机制可以更好地适应特定的任务需求和数据特征。
添加注意力机制：引入注意力机制可以使LSTM模型更加关注重要的信息，从而提高模型的性能。
使用残差连接：在LSTM模型中添加残差连接可以帮助信息流更加顺畅地传播，避免信息在经过多个门控单元时被过度压缩或者丢失。
应用正则化技术：使用Dropout、L2正则化、Gradient Clipping等方法可以帮助防止过拟合和梯度消失/爆炸问题。
组合不同类型的RNN模型：可以将LSTM与GRU、RNN-T等不同类型的RNN模型组合，形成复合型的模型，以取长补短，进一步提高模型的性能。

第三章数据处理

3.1 数据读取与可视化展示

首先从包含 2010年1月1日至 2021年12月30日标准普尔 500 股票指数的开盘价、最高价、最低价、收盘价的美国标准普尔500指数历史数据.xls的excel文件根据时间拆分成2021年6月1日之前的训练数据TrainData.xls，2021年6月1日至12月30日的检验数据ValidateData.xls，以及2022年1月到3月30日的预测数据TestData.xls。数据格式大致如图所示：

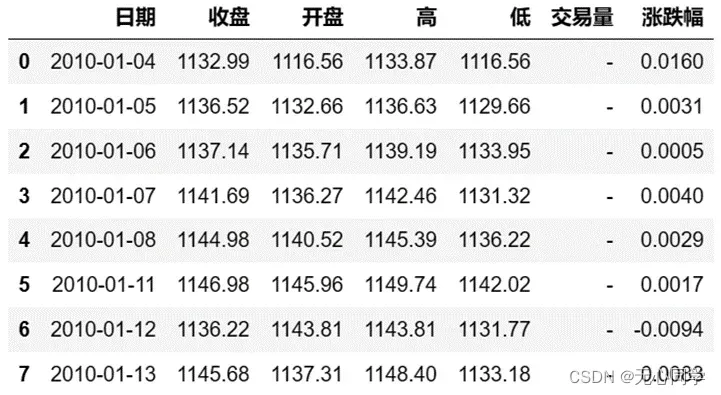
利用matplotlib绘图库，以日期作为横轴数据，收盘价作为纵轴数据对三个文件的整体数据做一个大致的可视化分析。训练数据，检验数据，预测数据的运行结果分别如下：

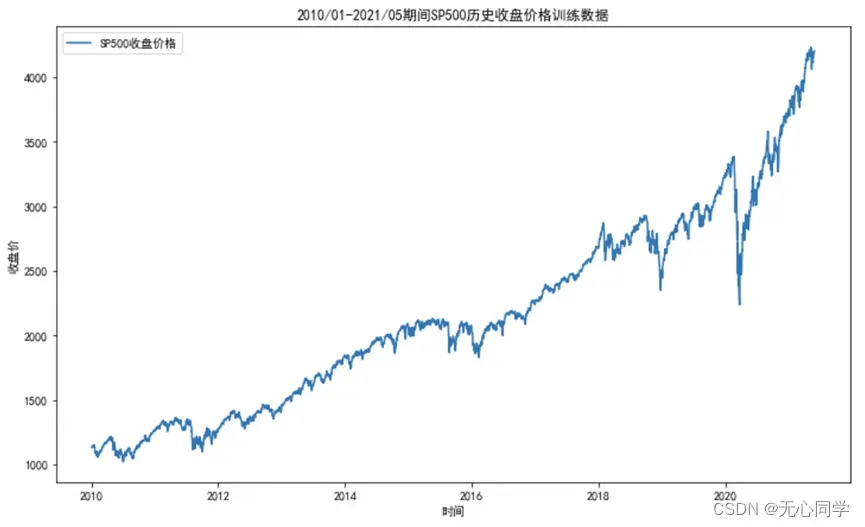
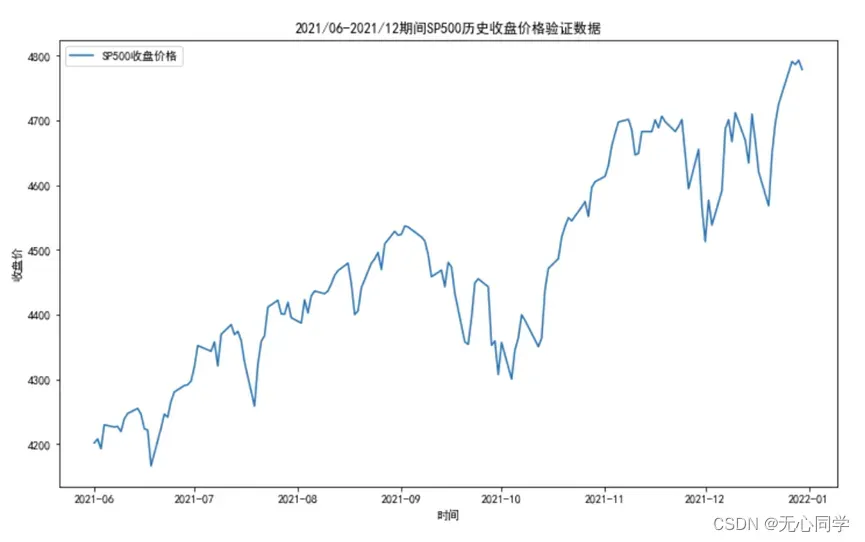
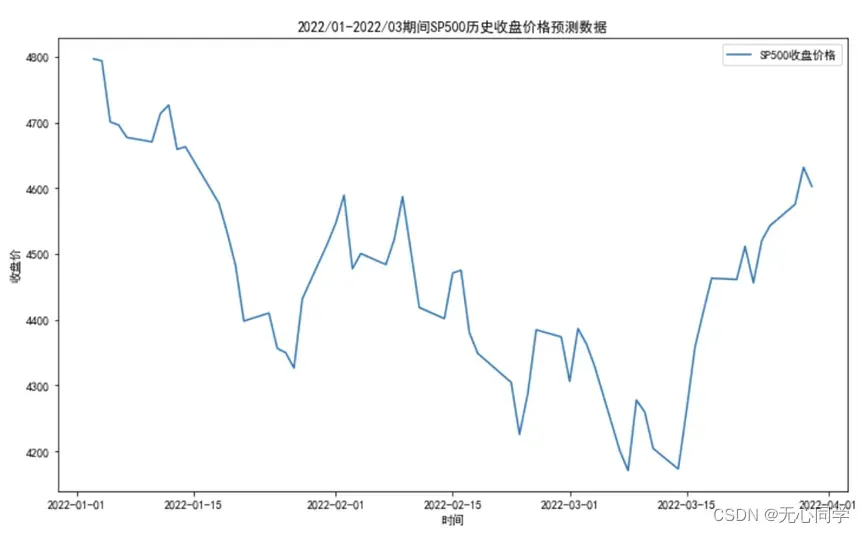
从运行结果来看，SP500的收盘价趋势除了中间几次断崖式暴跌之外，大致上是呈现上涨的趋势，具体放大细看的话不难发现，股票的收盘价整体上呈现一个波动的上涨趋势。

3.2 数据预处理

3.2.1 标准化数据

为了获得更好的拟合效果并防止训练发散，我们需要对数据进行标准化处理，也就是通过利用原数据减去训练数据的均值后再除以标准差得到标准化后的数据。数据标准化可以消除不同特征之间的量纲差异，使得特征之间具有可比性，从而提高模型的预测准确率。这里利用sklearn中的StandardScaler，对训练数据进行拟合，并对训练数据、验证数据以及预测数据进行转换。

3.2.2 准备预测变量以及响应变量

要预测序列在将来时间步的值，需要将响应变量指定为将值移位一个steptime时间步的训练序列，也就是取其[0:end-1]的数据作为预测的“输入数据”，[1:end]的数据作为预测的“标签数据”。也就是说，在输入序列的每个时间步，LSTM 网络都学习预测下一个时间步的值。预测变量是没有最终时间步的训练序列。

第四章数据分析

4.1 训练LSTM模型

通过Keras机器学习库提供的方法，搭建一个能用于时序序列分析的LSTM模型，模型的摘要图如图所示：

需要注意的是，LSTM模型的输入形状是一个三维的张量，也就是(batch_size, time_steps, input_dim)三个维度，分别对应的是批次大小，时间步长以及输入的特征维度，batch_size批次大小由后期训练时确定，因此设置成None；由于我们是测试单步预测的，因此时间步长设置成1；输入维度也仅仅是前一天的收盘价。因此该神经网络的输入就是（None, 1, 1）。为了挖掘到更深的特征，因此添加了一个有128个神经元的LSTM层以及一个64个神经元的LSTM层，并添加一个遗忘率为20%的Dropout遗忘层，表示将有20%的概率将神经元暂时从网络中丢弃，以此来防止过拟合的情况发生。最后再设置一个全连接层，最后以回归输出的形式将数据进行输出。

为了提高模型的训练效果，优化器将使用Adam算法，并且使用指数衰减的形式设置学习率，将Mean Squared Error均方误差设置为模型的损失函数，MSE的值越小，说明模型的性能越好，预测结果与真实值之间的差距越小。

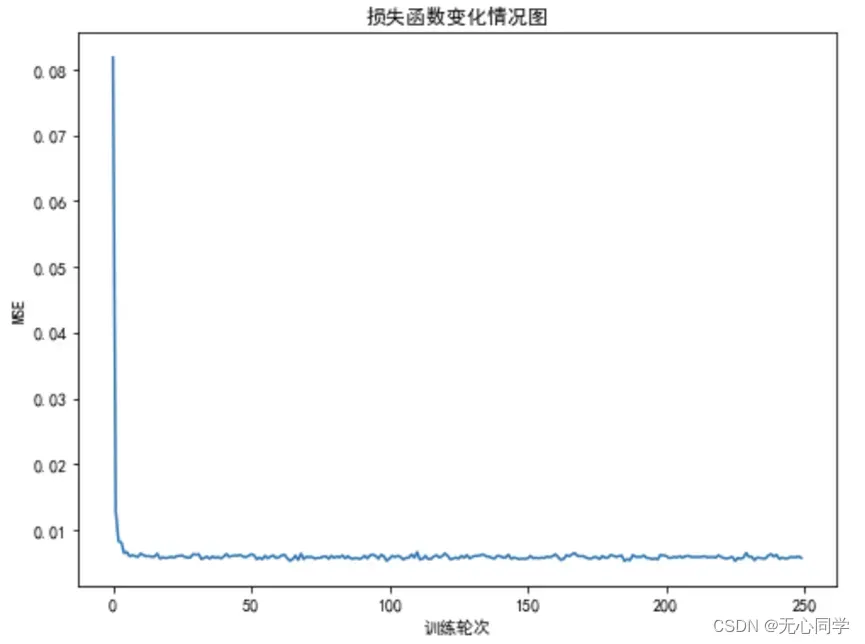
紧接着，我们调用模型的fit方法对训练数据进行拟合，设置批次大小为32，进行大概250轮的训练。训练的过程如图所示，可以看到，模型在训练了几个轮次之后，MSE均方误差在刚开始下降的比较快，到后来大概就在0.005左右不断地波动，可以从损失函数的变化情况看出模型的训练效果还是不错的。

4.2 模型效果检验

我们利用模型的predict方法，对检验数据进行预测。由于之前传入的数据是使用了标准化处理的，所以输出的预测值也是经过标准化后的数据，所以最终我们需要将预测的结果值反标准化，也就是利用inverse_transform方法，将预测结果转换为实际的预测值。

紧接着，我们需要根据去标准化的预测值去计算误差指标。对于 RMSE均方根误差，首先我们需要先获取到预测样本的真实值，然后对样本点的测量值和真实值求差，求平方后做平均运算，最后取根植，获取到RMSE均方根误差。对于MAE平均绝对误差，我们需要把预测值与真实值做差，然后取绝对值后做平均处理，最后获取到MAE平均绝对误差。对于MAPE平均绝对百分比误差，我们需要把预测值与真实值做差，结果除以真实值，取绝对值后做平均处理，最后获取到MAPE平均绝对百分比误差。检验数据的三个误差结果如图所示：

紧接着需要对检验数据的可视化展示，由于训练数据和检验数据是相连的，所以首先将训练数据和检验数据的预测值联合展示。运行结果如下：

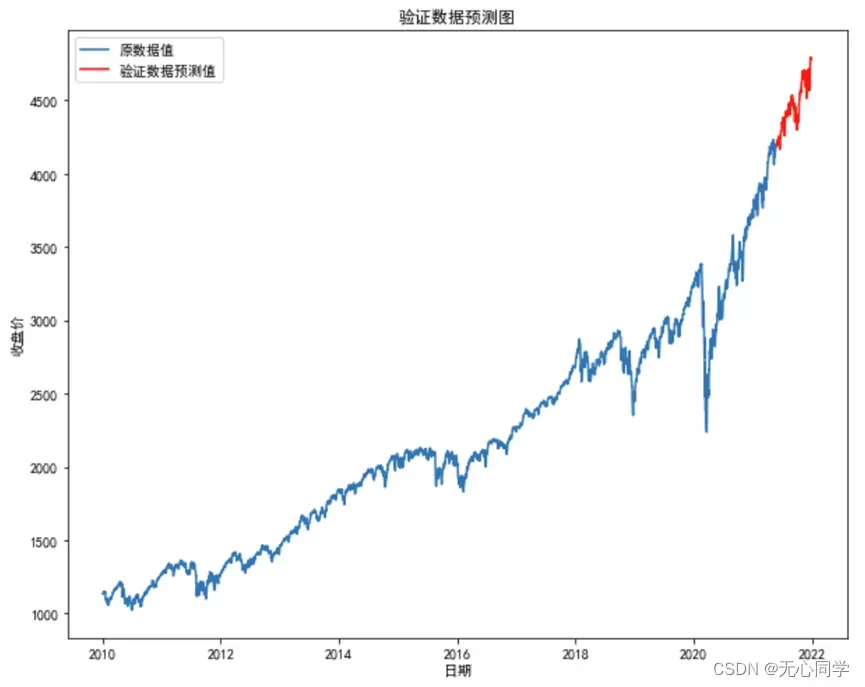
紧接着，将预测值与原数据放在一个折线图中进行比较，可以清楚地看到二者之间的趋势变化情况以及差距，运行结果如下图所示：

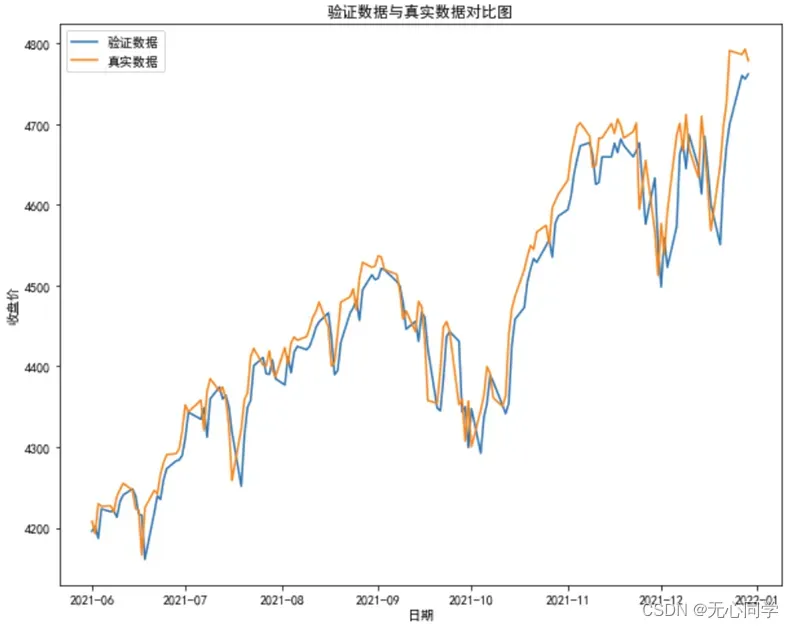
紧接着，再通过绘制出预测数据与原数据之间差值的棉棒图，来更清楚地看到预测的效果。棉棒图如图所示：

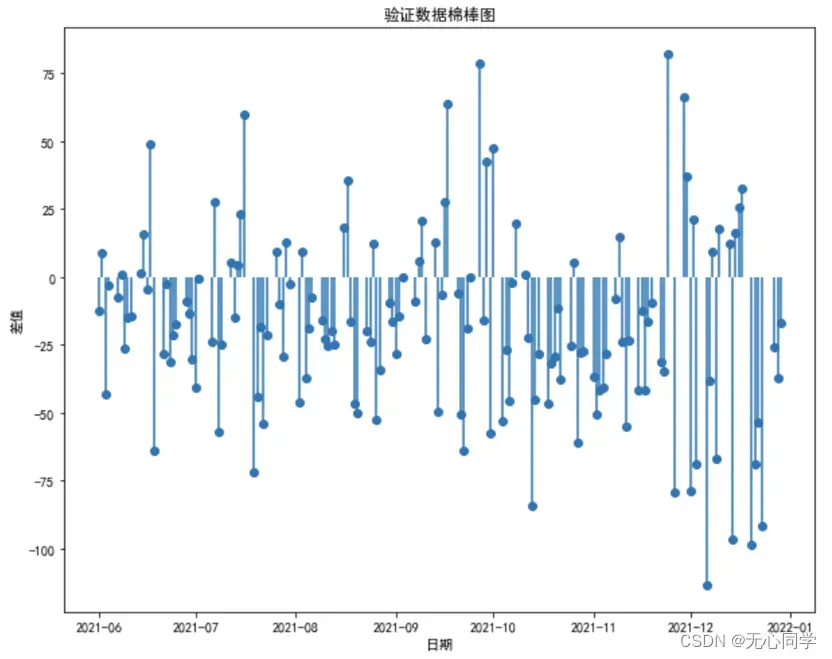
从如上的分析以及可视化结果来看，训练的模型对检验数据的拟合程度还是相当不错的，在大致的趋势上可以看到预测的效果与实际的效果是接近一致的，从误差棉棒图中也可以看出来误差的范围大概在(-110,80)之间，所以说整体的拟合效果是不错的。

4.3 预测将来的时间步

在将模型运用到验证数据进行预测之后，从三个评估指标可以看出，我们模型的训练效果是不错的，因此我们将利用训练好的模型，对未来的时间步进行预测。我们利用模型的predict方法，对预测数据进行预测。由于之前传入的数据是使用了标准化处理的，所以输出的预测值也是经过标准化后的数据，所以最终我们需要将预测的结果值反标准化，也就是利用inverse_transform方法，将预测结果转换为实际的预测值。

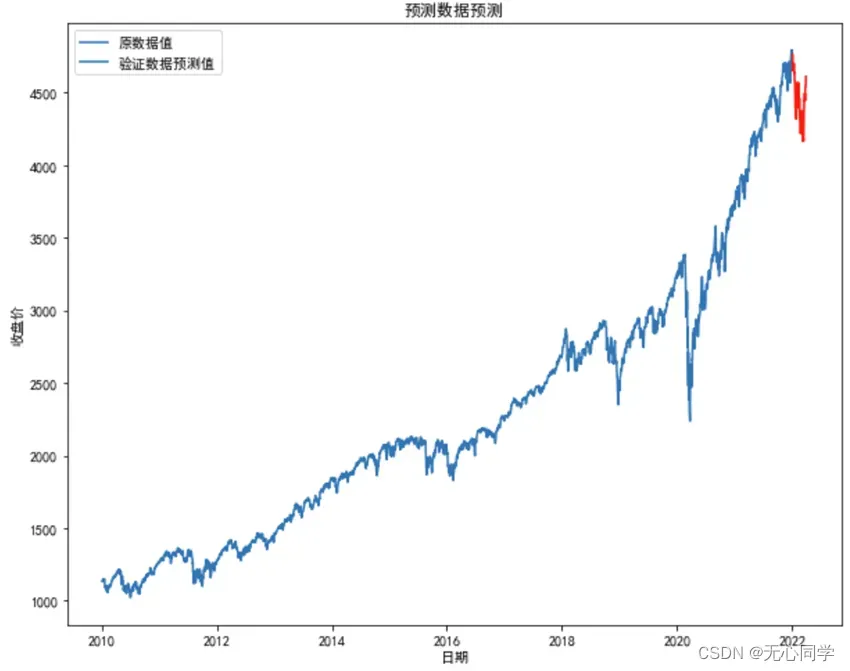
对预测数据进行可视化展示，首先需要将训练数据和检验数据拼接起来，绘制第一个图形，然后在此基础上，将预测的值用红色的折线绘制出来，并定义好横纵坐标，图例的显示设置。可视化结果如图所示：

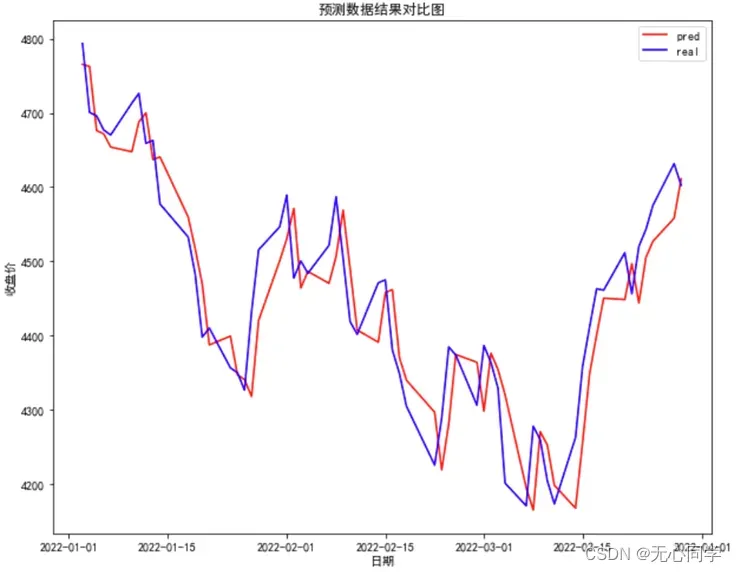
紧接着需要将预测数据单独拿出来与实际数据做一个对比，绘制出预测-实际的折线图，通过两条折现的变化趋势来确定模型的预测效果。可视化结果如图所示：

紧接着，再通过绘制出预测数据与原数据之间差值的棉棒图，来更清楚地看到预测的效果。棉棒图如图所示：

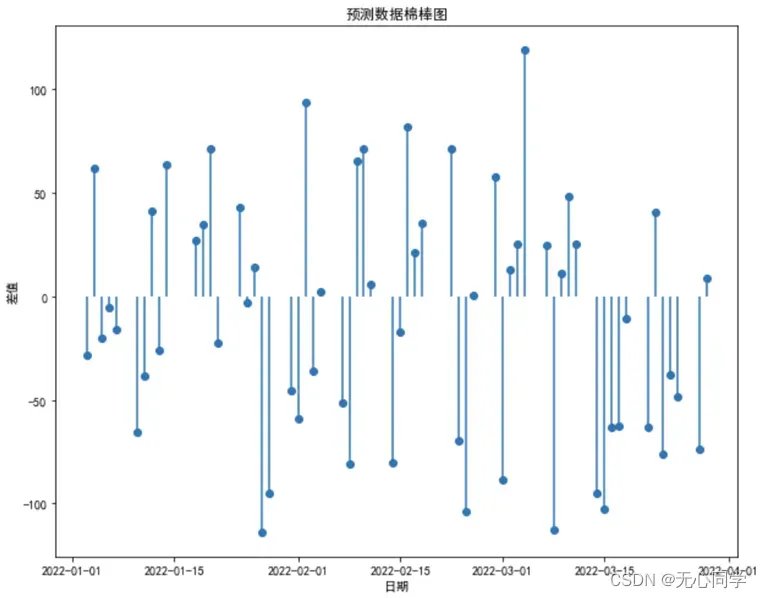
通过以上的预测分析可以看到，预测值与真实值之间存在一定的误差，误差范围大概在[-120,110]之间，但是大致趋势上还是吻合的。猜测误差较大的原因就是这个时间段内，股市的波动情况太大，导致根据前向的趋势预测后向的数据的精度有一定程度的下降，但是从整体上来看我们的预测效果还是不错的。

4.4 构建预测误差表

通过以上的预测结果（注：预测是利用2022/1/3-2022/3/29的数据去预测2022/1/4-2022/3/30的数据，因此第一天不算预测），有表展示：

时间真实值模型预测值预测误差
2022年01月03日 4796.56 4796.56 0
2022年01月04日 4793.54 4765.36084 -28.17916016
2022年01月05日 4700.58 4762.570313 61.9903125
2022年01月06日 4696.05 4676.085449 -19.96455078
2022年01月07日 4677.02 4671.842285 -5.177714844
2022年01月10日 4670.29 4653.98877 -16.30123047
2022年01月11日 4713.07 4647.664063 -65.4059375
2022年01月12日 4726.35 4687.770996 -38.57900391
2022年01月13日 4659.02 4700.173828 41.15382812
2022年01月14日 4662.85 4637.060547 -25.78945313
2022年01月18日 4577.34 4640.665527 63.32552734
2022年01月19日 4532.76 4559.755371 26.99537109
2022年01月20日 4482.73 4517.242188 34.5121875
2022年01月21日 4397.93 4469.27832 71.34832031
2022年01月24日 4410.13 4387.409668 -22.72033203
2022年01月25日 4356.45 4399.22998 42.77998047
2022年01月26日 4349.93 4347.12207 -2.807929688
2022年01月27日 4326.5 4340.775391 14.27539063
2022年01月28日 4431.85 4317.940918 -113.909082
2022年01月31日 4515.55 4420.239746 -95.31025391
2022年02月01日 4546.54 4500.772461 -45.76753906
2022年02月02日 4589.32 4530.406738 -58.91326172
2022年02月03日 4477.44 4571.14209 93.70208984
2022年02月04日 4500.54 4464.191406 -36.34859375
2022年02月07日 4483.87 4486.382813 2.5128125
2022年02月08日 4521.54 4470.374023 -51.16597656
2022年02月09日 4587.18 4506.508789 -80.67121094
2022年02月10日 4504.06 4569.109863 65.04986328
2022年02月11日 4418.64 4489.759277 71.11927734
2022年02月14日 4401.67 4407.466797 5.796796875
2022年02月15日 4471.07 4391.035156 -80.03484375
2022年02月16日 4475.01 4458.0625 -16.9475
2022年02月17日 4380.26 4461.854004 81.59400391
2022年02月18日 4348.87 4370.266113 21.39611328
2022年02月22日 4304.74 4339.743164 35.00316406
2022年02月23日 4225.5 4296.693359 71.19335938
2022年02月24日 4288.7 4219.016113 -69.68388672
2022年02月25日 4384.62 4281.007813 -103.6121875
2022年02月28日 4373.79 4374.499023 0.709023438
2022年03月01日 4306.26 4363.981934 57.72193359
2022年03月02日 4386.54 4298.178711 -88.36128906
2022年03月03日 4363.49 4376.362305 12.87230469
2022年03月04日 4328.87 4353.970215 25.10021484
2022年03月07日 4201.09 4320.252441 119.1624414
2022年03月08日 4170.62 4194.998047 24.37804688
2022年03月09日 4277.88 4164.962891 -112.9171094
2022年03月10日 4259.52 4270.415039 10.89503906
2022年03月11日 4204.31 4252.421387 48.11138672
2022年03月14日 4173.11 4198.168457 25.05845703
2022年03月15日 4262.45 4167.419434 -95.03056641
2022年03月16日 4357.95 4255.294922 -102.6550781
2022年03月17日 4411.67 4348.581055 -63.08894531
2022年03月18日 4463.09 4400.721191 -62.36880859
2022年03月21日 4461.18 4450.378906 -10.80109375
2022年03月22日 4511.61 4448.539063 -63.0709375
2022年03月23日 4456.23 4496.997559 40.76755859
2022年03月24日 4520.16 4443.769043 -76.39095703
2022年03月25日 4543.04 4505.1875 -37.8525
2022年03月28日 4575.52 4527.064941 -48.45505859
2022年03月29日 4631.6 4558.024414 -73.57558594
2022年03月30日 4602.45 4611.196777 8.746777344

第五章结论

这次金融大数据分析课程的股票预测作业，让我对深度学习与金融的结合有了全新的认识，在以往学习深度学习的过程，更多的是对现有代码的改进以及优化，实现的更多的是对图像处理的计算机视觉的学习。刚开始对时序数据的分析还是一个很懵懂的状态，然后通过查阅资料，知道了时序分析是以分析时间序列的发展过程、方向和趋势，预测将来时域可能达到的目标的方法。这运用了概率统计中时间序列分析原理和技术，利用时序系统的数据相关性，建立相应的数学模型，描述系统的时序状态，以达到预测未来的效果。而适合股票预测的方法有很多种，例如移动平均法、季节系数法、指数平滑法、自回归滑动平均模型(ARIMA)、随机森林等等，但是在查找资料的过程中发现，长短期记忆网络在时序数据的分析上有非常好的效果，传统的RNN在时序数据的分析中有较好的效果，之所以会有较好的预测效果是因为在 t时间点时会将 t-1时间点的隐节点作为当前时间点的输入，这样有效的原因是因为之前时间点的信息也用于计算当前时间点的内容，但是传统的RNN却存在长期依赖以及梯度消失或爆炸的问题，而LSTM的出现正是对RNN的一种补充，他能很好地利用”门机制”来控制特征的流通和损失，这使得它能解决RNN存在的问题并保留其优秀的时序分析的能力。经过先从python股票预测的LSTM的实现，再到matlab的编程实现，其中对LSTM的实现方法以及过程都经过了深入的理解，最终实现了基于LSTM模型的股票预测。

但是依旧存在一些的不足之处，比如在模型的优化上就无从下手，由于之前都是学习计算机视觉相关的图片识别类的深度学习课程，对于这类问题的提高精度和优化的方法更为擅长。因为是第一次接触时序数据的分析，所以在优化方面难免有些不足。除了影响股票价格的因素众多导致某一时间段的波动情况比较剧烈以外，模型本身还是有一些不足以及更大的优化空间的。所以在今后的学习中，我会努力学习并且深入研究深度学习中的神经网络在金融，大数据，统计分析等方面的运用，并且探寻能提高和优化算法的方法，以达到能更好、更高效地使用模型进行实际运用和操作的目的。

附录

1、训练参数设置代码

2、数据预览代码

3、训练数据，检验数据，预测数据标准化代码

4、定义LSTM回归网络与训练选项

5、计算RMSE，MAE，MAPE三大误差指标

6、可视化预测结果及对比代码

参考文献

[1] 张倩倩,林天华,祁旭阳,赵霞,基于机器学习的股票预测研究综述[J]. 河北省科学院学报,2020, 37(04):18-19.
[2] 隋金城.基于LSTM神经网络的股票预测研究[D].青岛科技大学,2020.
[3] 周阳.基于LSTM模型的上证综指价格预测研究[D].南京邮电大学,2019.

原文链接：https://blog.csdn.net/weixin_46990115/article/details/131216321

Python-基于长短期记忆网络(LSTM)的SP500的股票价格预测 股价预测 Python数据分析实战 数据可视化 时序数据预测 变种RNN 股票预测

摘要