遗传算法改进(IGA)+python代码实现
本文接我的上篇遗传算法python进阶理解+论文复现(纯干货,附前人总结引路)。首先声明,各位兄弟姐妹们一定要在对遗传算法有一定了解的基础上,再来看这篇。
废话不多讲,本文根据现有的文献对遗传算法进行改进,但文献中给出的只是文字逻辑和一些伪代码,而本文会用python对它复现,并以用例来测试。
IGA由易到难,我依次来介绍对变异概率的改进、交叉概率的改进和适应度函数的改进。
注:本文的测试用例都是来自与我上篇文章遗传算法python进阶理解+论文复现(纯干货,附前人总结引路)中复现的论文,各种参数的含义和设置在上篇中都有详细地介绍。
一、变异概率的改进
(1)单点变异
首先我们回忆下最常用的基本位变异算子:个体的DNA是否发生变异以及发生变异的位置都是随机产生的:
def mutation(child, MUTATION_RATE=0.005):
if np.random.rand() < MUTATION_RATE: # 以MUTATION_RATE的概率进行变异
mutate_point = np.random.randint(0, DNA_SIZE * 4) # 随机产生一个实数,代表要变异基因的位置
child[mutate_point] = child[mutate_point] ^ 1
上面这段很好理解,很多文章里也有对它的讲解。接着我们看参考文献11中的对交叉概率的设计思路,本质上是一种多点变异:
(2)多点变异
“单性繁殖”的具体过程如下:随机产生变异(所谓变异是将二进制串的某些位进行翻转,即 0 变成 1 或1 变成 0)的参考位 N(1≤N≤80);随机产生变异的参考起始位置 P(1≤P≤79);确定变异的始末位置 a 和 b(显然 a≤b),若 N≥P,则 a=0,b=P-1;若 N<P,则 a=N, b=P。这样,在表征最优个体的二进制串中有 k 位(k=b-a+1)需要变异。新种群包含的个体数目与上一代种群相同。
上面这段话把它的逻辑写下来实际上就是下面这几步:

因此不同于上面的单点变异,这种方法规定了一个区间[a,b],在这个小区间内的所有点都发生变异,一共有k个点(k=b-a+1)进行了变异。程序写出来是:
# 参考文献1中的多点变异
def mutation2(child, MUTATION_RATE=0.005):
N = np.random.randint(1, 81) # 1≤N≤80
P = np.random.randint(1, 80) # 1≤P≤79
a = 0
b = 0
if N >= P:
a = 0
b = P - 1
else:
a = N
b = P
for i in range(a, b + 1):
child[i] = child[i] ^ 1
(3)选择性的突变概率
该方法来源于参考文献22,首先来看文章中的方法描述:

上面是改进后的突变算法的伪代码。首先简单突变设定了一个相对较大的突变率(0.025),当产生的随机数小于突变率时,就会使进入的儿童染色体上的任何一个基因发生突变。在本文中,我们改进了该算法,通过设置一个小的突变率,然后选择性地突变进入的儿童染色体上的每个基因。也就是说,当生成的随机数小于突变率,基因突变。当遍历基因位置大于染色体长度的一半,突变率设置为原来的两倍(下一半的基因对结果的影响相对较小)。这就保证了基因的前半部分和基因的后半部分分别具有相同的突变机会,并且可以同时发生突变。
用程序写出来即为:
def mutation_develop(child, MUTATION_RATE=0.005):
# 选择性地突变概率,即当遍历的基因位置大于染色体长度的一半时,设置突变率为原来的a两倍
mutate_point = np.random.randint(0, DNA_SIZE * 4) #随机产生变异基因的位置
if mutate_point >= DNA_SIZE / 2:
MUTATION_RATE = MUTATION_RATE * 2
if np.random.rand() < MUTATION_RATE:
child[mutate_point] = child[mutate_point] ^ 1
编好程序后,我们在代码的相应位置修改为自己想要的变异概率算子,就能跑出来了。
二、交叉概率的改进
第二个是交叉概率的改进,该方法仍来源于参考文献22,首先看方法描述:
!](https://img-blog.csdnimg.cn/53a8c79dcfe748778954c6b541249be4.png)

上面是改进的交叉算法的Python伪代码。
普通的交叉算法是在亲本染色体长度范围内生成一个随机数,然后截取父亲染色体的前半部分和母亲染色体的后半部分,根据生成的随机数对孩子进行杂交。
本文改进了该算法,试图逐个杂交亲本染色体长度范围内的基因,计算适应度,并筛选出适应度最高的儿童个体。实验数据表明,这种改进可以减少迭代次数,加快适应度的收敛速度。
上面这几段是文章对于改进后交叉算法的解释。我们通过阅读伪代码就可以知道,它需要输入两个基因,分别是1个父体基因和1个母体基因,一个计算单个个体适应度的函数,最后能够输出当代中最优的1个个体基因。
因此,为了不失普遍性,在编程时,首先在所有个体中随机产生一个父体和母体。而之前用的适应度函数是针对当代个体的矩阵(维度是15080)来进行的,是二维的,而这种方法是对单个个体(维度是180)计算适应度,因此在这里不能直接调用,需要将其调整为一维。
为了方便看结果,最后我输出两个值:最优个体和对应的最优适应度。
计算适应度需要将基因的二进制解码为十进制来计算,因此我们首先调整解码的程序:
def translate_singleDNA(pop):
# 这里表示对单个个体的DNA进行解码,维度是1维
p1_pop = pop[:20]
p2_pop = pop[20:40]
q1_pop = pop[40:60]
q2_pop = pop[60:]
# pop:(POP_SIZE,DNA_SIZE)*(DNA_SIZE,1) --> (POP_SIZE,1) 进行解码的过程
p1 = p1_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (p1_BOUND[1] - p1_BOUND[0]) + p1_BOUND[
0]
p2 = p2_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (p2_BOUND[1] - p2_BOUND[0]) + p2_BOUND[
0]
q1 = q1_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (q1_BOUND[1] - q1_BOUND[0]) + q1_BOUND[
0]
q2 = q2_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (q2_BOUND[1] - q2_BOUND[0]) + q2_BOUND[
0]
return p1, p2, q1, q2
def calcu_fitness(singlepop):
p1, p2, q1, q2 = translate_singleDNA(singlepop)
pred = F(p1, p2, q1, q2)
# 求最小值问题,目标函数值越小,适应度越高
# 这里借用sigmoid函数,目标函数值越小,适应度越高
return (1 + np.exp(pred)) ** (-1)
def crossover_develop(pop):
mother = pop[np.random.randint(POP_SIZE)]
father = pop[np.random.randint(POP_SIZE)]
best_child = np.zeros(father.size)
best_fitness = 0
for i in range(len(father)):
current_child = np.append(father[0:i], mother[i:])
# np.append()用于合并两个数组
current_fitness = calcu_fitness(current_child)
if current_fitness > best_fitness:
best_fitness = current_fitness
best_fitness = np.log(best_fitness ** (-1) - 1)
# 取反函数,得到原本的适应度
best_child = current_child
return best_child, best_fitness
因为是随机算法,程序每次跑的结果都不一样,截取一次跑的结果:
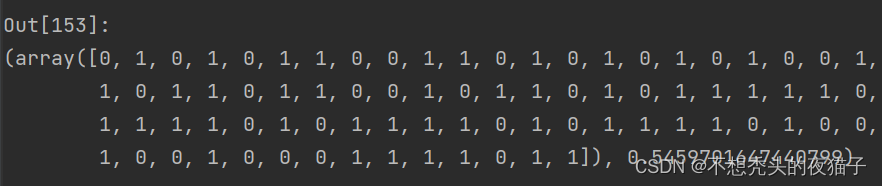
将上面的best_child解码为十进制translate_singleDNA(best_child) ,四个参数值p1,p2,q1,q2分别为:
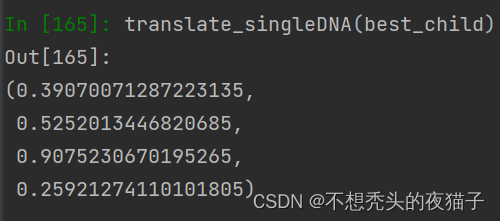
这种方法本质上是穷举交叉点,找到在给定父体和母体基因下的1个最优的个体基因。
需要注意的是:通过该方法我们只能得到一个个体,如果要得到当代的个体种群,可以考虑写一个for循环,不断调用该函数,直到生成指定的种群数量。
三、适应度函数的改进
第三点是对适应度函数的改进。其实在第二个改进中计算适应度函数已经提到过,这里会用到重要的sigmoid函数(1 + np.exp(pred)) ** (-1) 。
该方法的设计思路来自于参考文献33。
(1)sigmoid函数
由于适应度函数设计时通常要求其值域在[0,1]之间,考虑 logistic曲线:的值域恰好在(0,1)之间,小于0时值域在(0.5,1)之间,大于等于0时值域在(0,0.5]之间,其取值范围在[-10,10]之间的函数图象如图所示:
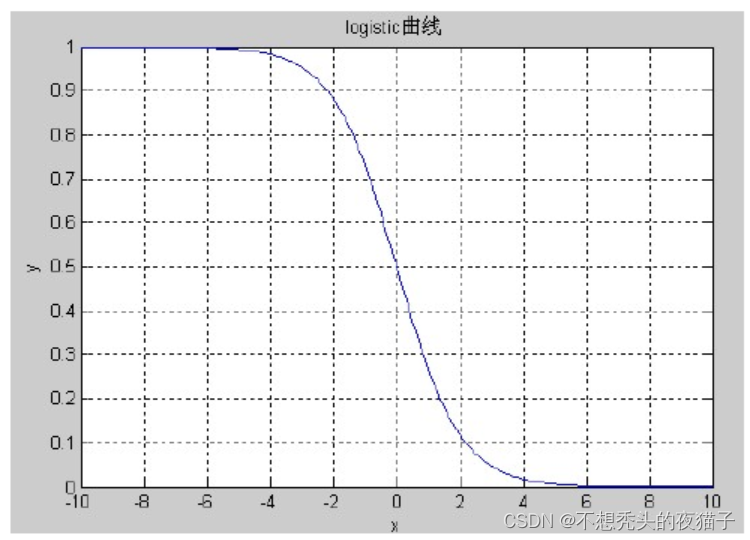
(2)适应度函数设计思路
适应度函数的设计,要求在进化初期控制适应度较高个体的适应度值,减小其与其它适应度值的差异,限制它的复制数量;
进化后期,要防止因平均适应度值和最佳适应度值相近而导致的竞争力不强的问题的产生,故要使个体的适应度值与最佳个体适应度值的差异增大,使种群的竞争力增强。
因此当种群中个体适应度值与平均适应度值相接近时,说明种群中的个体比较相似,那么就需要增大种群中个体适应度值之间的差异,使得种群中个体的竞争力加强。但是logistic曲线在[-10,10]之外,函数值接近于1或者0,若有较多个体的适应度值接近于1或者0,那么个体适应度值则很接近。这将导致竞争力不强。
因此该方法会保留前30%的优良模式不参与交叉和变异。若在进化初期种群中有较多个体适应度值接近于1,这些个体将迅速占领种群。一般情况下,这些个体不会是全局最优解,这种情况将会造成早熟现象的产生。为防止这种现象的发生,在适应度函数设计时加入适应度值接近1或者0的个体数目的判断。
因此该方法设计的适应度函数为:
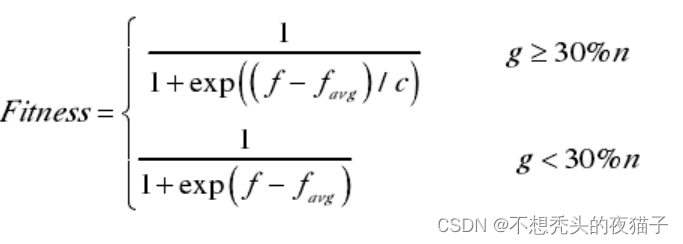
其中,f为原适应度,如果问题本身是求最小值问题,f可取目标函数,假如问题本身是求最大值,那么需要将问题转化为求极小值的问题。
为当代种群的适应度的平均值。将每个个体的
值与
作差,g表示在(-10,10)以外的个体的数目;c表示
值与
的差的绝对值的最大值的数量级。
的求法,
avg_fitness即为所求:
def origin_fitness(pop): # 原适应度函数
p1, p2, q1, q2 = translateDNA(pop)
# 这里的pi、qi都是长度为150的向量
pred = F(p1, p2, q1, q2)
return -(pred - np.max(pred)) + 1e-3
# 当代个体适应度的平均值
avg_fitness = np.mean(origin_fitness(pop))
原适应度函数复合sigmoid函数后,即get_fitness1(pop):
def get_fitness1(pop):
return (1 + np.exp(origin_fitness(pop))) ** (-1)
当g>=30%时,即
get_fitness2(pop):
# 求每个个体适应度-当代个体适应度的最大值的绝对值
def get_fitness2(pop): # g>=0.3*n时
b = [np.abs(i - np.max(origin_fitness(pop))) for i in origin_fitness(pop)]
c = np.max(b)
return (1 + np.exp((origin_fitness(pop) - avg_fitness) / c)) ** (-1)
当g<30%时,即
get_fitness3(pop):
# g<0.3*n时
def get_fitness3(pop):
return (1 + np.exp(origin_fitness(pop) - avg_fitness)) ** (-1)
上面是分析这种做法的理论依据,但是转化为程序实现,仍然有几个问题:
-
当参数不只一个的时候,判断x是否落在(-10,10)以外不好操作,如本题的参数个数为4个。而它这个做法本质上是要找接近0或者1的极端值,因此我们可以将对x的判断转化到对y的判断上来。即对每组解(p1,p2,q1,q2)计算它的适应度函数,当适应度值满足一定条件就计数加1,直到计数超过当代个体数量的30%,代入相应的适应度表达式。
-
在进化早期,要防止早熟发生;在进化后期,要使得个体的竞争力增强。但是何时进行“适应度接近极端值”的判断,文章并未指出。但我们能预料的是,肯定是在进化一些代数后,来考察当代中有多少个体的适应度接近0或者1。因此为了程序可行性,我在进化代数进行到一半时,进行上式的条件判断。
将对x落在[-10,10]区域外的判断转换到对y的值域上来:
def expfun(x):
return (1 + np.exp(x)) ** (-1)
upper = expfun(-10) # 0.9999546021312976
lower = expfun(10) # 4.5397868702434395e-05
因此,第三部分对适应度函数的改进中,整个程序大概可以分成两部分,第一部分是在前半程的进化中,我们利用get_fitness1(pop)函数来计算个体的适应度;
因为已经经常一段时间的进化,因此可能会有少数优良个体的适应度接近于0或者1,然后我们再利用上式进行判断,当这种优良个体的数量大于等于种群数量(即POP_SIZE)的30%时,我们代入get_fitness2(pop)计算个体适应度,否则代入get_fitness3(pop)函数。
编程如下:
# 生成初试种群
pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE * 4))
# 在前半程的进化中
for _ in range(int(N_GENERATIONS / 2)):
pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE)) # 交叉和变异
fitness = get_fitness1(pop)
pop = select(pop, fitness) # 选择
# 下面进行上式的条件判断,来分别代入get_fitness2(pop)或者get_fitness3(pop)
# 在后半程的进化中
for _ in range(int(N_GENERATIONS / 2), N_GENERATIONS):
i = 0
pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE))
for i in fitness:
if i >= upper or i <= lower:
i += 1
if i >= 0.3 * POP_SIZE:
fitness = get_fitness2(pop)
else:
fitness = get_fitness3(pop)
pop = select(pop, fitness)
print_info(pop)
最后跑出的结果:

注:上述我在编程中还遇到了一个问题,就是找出前30%的优良个体,并且保证它们不参与后面的交叉和变异。但是大家想一想,就知道编起来很麻烦。
因为这前30%的种子不好一一对应,就算能够对应,也要修改选择函数和交叉变异函数中的相关参数。有兴趣的同学可以再研究研究,跑出来的话也请告诉我!
下面附上完整代码:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
import warnings
warnings.filterwarnings('ignore')
DNA_SIZE = 20 # DNA长度(二进制编码长度)
POP_SIZE = 150 # 初始种群数量
CROSSOVER_RATE = 0.95 # 交叉率
MUTATION_RATE = 0.005 # 变异率 将0.005改为0.01
N_GENERATIONS = 1000 # 进化代数 进化代数在 800—1200 之间比较适合,本文选取进化1000代
p1_BOUND = [0, 1] # 确定参数的范围
p2_BOUND = [0, 1]
q1_BOUND = [0, 1]
q2_BOUND = [0, 1]
dic_liver = {0.167: 0.681, 0.5: 0.436, 1: 0.709, 2: 0.263, 6: 0.12} # 键表示时间(h),值表示肝内的浓度
dic_lung = {0.167: 1.069, 0.5: 0.689, 1: 0.666, 2: 0.342, 6: 0.162} # 表示肺内的浓度
dic_stomach = {0.167: 4.827, 0.5: 3.866, 1: 1.67, 2: 1.638, 6: 0.798} # 表示胃内的浓度
def F(p1, p2, q1, q2): # 设计适应度函数 法一
fun = 0
for key, value in dic_liver.items():
fun = ((p1 * np.exp(-q1 * key) + p2 * np.exp(-q2 * key)) - value) ** 2 + fun
return 1 / (1 + np.exp(-fun))
# return fun
def F2(p1, p2, q1, q2): # 设计适应度函数 法二
result = [((p1 * np.exp(-q1 * i) + p2 * np.exp(-q2 * i)) - j) ** 2 for i, j in zip(l1, l2)]
total = 0
for i in range(len(result)):
total = total + result[i]
return total
# 求最小值 函数值越小的可能解对应的适应度应该越大
def get_fitness(pop):
p1, p2, q1, q2 = translateDNA(pop)
pred = F(p1, p2, q1, q2)
return -(pred - np.max(pred)) + 1e-3
def translateDNA(pop): # pop表示种群矩阵
p1_pop = pop[:, :20]
p2_pop = pop[:, 20:40]
q1_pop = pop[:, 40:60]
q2_pop = pop[:, 60:]
p1 = p1_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (p1_BOUND[1] - p1_BOUND[0]) + p1_BOUND[
0]
p2 = p2_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (p2_BOUND[1] - p2_BOUND[0]) + p2_BOUND[
0]
q1 = q1_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (q1_BOUND[1] - q1_BOUND[0]) + q1_BOUND[
0]
q2 = q2_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (q2_BOUND[1] - q2_BOUND[0]) + q2_BOUND[
0]
return p1, p2, q1, q2
def crossover_and_mutation(pop, CROSSOVER_RATE=0.95): # 单点交叉
new_pop = []
for father in pop: # 遍历种群中的每一个个体,将该个体作为父亲
child = father
if np.random.rand() < CROSSOVER_RATE: # 产生子代时不是必然发生交叉,而是以一定的概率发生交叉
mother = pop[np.random.randint(POP_SIZE)] # 再种群中选择另一个个体,并将该个体作为母亲
cross_points = np.random.randint(low=0, high=DNA_SIZE * 4) # 随机产生交叉的点
child[cross_points:] = mother[cross_points:] # 孩子得到位于交叉点后的母亲的基因
mutation(child) # 每个后代有一定的机率发生变异
new_pop.append(child)
return new_pop
# 基本位变异算子
def mutation(child, MUTATION_RATE=0.005):
if np.random.rand() < MUTATION_RATE: # 以MUTATION_RATE的概率进行变异
mutate_point = np.random.randint(0, DNA_SIZE * 4) # 随机产生一个实数,代表要变异基因的位置
child[mutate_point] = child[mutate_point] ^ 1
def select(pop, fitness):
# 描述了从np.arange(POP_SIZE)里选择每一个元素的概率,概率越高约有可能被选中,最后返回被选中的个体即可
idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
p=(fitness) / (fitness.sum()))
return pop[idx]
def print_info(pop):
fitness = get_fitness(pop)
min_fitness_index = np.argmin(fitness) # 表示为array的最大值/最小值对应的索引
print("min_fitness:", fitness[min_fitness_index])
p1, p2, q1, q2 = translateDNA(pop)
print("最优的基因型:", pop[min_fitness_index])
print("(p1, p2, q1, q2):",
(p1[min_fitness_index], p2[min_fitness_index], q1[min_fitness_index], q2[min_fitness_index]))
# --2023.1.3 遗传算法的改进,以我复现的论文为例-----------------------------------
# ---NO.1 对适应度函数的改进---------------------------------------------------
# 第一步:将适应度函数代入sigmoid函数中,y=1/(1+np.exp(x)),此时适应度函数的范围调整至(0,1)之间
# 第二步:当进化代数进行到一半时(我自己定的),对它进行条件判断
# 第三步:这里对x范围的判断实际上是为了确定极端值的数量,所以可以将它转换为对y范围的判断
# 第四步:更新每次循环后的适应度函数
def origin_fitness(pop): # 原适应度函数
p1, p2, q1, q2 = translateDNA(pop)
pred = F(p1, p2, q1, q2)
return -(pred - np.max(pred)) + 1e-3
avg_fitness = np.mean(origin_fitness(pop)) # 当代个体适应度的平均值
def get_fitness1(pop): # 代入sigmoid函数后
return (1 + np.exp(origin_fitness(pop))) ** (-1)
def get_fitness2(pop): # g>=0.3*n时
b = [np.abs(i - np.max(origin_fitness(pop))) for i in origin_fitness(pop)]
c = np.max(b)
return (1 + np.exp((origin_fitness(pop) - avg_fitness) / c)) ** (-1)
def get_fitness3(pop): # g<0.3*n时
return (1 + np.exp(origin_fitness(pop) - avg_fitness)) ** (-1)
# 将x在(-10,10)的范围的判断转换到对y的判断上来
def expfun(x):
return (1 + np.exp(x)) ** (-1)
upper = expfun(-10) # 0.9999546021312976
lower = expfun(10) # 4.5397868702434395e-05
if __name__ == "__main__":
pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE * 4))
for _ in range(int(N_GENERATIONS / 2)):
pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE)) # 进行交叉和变异
fitness = get_fitness1(pop)
pop = select(pop, fitness) # 选择
# 下面进行件判断,来分别代入get_fitness2(pop)或者get_fitness3(pop)
for _ in range(int(N_GENERATIONS / 2), N_GENERATIONS):
i = 0
pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE))
for i in fitness:
if i >= upper or i <= lower:
i += 1
if i >= 0.3 * POP_SIZE:
fitness = get_fitness2(pop)
else:
fitness = get_fitness3(pop)
pop = select(pop, fitness)
print_info(pop)
# ---NO.2 对变异概率的改进--------------------------------------
def mutation_develop(child, MUTATION_RATE=0.005): # 改进的变异算法,即当遍历的基因位置大于染色体长度的一半时,设置突变率为原来的a两倍
mutate_point = np.random.randint(0, DNA_SIZE * 4)
if mutate_point >= DNA_SIZE / 2:
MUTATION_RATE = MUTATION_RATE * 2
if np.random.rand() < MUTATION_RATE:
child[mutate_point] = child[mutate_point] ^ 1
# ----本文给出的变异概率设计思路--------------
# 本文的多点交叉变异
def mutation(child, MUTATION_RATE=0.005):
N = np.random.randint(1, 81) # 1≤N≤80
P = np.random.randint(1, 80) # 1≤P≤79
a = 0
b = 0
if N >= P:
a = 0
b = P - 1
else:
a = N
b = P
for i in range(a, b + 1):
child[i] = child[i] ^ 1
# --NO.3 交叉概率的改进--------
# 注:这种改进利用穷举交叉点的方法,返回的仅是单个最优个体,而不是像上面的方法返回的是个体矩阵
def translate_singleDNA(pop):
# 这里表示对单个个体的DNA进行解码,维度是1维
p1_pop = pop[:20]
p2_pop = pop[20:40]
q1_pop = pop[40:60]
q2_pop = pop[60:]
p1 = p1_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (p1_BOUND[1] - p1_BOUND[0]) + p1_BOUND[
0]
p2 = p2_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (p2_BOUND[1] - p2_BOUND[0]) + p2_BOUND[
0]
q1 = q1_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (q1_BOUND[1] - q1_BOUND[0]) + q1_BOUND[
0]
q2 = q2_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (q2_BOUND[1] - q2_BOUND[0]) + q2_BOUND[
0]
return p1, p2, q1, q2
def calcu_fitness(singlepop):
p1, p2, q1, q2 = translate_singleDNA(singlepop)
pred = F(p1, p2, q1, q2)
# 求最小值问题,目标函数值越小,适应度越高
return (1 + np.exp(pred)) ** (-1)
def crossover_develop(pop):
mother = pop[np.random.randint(POP_SIZE)]
father = pop[np.random.randint(POP_SIZE)]
best_child = np.zeros(father.size)
best_fitness = 0
for i in range(len(father)):
current_child = np.append(father[0:i], mother[i:]) # np.append()用于合并两个数组
current_fitness = calcu_fitness(current_child)
if current_fitness > best_fitness:
best_fitness = current_fitness
# 取反函数,得到原本的适应度
best_fitness = np.log(best_fitness ** (-1) - 1)
best_child = current_child
return best_child, best_fitness
if __name__ == "__main__":
crossover_develop(pop)
以上文献的搜集理解和代码的复现花了我大量的时间和心血,就像亲儿子一样。
所以转载请注明出处,希望对各位兄弟姐妹们有所帮助!
孙亮,李君利,程建平.一种基于遗传算法和高斯-牛顿法的合成算法在放射性药物生物动力学数据分析中的应用[J].核技术,2006(12):927-931. ↩︎
Gao Q , Qi K , Lei Y , et al. An Improved Genetic Algorithm and Its Application in Artificial Neural Network Training[C]// 2005 5th International Conference on Information Communications & Signal Processing. 0. ↩︎ ↩︎
李延梅. 一种改进的遗传算法及应用[D].华南理工大学,2012. ↩︎
文章出处登录后可见!
