考研408每周一题（2019 41）

2019年(单链表）

41.(13分)设线性表L=(a1,a2,a3,…,a(n-2),a(n-1),an)采用带头结点的单链表保存，链表中的结点定义如下：

typedef struct node {
    int data;
    struct node *next;
} NODE;

请设计一个空间复杂度为O(1)且时间上尽可能高效的算法，重新排列L中的各个结点，得到线性表L’=(a1,an,a2,a(n-1),a3,a(n-2),…)。要求：

(1)给出算法的基本设计思想

我们将n用数字代入进去，比如n=7，那么L也就是如下图所示

重新排列组合之后的L’

很容易就能发现一下规律，将链表L断开（断链），将链表尾进行反转(逆置)，最后重新组合成一条新的链表。这个我们用三个函数(list_spilt、list_reverse、list_merge)来对链表L进行操作。

(2)根据设计思想，采用C或C++语言描述算法，关键之处给出注释

环境：Visual Studio 2022

语言：C++

代码如下图所示：

链表断链

//链表断链
void list_spilt(LinkList L, LinkList& L2) {
	LinkList q, p;
	L2 = (LinkList)malloc(sizeof(Lnode));
	//将p和q进行初始化
	p = q = L->next;
	//需要对当前指针进行判断
	//如果当前指针为空的情况
	//开始遍历
	while (p) {
		p = p->next;
		//防止链表只有一个结点的情况
		if (p == NULL) {
			break;
		}
		p = p->next;
		//为了偶数个的情况进行判断
		if (p == NULL) {
			break;
		}
		q = q->next;
	}
	//L2的相关操作
	//将L2的链表头节点指向当前链表的中间结点q
	L2->next = q->next;
	//将中间结点q的next置为NULL(即为L链表的断链)
	q->next = NULL;
}

顾名思义就是将链表一分为二，这里我们用快慢指针，快指针p走两步，慢指针q走一步，保证快指针p始终走的比慢指针q多一个单位，因此 ,循环的条件就是快指针p不为空，考虑到p为空的情况，循环即结束。

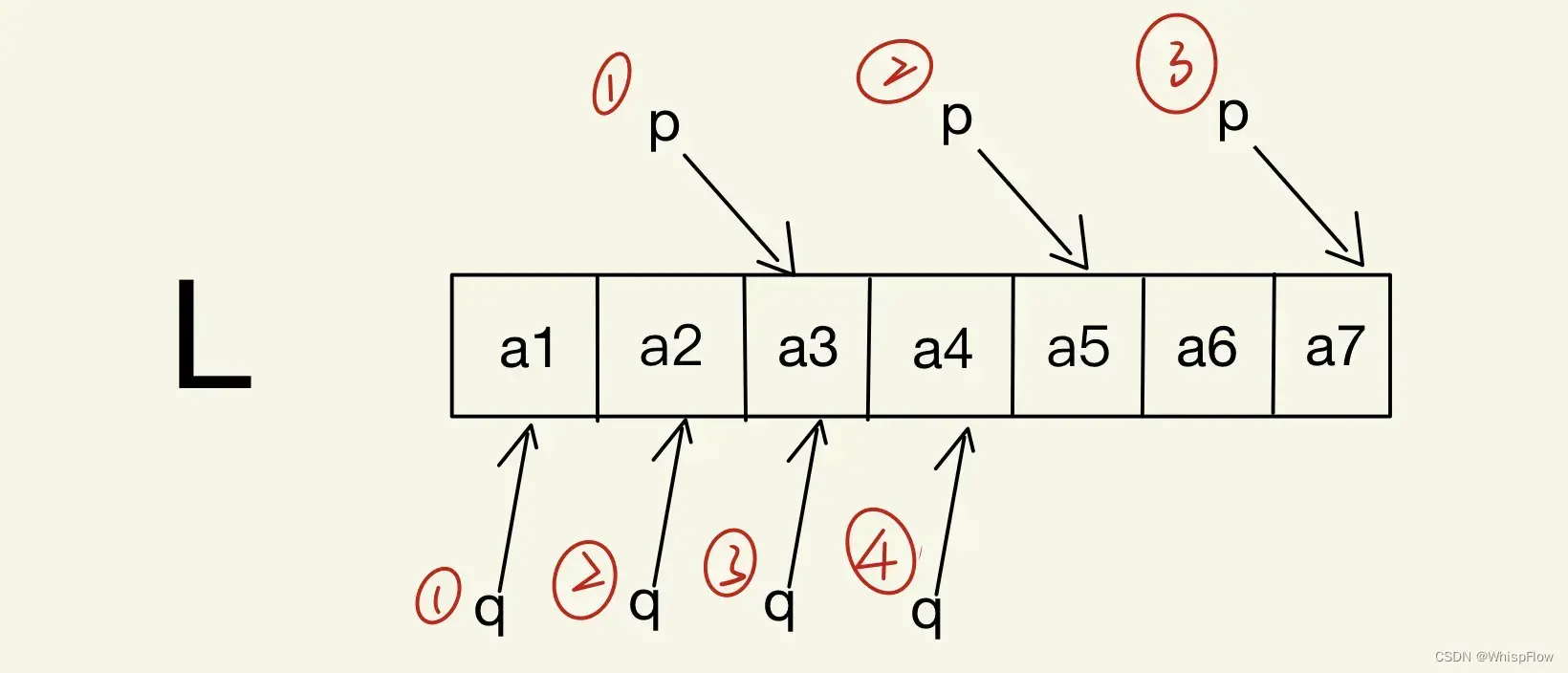
当进入到第四次循环，也就是p->next==NULL的时候，此时q->next指向a4如上图所示。

从q这里断链，L2中的数据自然也就包含a5,a6,a7。

时间复杂度：因为p每次移动两步(即为两个结点)，故其循环的次数就是n/2，忽略首项系数就是O(n)。

注意：但凡涉及到链表的结构修改操作，需要在函数的形参上加上&(取地址符)，C++的引用操作

链表反转(逆置)

//链表反转(逆置)
void list_reverse(LinkList L2) {
	LinkList r, s, t;
	r = L2->next;
	//链表为空的情况
	if (r == NULL) return;
	s = r->next;
	//链表只有一个结点的时候
	if (s == NULL) return;
	t = s->next;
	while (t) {
		s->next = r;//指针反转
		r = s;
		s = t;
		t = t->next;
	}
	s->next = r;
	//逆置后，链表的第一个结点即为尾结点
	L2->next->next = NULL;
	//L2指向现链表的头结点s
	L2->next = s;
}

这里我们用三个指针操控，r,s,t。由于链表的特性，我们只需要改变指针的指向即可完成反转操作。需要判断两种情况。即链表为空的情况和链表只有一个结点的情况。直接返回即可。

这里我们用距离最远的指针t作为循环的结束条件，只要t==NULL,循环即结束。

将s->next指向r，将s赋给r，t赋给s，t=t->next即可完成一次逆置操作，但因为一开始t是领先r两个位置的，故判断t==NULL循环结束时，实际上还有一次逆置操作没有完成，这里我们只需要将r的地址赋给s->next即可，这样便完成了逆置操作。剩下的就是些收尾工作。

注意：原先的链表头结点已经变成了尾结点，我们需要手动将其next置为空

而此时的链表头既是s,将s的地址赋给L2->next即可完成链表逆置的全部工作。

时间复杂度：reverse函数只遍历了L2链表，遍历次数也是n/2,故时间复杂度为O(n)

链表合并

//链表合并
void list_merge(LinkList L, LinkList L2) {
	LinkList p, q, pcur;
	p = L2->next;//p指L2的第一个结点
	pcur = L->next;//pcur始终指向组后的链表
	q = pcur->next;//q指向L1的第一个结点
	while (p && q) {
		pcur->next = p;
		p = p->next;
		pcur = pcur->next;
		pcur->next = q;
		q = q->next;
		pcur = pcur->next;
	}
	//任何一个链表都可能剩余一个结点，放进来即可
	if (p != NULL) {
		pcur->next = p;
	}
	if (q != NULL) {
		pcur->next = q;
	}
}

链表合并操作我们同样需要三个指针，一个指向L，一个指向L2，一个指向L’，循环的条件，判断L和L2链表当前next不为空，因为一开始即对pcur进行赋值为L->next，故往后操作只需要直接让其next指向L2->next也是p即可。个人感觉有点两个字符串交叉合并的意思。

一次操作：

pcur指向p(L2->next),p往后移动一步，再让pcur往后移动一步，让pcur指向q(L->next)，q往后移一步，pcur再往后移动一步

        pcur->next = p;
       p = p->next;
       pcur = pcur->next;
       pcur->next = q;
       q = q->next;
       pcur = pcur->next;

时间复杂度：merge函数while的循环次数也是n/2,故时间复杂度为O(n)

即是以上六步，最后奇数个数据的链表会剩余一个结点的情况，我们直接将其放入新链表L’即可。

以下是全部代码：

#include<stdio.h>
#include<stdlib.h>
//考研链表题练习
typedef int ElemType;
typedef struct Lnode {
	ElemType data;
	struct Lnode* next;
}Lnode, * LinkList;

//尾插法建立链表
void list_tail_insert(LinkList& L) {
	L = (LinkList)malloc(sizeof(Lnode));
	ElemType num;
	LinkList q, p;
	q = L;
	scanf_s("%d", &num);
	while (num != 9999) {
		p = (LinkList)malloc(sizeof(Lnode));
		p->data = num;
		q->next = p;
		q = p;
		scanf_s("%d", &num);
	}
	p->next = NULL;
}
//链表断链
void list_spilt(LinkList L, LinkList& L2) {
	LinkList q, p;
	L2 = (LinkList)malloc(sizeof(Lnode));
	//将p和q进行初始化
	p = q = L->next;
	//需要对当前指针进行判断
	//如果当前指针为空的情况
	//开始遍历
	while (p) {
		p = p->next;
		//防止链表只有一个结点的情况
		if (p == NULL) {
			break;
		}
		p = p->next;
		//为了偶数个的情况进行判断
		if (p == NULL) {
			break;
		}
		q = q->next;
	}
	//L2的相关操作
	//将L2的链表头节点指向当前链表的中间结点q
	L2->next = q->next;
	//将中间结点q的next置为NULL(即为L链表的断链)
	q->next = NULL;
}
//链表反转(逆置)
void list_reverse(LinkList L2) {
	LinkList r, s, t;
	r = L2->next;
	//链表为空的情况
	if (r == NULL) return;
	s = r->next;
	//链表只有一个结点的时候
	if (s == NULL) return;
	t = s->next;
	while (t) {
		s->next = r;//指针反转
		r = s;
		s = t;
		t = t->next;
	}
	s->next = r;
	//逆置后，链表的第一个结点即为尾结点
	L2->next->next = NULL;
	//L2指向现链表的头结点s
	L2->next = s;
}
//链表合并
void list_merge(LinkList L, LinkList L2) {
	LinkList p, q, pcur;
	p = L2->next;//p指L2的第一个结点
	pcur = L->next;//pcur始终指向组后的链表
	q = pcur->next;//q指向L1的第一个结点
	while (p && q) {
		pcur->next = p;
		p = p->next;
		pcur = pcur->next;
		pcur->next = q;
		q = q->next;
		pcur = pcur->next;
	}
	//任何一个链表都可能剩余一个结点，放进来即可
	if (p != NULL) {
		pcur->next = p;
	}
	if (q != NULL) {
		pcur->next = q;
	}
}

//链表输出
void list_printf(LinkList L) {
	L = L->next;
	while (L) {
		printf("%3d ", L->data);
		L = L->next;
	}
}
int main() {
	//建立链表
	LinkList L, L2;
	//尾插法
	list_tail_insert(L);
	list_printf(L);
	//链表断链
	list_spilt(L, L2);
	printf("\n----------------list_spilt-----------------\n");
	list_printf(L2);
	//链表逆置
	list_reverse(L2);
	printf("\n----------------list_reverse---------------\n");
	list_printf(L2);
	//链表合并
	list_merge(L, L2);
	printf("\n----------------list_merge-----------------\n");
	list_printf(L);

	return 0;
}

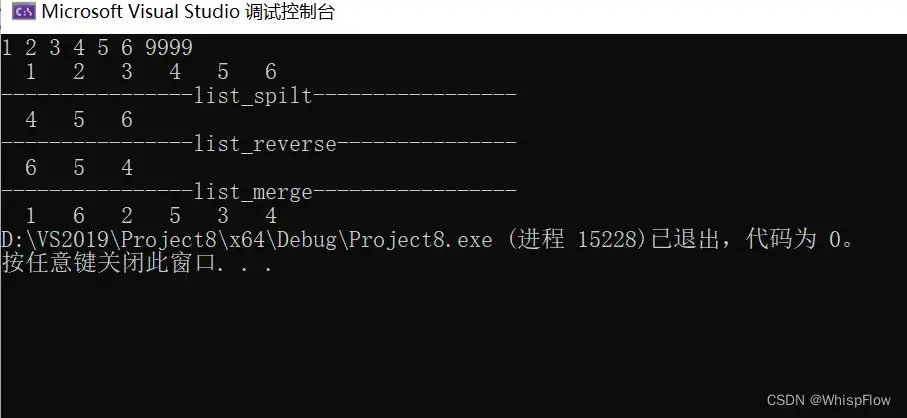
代码效果：

偶数情况:

单数情况：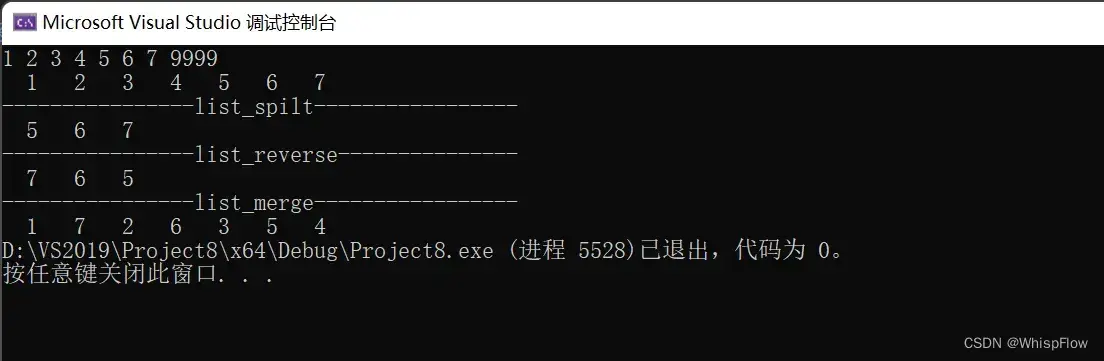

(3)说明你所设计的算法的时间复杂度

以上三个函数总的运行次数为(3/2)n,忽略首项系数，即为O(n)

文章出处登录后可见！

已经登录？立即刷新