智能优化算法:卷积优化算法 2023
摘要:将二维卷积运算引入智能优化算法的种群位置更新过程,提出一种新的智能优化算法,即卷积优化算法(Convolution Optimization Algorithm,COA)。 该算法主要包括卷积搜索和解质量增强 2 种机制:在卷积搜索过程中,分别定义纵向卷积核、横向卷积核和区域卷积核,依次进行二维卷积运算并更新种群的位置向量,然后将 3 种卷积核更新后的种群的位置向量进行随机权重或等比例权重相加,进一步更新种群的位置向量;在解质量增强过程中,对最优解的搜索空间逐维进行带非惯性权重的高斯变异,并对最优解进行扰动,从而提高算法的局部搜索能力。
1.卷积优化算法
COA 主要包括卷积搜索和解质量增强 2 种机制,其中:卷积搜索机制的是通过矩阵卷积运算增强搜索趋势并加快收敛速度,从而在搜索空间中获得更好的位置;解质量增强机制通过提高解的质量,避免每次迭代中出现局部最优。
1.1 种群初始化
在 中, 个体的位置向量
,
) 为优化问题的候选解, 定义
用于在
维空间 中搜索,其中
为决策变量的维度。这样, 在卷积 优化算法中, 种群的位置向量
由维度为
的
个个体组成, 则种群的位置向量
由
阶矩阵 构成,有
在 中, 种群的位置向量
的适应度值为
式中: 表示适应度函数, 也称目标函数。
在 中,初始种群的位置向量
在
维搜 索空间中随机生成, 每个个体的位置向量
的初始 化可定义为
式中: 为一个
阶矩阵, 为第
个个体的下限;
为一个
阶矩阵, 为第
个个体的上限; rand 为
之间的随机数。
1.2 卷积搜索机制
卷积搜索过程分为纵向卷积位置更新、横向卷积位置更新、区域卷积位置更新和综合位置更新 4个步骤。
1.2.1 纵向卷积位置更新
定义纵向卷积核为
式中: 为一个
阶矩阵, 为纵向卷积核, 其中
为纵向卷积核的高, 1 为纵向卷积核的宽;
为一个
阶矩阵,每个元素为
之间的随机 数;
为一个
阶矩阵, 所有元素为 1 。 定义纵向卷积为
式中: 为当前迭代次数;
为一个
阶矩阵, 为 第
代种群的位置向量;
为一个
阶矩阵, 为 第
代纵向卷积位置更新后的种群的位置向量。
比较 和
中每个个体位置的适应度值的大 小,择优替换掉
中个体位置, 则有
式中: 为第
代种群的第
个个体位置;
为 第
代纵向卷积位置更新后的种群的第
个个体 位置。
1.2.2 横向卷积位置更新
定义横向卷积核为
式中: 为一个
阶矩阵, 为横向卷积核, 其中 1 为横向卷积核的高,
为横向卷积核的宽;
为一个
阶矩阵,每个元素为
之间的随机 数;
为一个
阶矩阵,所有元素为 1 。
定义横向卷积为
式中: 为一个
阶矩阵, 为横向卷积更新后的 种群的位置向量。
比较 和
中每个个体位置的适应度值的大 小,择优替换掉
中个体位置,则有
式中: 为第
代横向卷积位置更新后的种群的第
个个体位置。
1.2.3 区域卷积位置更新
定义区域卷积核为
式中: 为一个
阶矩阵, 为区域卷积核, 其中
为区域卷积核的高和宽;
为一个
阶 矩阵,每个元素为
之间的随机数;
为一个
阶矩阵,所有元素为 1 。
定义区域卷积为
式中: 为一个
阶矩阵, 为区域卷积更新后的 种群的位置向量。
比较 和
中每个个体位置的适应度值的大 小,择优替换掉
中个体位置, 则有
式中: 为第
代区域卷积位置更新后的种群的第
个个体位置。
1.2.4 综合位置更新
在综合位置更新阶段, 将第 代纵向卷积更新 后的种群的位置向量
, 第
代横向卷积更新后的 种群的位置向量
和第
代区域卷积更新后的种 群的位置向量
, 采用随机权重或等比例权重相加 合并为
, 即
式中: 均为
之间的随机数, 特别地, 可 以令
, 以便进行等比例权重相加。
比较 和
中每个个体位置的适应度值的大 小,择优替换掉
中个体位置, 则有
式中: 为第
代综合位置更新后的种群的第
个 个体位置。
最后, 计算 中所有个体位置的适应度值, 并根据适应度值的大小进行排序, 选出最优 解
。
1.3 解质量增强机制
在 中,解质量增强机制是对最优解
的
维搜索空间逐维进行带非惯性权重的高斯变异, 对最优解
进行扰动, 从而提高算法的局部搜 索能力。
对最优解 中
维搜索空间逐维进行带非惯性权重的高斯变异, 则有
式中: 为一个
阶 矩阵, 为最优解
中
维搜索空间中的第
,
维的位置;
, 其中 iter
为最大迭代次数; randn 为一个满足均值为 0 , 方差 为 1 的标准正态分布的随机数;
为一个
阶矩阵, 为对最优解
的第
维进行带非惯性权重 高斯变异后的第
维位置。
令对第 维进行带非惯性权重高斯变异后的个 体位置为
, 比较
和
的适应度值的大 小,择优替换掉
的个体位置,则有
运行过程的伪代码如下:
输人: 种群大小为 , 个体位置的维度为
, 最大 迭代次数为 iter
, 卷积核参数为
和适应度函数为
输出:最优解及其位置
1 : 初始化种群, 计算每个个体位置的适应度值, 选出最优个体的适应度值及其位置
2 : While iter
do
3 : 在纵向卷积位置更新阶段, 由式 (4)- (6) 更 新种群的位置向量
4 : 在横向卷积位置更新阶段, 由式 (7)- (9) 更 新种群的位置向量
5 : 在区域卷积位置更新阶段, 由式 (10)-(12) 更新种群的位置向量
6 : 在综合位置更新阶段, 由式 (13)、(14) 更新 种群的位置向量
7 : 计算种群个体位置的适应度值, 选出最优解
8 : for to
do
9 : 在解增强阶段, 由式 (15)、(16) 更新最优解 及其位置
10 : end for
11 : 更新全局最优解及其位置
13 : end while
2.实验结果
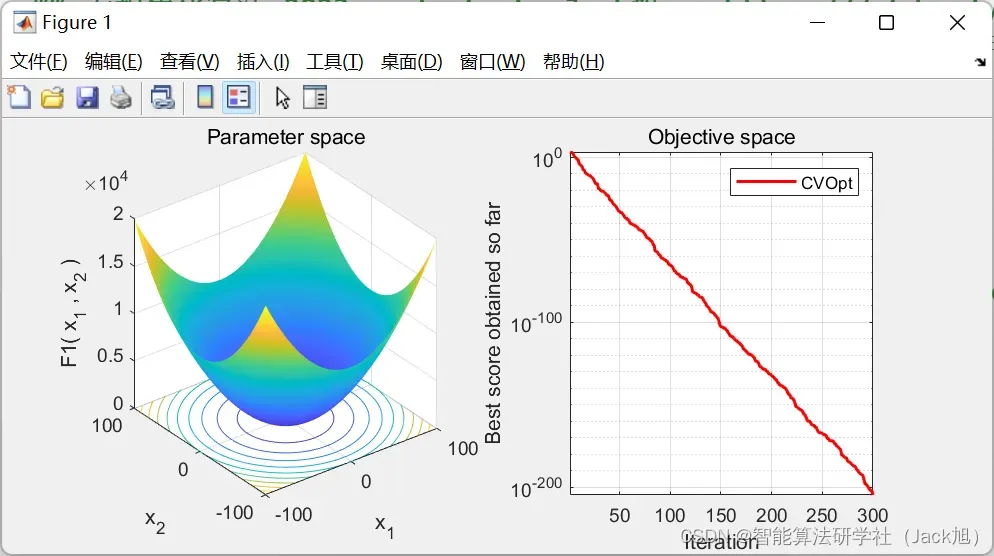
3.参考文献
[1]陈克伟,魏曙光,张嘉曦.基于二维卷积运算的智能优化算法[J].装甲兵学报,2023,2(01):102-108.
4.Matlab
5.Python
文章出处登录后可见!
