quality focal loss & distribute focal loss 解说（附代码）

参见generalized focal loss paper
其中包含有Quality Focal Loss 和 Distribution Focal Loss。

目录

• • Quality Focal Loss
  • Distribute Focal Loss

Quality Focal Loss

先来说一下Quality Focal Loss,
在这之前，先要了解一下Focal Loss, 在这篇文章里有写过。
它主要是解决class imbalance，同时降低容易分类的weight，使训练更集中到难分类的上面

我们从cross entropy入手：
cross entropy的公式如下：

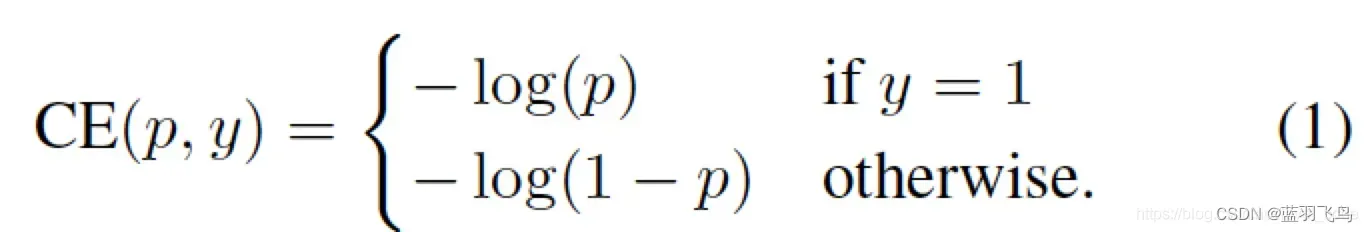
把其中的y=1时为p, y=0时1-p 写成一个

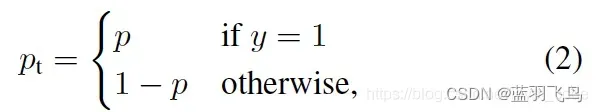
那么，cross entropy可以简化为：

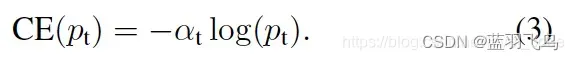
降低容易分类的weight, 比如时，很容易分类，降低它的weight, 同时结合解决class imbalance的问题。
这个就是Focal Loss的公式。

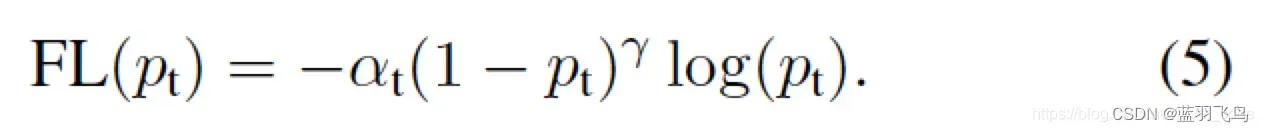
现在有一个问题，就是（1）训练集和测试集的用途是不同的，训练集单独用来训练，却和测试集一起在现实中做推理。而且supervision只用于positive sample, 但是有时negative sample会有更高的score

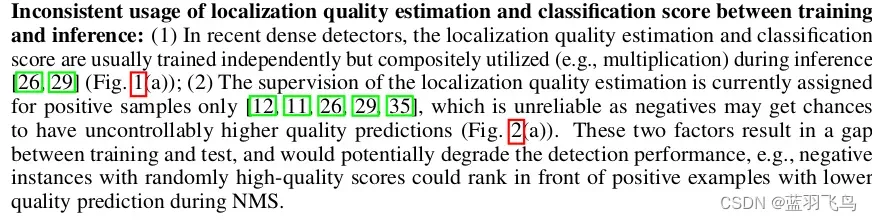
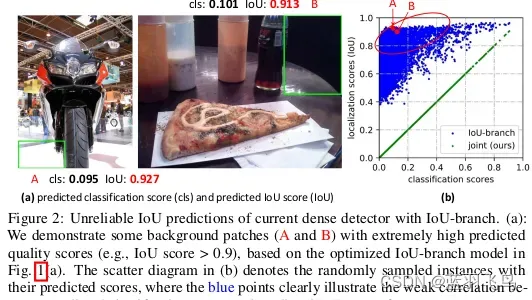
背景的IOU可能比positive sample还要大，所以作者把IOU和分类的score结合起来，
而且把one-hot label给soft化，具体就是把label的1 乘以 IOU，
这里的IOU是指预测出的bounding box和与之匹配的ground truth box的IOU。范围在0~1之间。
理论上来说一个预测box会匹配一个gt_box, 当匹配多个时，取cost最小的那个。

至于如何匹配，就是计算一张图片中有效的（自己定义）预测box和这张图片所有的ground truth box的IOU，
再取IOU>阈值的box作为最终预测的box。
每个box还会有一个class score.

class score经过sigmoid运算后就是公式中的
公式中的是label乘以对应的IOU。

为了解决class imbalance的问题，还需要结合Focal Loss,
但是Focal Loss的label是0，1，而这里的soft label是小数，
所以把Focal Loss中的两项做一下扩展：

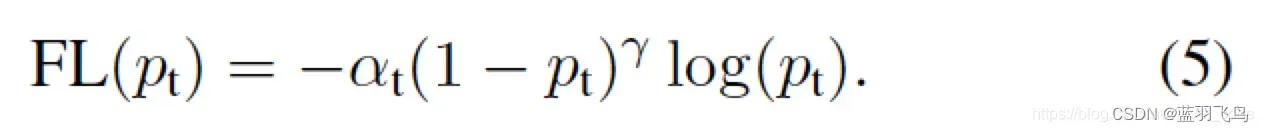
因此得到最后的QFL公式：

具体看下代码：

def quality_focal_loss(pred, target, beta=2.0):
    r"""Quality Focal Loss (QFL) is from `Generalized Focal Loss: Learning
    Qualified and Distributed Bounding Boxes for Dense Object Detection
    <https://arxiv.org/abs/2006.04388>`_.

    Args:
        pred (torch.Tensor): Predicted joint representation of classification
            and quality (IoU) estimation with shape (N, C), C is the number of
            classes.
        target (tuple([torch.Tensor])): Target category label with shape (N,)
            and target quality label with shape (N,).
        beta (float): The beta parameter for calculating the modulating factor.
            Defaults to 2.0.

    Returns:
        torch.Tensor: Loss tensor with shape (N,).
    """
    assert (
        len(target) == 2
    ), """target for QFL must be a tuple of two elements,
        including category label and quality label, respectively"""
    # label denotes the category id, score denotes the quality score
    label, score = target  #label:gt label,score:gt score(IOU),

    # negatives are supervised by 0 quality score
    #pred:预测的class score
    pred_sigmoid = pred.sigmoid() #sigmoid:1/(1+e^-x)
    scale_factor = pred_sigmoid
    zerolabel = scale_factor.new_zeros(pred.shape) #全0
    #label全为0时的qfl loss,即先把背景的loss填上
    loss = F.binary_cross_entropy_with_logits( #等价于sigmoid+binary entropy, 更稳定
        pred, zerolabel, reduction="none"
    ) * scale_factor.pow(beta)

    # FG cat_id: [0, num_classes -1], BG cat_id: num_classes
    bg_class_ind = pred.size(1)  #背景的下标
    #label是前景的下标,注意这是gt label
    pos = torch.nonzero((label >= 0) & (label < bg_class_ind), as_tuple=False).squeeze(
        1
    )
    pos_label = label[pos].long()  #取出下标对应的前景gt label
    # positives are supervised by bbox quality (IoU) score
    scale_factor = score[pos] - pred_sigmoid[pos, pos_label] #公式中的(y-sigma)
    #在有前景的对应位置填上gfl的前景loss
    loss[pos, pos_label] = F.binary_cross_entropy_with_logits(
        pred[pos, pos_label], score[pos], reduction="none"
    ) * scale_factor.abs().pow(beta) #公式中的QFL(sigma)不要负号

    loss = loss.sum(dim=1, keepdim=False) 
    return loss

Distribute Focal Loss

再来说Distribution focal loss

一般来说，预测值x 和真实标签y 之间，是假设的Dirac delta分布，即

这表示预测值x 总有一个标签y与之对应。

那么将它与x相乘就能复原标签y.

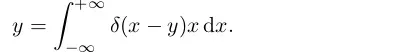
如果已经给出了y的范围，就能限制住积分的上下限。

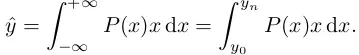
连续变离散（比如每间隔1取一次值）。

P(x)是网络输出经过softmax处理后的结果，但是P(x)可以有不同的分布，
公式(5) 中可以看到能得到y 的不同组合很多，例如下图

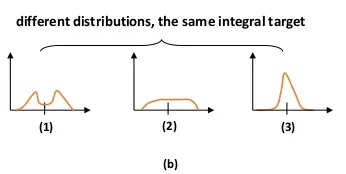
直观上来看，分布(3)得到标签y的准确性更高，
因此就推出 要把预测的P(x) 尽可能地在 y 处有较大的概率。
因此就取靠近y 的两个label, 和 ,

类似GFL公式，同时不需要考虑class imbalance, 所以只需取cross entropy的那一项：

def distribution_focal_loss(pred, label):
    r"""Distribution Focal Loss (DFL) is from `Generalized Focal Loss: Learning
    Qualified and Distributed Bounding Boxes for Dense Object Detection
    <https://arxiv.org/abs/2006.04388>`_.

    Args:
        pred (torch.Tensor): Predicted general distribution of bounding boxes
            (before softmax) with shape (N, n+1), n is the max value of the
            integral set `{0, ..., n}` in paper.
        label (torch.Tensor): Target distance label for bounding boxes with
            shape (N,).

    Returns:
        torch.Tensor: Loss tensor with shape (N,).
    """
    dis_left = label.long()
    dis_right = dis_left + 1
    weight_left = dis_right.float() - label
    weight_right = label - dis_left.float()
    loss = (
        F.cross_entropy(pred, dis_left, reduction="none") * weight_left
        + F.cross_entropy(pred, dis_right, reduction="none") * weight_right
    )
    return loss