文章目录
- 余弦相似度简介
- 余弦相似度原理
- 文本分析应用余弦相似度
- 余弦相似度的计算
- numpy
- 向量与向量
- 向量与矩阵
- 矩阵与矩阵
- scipy
- 向量与向量
- sklearn
- 向量与向量
- 向量与矩阵
- 矩阵与矩阵
- 英文文本计算余弦相似度
- 第一步,定义文档
- 第二步,文本向量化
- 计算余弦相似度
- 中文文本计算余弦相似度——以MD&A文本为例
- 实证论文
本文首发于微信公众号:Python for Finance
链接:https://mp.weixin.qq.com/s/i74pct7a4NBRSN39kg2NXA
余弦相似度简介
余弦相似度原理

余弦相似性通过计算两个向量的余弦角来测量两个向量之间的相似性。
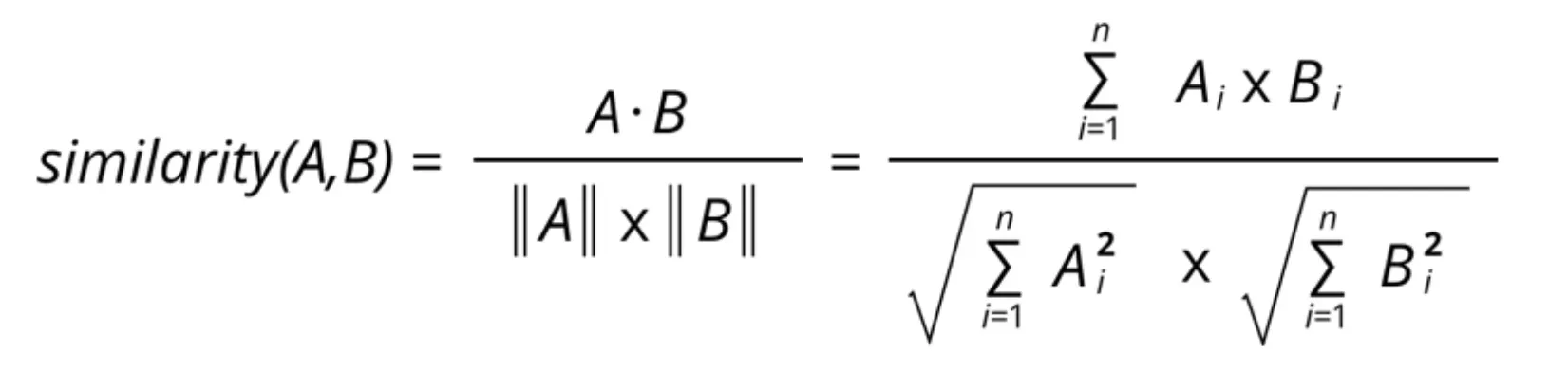
文本分析应用余弦相似度
D1 = ‘the best data science course’
D2 = ‘data science is popular’
基于词袋法构造文本向量:
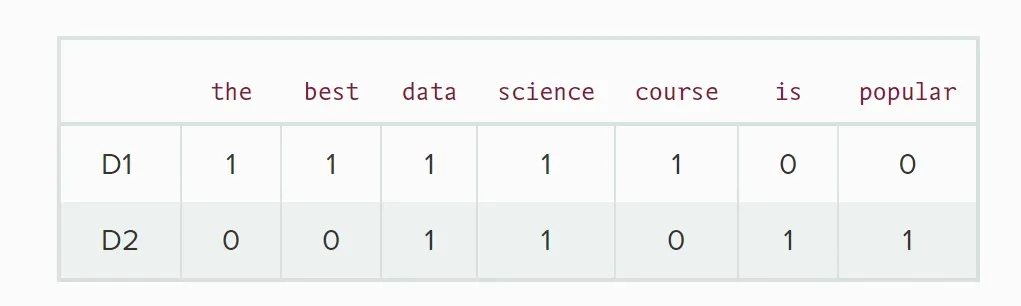
D1:[1,1,1,1,1,0,0]
D2:[0,0,1,1,0,1,1]
第一步,计算点积
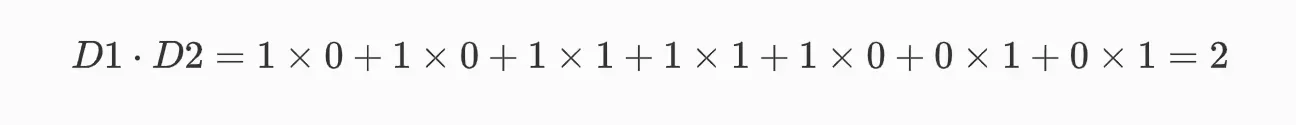
第二步,计算模长
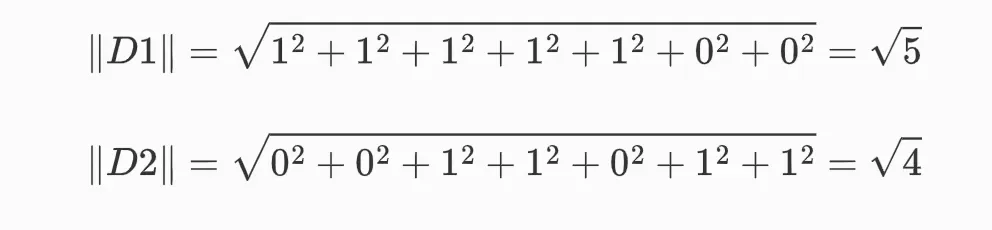
第三步,计算余弦相似度
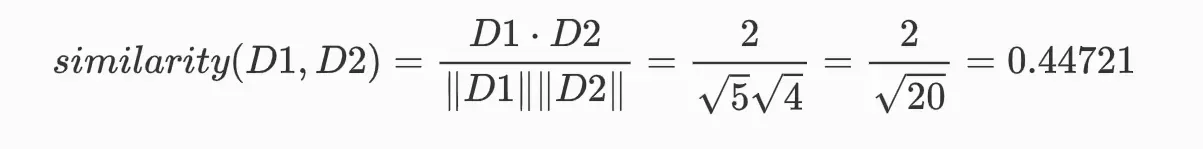
余弦相似度的计算
numpy
向量与向量
import numpy as np
from numpy.linalg import norm
A = np.array([2,1,2])
B = np.array([3,4,2])
cosine = np.dot(A,B)/(norm(A)*norm(B))
print("余弦相似度:", cosine)
结果为:
余弦相似度: 0.8665782448262421
向量与矩阵
import numpy as np
from numpy.linalg import norm
A = np.array([[1,2,2],
[3,2,2],
[-2,1,-3]])
B = np.array([3,4,2])
cosine = np.dot(A,B)/(norm(A, axis=1)*norm(B))
print("余弦相似度:\n", cosine)
结果为:
余弦相似度:
[ 0.92847669 0.94579243 -0.39703333]
注意,A有三个向量,B是一个向量。我们得到了余弦相似度数组中的三个元素。第一元素对应于A的第一个向量(第一行)和向量B之间的余弦相似性。第二个元素对应于A的第二个向量(第二行)和向量B之间的余弦相似性。第三个元素也是如此。
矩阵与矩阵
import numpy as np
from numpy.linalg import norm
A = np.array([[1,2,2],
[3,2,2],
[-2,1,-3]])
B = np.array([[4,2,4],
[2,-2,5],
[3,4,-4]])
cosine = np.sum(A*B, axis=1)/(norm(A, axis=1)*norm(B, axis=1))
print("余弦相似度:\n", cosine)
结果为:
余弦相似度:
[0.88888889 0.5066404 0.41739194]
最后得到的相似度数组的意义:
- 第一个元素代表的是
A中的第一行和B中的第一行的余弦相似度 - 第二个元素代表的是
A中的第二行和B中第二行的余弦相似度 - 第三个元素代表的是
A中的第二行和B中第二行的余弦相似度
如何获得A和B的任意两行之间的余弦相似性呢?
import numpy as np
from numpy.linalg import norm
A = np.array([[1,2,2],
[3,2,2],
[-2,1,-3]])
B = np.array([[4,2,4],
[2,-2,5],
[3,4,-4],
[2,5,9]])
norm1 = norm(A,axis=-1,keepdims=True)
norm2 = norm(B,axis=-1,keepdims=True)
arr1_norm = A / norm1
arr2_norm = B / norm2
cos = np.dot(arr1_norm,arr2_norm.T)
print(cos)
结果为:
[[ 0.88888889 0.46420708 0.15617376 0.95346259]
[ 0.9701425 0.5066404 0.34089931 0.78624539]
[-0.80178373 -0.97700842 0.41739194 -0.66254135]]
最后得到的相似度矩阵的意义:
- 因为
A是 3 行,B是 4 行,因此最终的输出矩阵维度是3 行 4 列 - 第一行代表的是
A中的第一行和B中的每一行的余弦相似度 - 第二行代表的是
A中的第二行和B中每一行的余弦相似度
scipy
向量与向量
from scipy import spatial
A = np.array([2,1,2])
B = np.array([3,4,2])
cos_sim = 1 - spatial.distance.cosine(A, B)
print(cos_sim)
sklearn
向量与向量
from sklearn.metrics.pairwise import cosine_similarity
import numpy as np
# 向量表示为二维数组的形式,推荐使用
A = np.array([[1,2,2]])
B = np.array([[3,2,2]])
cos_sim = cosine_similarity(A, B)
print(cos_sim)
# 向量表示为一维数组的形式
A = np.array([1,2,2])
B = np.array([3,2,2])
cos_sim = cosine_similarity([A, B])
print(cos_sim)
结果为:
[[0.88929729]]
[[1. 0.88929729]
[0.88929729 1. ]]
向量与矩阵
from sklearn.metrics.pairwise import cosine_similarity
import numpy as np
A = np.array([[1,2,2],
[3,2,2],
[-2,1,-3]])
B = np.array([[4,2,4]])
cosine = cosine_similarity(A,B)
print("余弦相似度:\n", cosine)
结果为:
余弦相似度:
[[ 0.88888889]
[ 0.9701425 ]
[-0.80178373]]
矩阵与矩阵
from sklearn.metrics.pairwise import cosine_similarity
import numpy as np
A = np.array([[1,2,2],
[3,2,2],
[-2,1,-3]])
B = np.array([[4,2,4],
[2,-2,5],
[3,4,-4],
[2,5,9]])
cosine = cosine_similarity(A) # A中的行向量之间的两两余弦相似度,等价于cosine = cosine_similarity(A,A)
print("余弦相似度:\n", cosine)
cosine = cosine_similarity(A,B) # 第一行代表的是A中的第一行和B中的每一行的余弦相似度;第二行代表的是A中的第二行和B中每一行的余弦相似度
print("余弦相似度:\n", cosine)
使用cosine_similarity,传入一个变量a时,返回数组的第i行第j列表示a[i]与a[j]的余弦相似度;传入两个变量a,b时,返回的数组的第i行第j列表示a[i]与b[j]的余弦相似度。
结果为:
余弦相似度:
[[ 1. 0.88929729 -0.53452248]
[ 0.88929729 1. -0.64820372]
[-0.53452248 -0.64820372 1. ]]
余弦相似度:
[[ 0.88888889 0.46420708 0.15617376 0.95346259]
[ 0.9701425 0.5066404 0.34089931 0.78624539]
[-0.80178373 -0.97700842 0.41739194 -0.66254135]]
英文文本计算余弦相似度
第一步,定义文档
# 定义文档
doc1 = 'The sun is the largest celestial body in the solar system'
doc2 = 'The solar system consists of the sun and eight revolving planets'
doc3 = 'Ra was the Egyptian Sun God'
documents = [doc1, doc2, doc3]
第二步,文本向量化
本例采用词袋模型进行文本向量化,也可采用TF-IDF模型。
from sklearn.feature_extraction.text import CountVectorizer
import pandas as pd
# 词袋模型:文本向量化
count_vectorizer = CountVectorizer(stop_words='english')
sparse_matrix = count_vectorizer.fit_transform(documents)
# 文本向量化的可视化表格
doc_term_matrix = sparse_matrix.todense()
df = pd.DataFrame(doc_term_matrix,
columns=count_vectorizer.get_feature_names(),
index=['doc1', 'doc2', 'doc3'])
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ngPpthcD-1675524259020)(https://python-for-finance.oss-cn-hangzhou.aliyuncs.com/202302042219303.png)]
计算余弦相似度
from sklearn.metrics.pairwise import cosine_similarity
print(cosine_similarity(df))
结果为:
[[1. 0.4 0.2236068]
[0.4 1. 0.2236068]
[0.2236068 0.2236068 1. ]]
中文文本计算余弦相似度——以MD&A文本为例
我们来看一下中文情境下余弦相似度如何计算,主要多了一个分词的步骤。在这里,我们使用到了 CNRDS 数据库中关于 MDA 的 10 个样本数据,如需完整的 MDA 数据请到 CNRDS 数据库中下载。
import pandas as pd
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics.pairwise import cosine_similarity
import jieba
import re
# 调用数据
data = pd.read_excel(r"C:\Users\chenwei\Downloads\管理层讨论与分析\管理层讨论与分析.xlsx")
stopwords = pd.read_csv(r"C:\Users\chenwei\Downloads\stopwords-master\stopwords-master\cn_stopwords.txt", names=["stopwords"])
# 定义分词函数
def cut_words(text):
words_list = []
# 只保留中文内容
text = ''.join(re.findall('[\u4e00-\u9fa5]+', text))
words = jieba.lcut(text)
for word in words:
if word not in list(stopwords["stopwords"]):
words_list.append(word)
return " ".join(words_list)
# 对文本分词
data["经营讨论与分析内容"] = data["经营讨论与分析内容"].apply(cut_words)
data

在这里,我们需要注意的是要设置token_pattern,这个参数接受正则表达式。默认情况下会忽略1个字符(但是在中文的情况下就不能忽略一个字符)
- token_pattern(默认参数) : r”(?u)\b\w\w+\b”
- token_pattern(修改之后) : r”(?u)\b\w+\b”
计算两两之间的文本相似度
# 基于词集法构造文本向量计算余弦相似度
# 实例化词集法vectorizer
vectorizer = CountVectorizer(token_pattern=r"(?u)\b\w+\b",binary=True)
# 将语料集转化为词集向量
vec = vectorizer.fit_transform(data["经营讨论与分析内容"])
# 计算余弦相似度
CS_SoW = cosine_similarity(vec)
# 基于词袋法构造文本向量计算余弦相似度
# 实例化词袋法vectorizer
vectorizer = CountVectorizer(token_pattern=r"(?u)\b\w+\b")
# 将语料集转化为词袋向量
vec = vectorizer.fit_transform(data["经营讨论与分析内容"])
# 计算余弦相似度
CS_BoW = cosine_similarity(vec)
# 基于TF-IDF方法构造文本向量计算余弦相似度
# 实例化TF-IDF法vectorizer
vectorizer = TfidfVectorizer(token_pattern=r"(?u)\b\w+\b")
# 将语料集转化为TF-IDF向量
vec = vectorizer.fit_transform(data["经营讨论与分析内容"])
# 计算余弦相似度
CS_TFIDF = cosine_similarity(vec)
实证论文
潘欣,余鹏翼,苏茹,王琳.并购重组业绩承诺与企业融资约束——基于文本分析的经验证据[J].管理评论,2022,34(03):268-277.
第三,利用余弦相似度计算样本与对应年份融资约束集的相似度。首先将每一年的 MD&A 样本和对应 年份的融资约束文本集进行整合,利用 python 中的 jieba 库对整合后的样本进行分词,由于分词效果对下文 TF-IDF 算法结果具有重要影响,本文采用 github① 上提供的哈工大停用词、四川大学机器智能实验室停用词、 百度停用词、中文停用词以及最全中文停用词表整合后的 2462 个新中文停用词列表,优化分词效果。然后根 据分词后的词频提取特征,也即建立词频向量。考虑分词后词频矩阵变大,词频向量会变得非常稀疏,本文采 用 TF-IDF 算法,也即词频-逆文档频率,先计算出关键词的 TF-IDF 值,然后使用 TF-IDF 矩阵进行余弦相似度 计算,最终得到每年单个样本与对应年度融资约束文本集的相似度 ConstrainedSimilarity
①https://github.com/goto456/stopwords。
第四,考虑到不同的 MD&A 文本中会因章节标题、固定格式、行业专有名词和术语等存在共性内容,为了 剔除行业和上市公司所在板块要求信息披露方式的影响,本文先将每年的 MD&A 文本按照 2012 年证监会行 业分类代码进行划分,对应年度的融资约束文本集也按照行业进行划分,然后按照上述方法同理计算每年单 个样本 MD&A 文本与当年对应行业融资约束文本集的相似度,最终获得 IndSimilarity 值,该值即为 MD&A 文 本与对应年度融资约束文本集因行业共性内容导致的相似度。同理得到因板块信息披露方式相同而导致的 相似度 BoardSimilarity 值。
张勇,殷健.会计师事务所联结与企业会计政策相似性——基于TF-IDF的文本相似度分析[J].审计研究,2022(01):94-105.
1.会计政策相似性的度量
参考 Brown和 Tucker(2011)的方法,本文采用余弦相似度和欧氏距离来衡量两公司间会计政策文本的 相似度。计算步骤如下 :
(1)利用 Python中 jieba分词工具,对每家公司的会计政策文本进行分词,并将分词后的会计政策文本制作成词袋,然后利用该词袋将处于同年度同行业所有公司的会计政策文本制作成语料库。
(2)计算得到词频 TF。
(3)利用“逆文档频率”(IDF)对 TF进 行加权。如果含有特定词 i的文本数量较多,那么特定词 i的 IDF值较低,即权重较低。
(4)将“词频”(TF)和“逆文 档频率”(IDF)相乘,得到特定词 i的 TF-IDF值。如果某个特定词的 TF-IDF值越大,则表示其对文本的重 要性越高,越能有效衡量特定词对单个文本内容的信息含量,以及特定词在语料库中对不同文本内容信息 的区分程度。
(5)将公司 i的会计政策文本与同年度同行业其他公司 {j}的会计政策文本进行配对,分别计 算出配对文本的余弦相似度和欧氏距离作为配对公司会计政策文本的相似度。其中余弦相似度以 TiCos来 表示,欧氏距离以 TiEud来表示,需要说明的是,本文通过取相反数对欧式距离进行了 趋同化处理。趋同化处理后的欧式距离越大,表示文本相似度越高。
[1]李成刚,贾鸿业,赵光辉,付红.基于信息披露文本的上市公司信用风险预警——来自中文年报管理层讨论与分析的经验证据[J/OL].中国管理科学:1-14[2023-02-03].https://doi.org/10.16381/j.cnki.issn1003-207x.2020.2263.
3.3.1 文本相似度计算
文本相似度是衡量文本内容与上一年份 披露信息的相似程度。本文借鉴Dyer等(2017) [19]的方法,采用粘性(Stickiness)指标表示 衡量文本相似度。粘性(Stickiness)是指本 年度文本内容中与上一年度相重复的词汇或 短语。重复词汇越多,相似度越高。本文采 用空间向量模型(VSM)的 TF-IDF 方法,计 算 MD&A 前后两年粘性(Stickiness)词汇数 量,用文本相似度(Sim)进行表示。具体计 算过程如下:首先,计算分词后的文本词项 的 TF-IDF 值;然后,将 MD&A 中的文本通 过向量的形式表示出来,向量元素为句子中 经过分词后的词语出现的频率,若前后两年都出现了该词汇即为粘性 (Stickiness)词汇;最后,通过计算向量间 的余弦角比较前后两年 MD&A 的相似程度。
文章出处登录后可见!
