线性回归预测模型
- 一元线性回归
- 一元线性回归图
- 一元线性回归参数
- 多元线性回归
- 分类变量的处理
- 回归模型的假设性检验
- 模型的显著性检验——F检验
- 回归系数的显著性检验——t检验
- 回归模型的诊断
- 正态性检验
- 直方图法
- PP图与QQ图
- Shapiro检验和K-S检验
- 多重共线性检验
- 线性相关检验
- 独立性检验
- 方差齐性
- BP检验
本文介绍的是线性回归方程的预测模型的学习笔记,将重点记录python的实现过程,对于线性模型的数学推导将不做赘述。若是在本科数学建模比赛中,不必对模型的健壮性做过于冗长的说明;若是数据挖掘类竞赛或项目,则需要最大限度地保障模型的健壮性。
仅用于个人学习过程记录笔记使用
Reference:《从零开始学习Python数据分析与挖掘》
一元线性回归
一元线性回归图
最基础的线性模型固然是一元线性回归。其基本形式想必都无比熟悉,则不做过多的叙述。先看下面这段代码:
import pandas as pd
import seaborn as sns
# 拟合图象的绘制
income = pd.read_csv(r'Salary_Data.csv')
sns.set(color_codes=True)
sns.lmplot(x = 'YearsExperience', y = 'Salary', data = income)
输出结果:
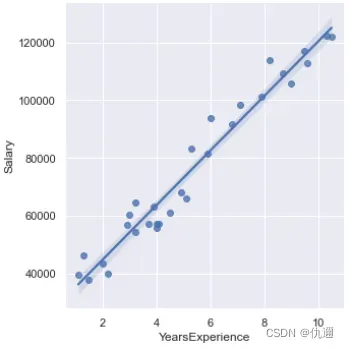
显然,这是一个一元线性回归方程的拟合图象,图像内包括了数据散点、置信区间以及一元线性回归的直线图。接下来让我们解析一下这段代码:
① 、首先是包的导入,本段代码用到的包包括:基本的数据操作pandas包,以及一元线性回归可视化所使用的seaborn库。前者主要用于导入数据,后者用于回归关系的可视化画图。
②、pandas导入数据自不多说,重点看看回归分析可视化lmplot为seaborn库中进行绘制回归图的函数,其中x, y分别规定横纵坐标的标签,data为指定的数据。这里的数据是两组数据集,分别是自变量和因变量。
*注意:若无需执行区间,可再lmplot()函数中加入参数:ci = None。
一元线性回归参数
import statsmodels.api as sm
fit = sm.formula.ols('Salary ~ YearsExperience', data = income).fit()
print(fit.params)
输出结果:
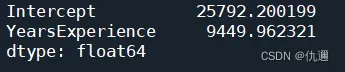
求解一元线性回归方程的参数的方法有很多,可以从最基本的最小二乘拟合入手,即从公式层面上对参数进行计算,但这在编程上会比较麻烦。python为我们提供的众多库可以使得我们更加方便地进行计算参数。下面让我们来解释一下开头的代码:
①、仍然先看导入的库:statsmodels.api 是python提供的用于回归分析的库。我们接着往下看。
②、fit = sm.formula.ols().fit():这里相当于通过最小二乘法拟合出了一元回归模型,总体来看它是一个对象(关于对象的概念可查阅关于面向对象编程相关资料),ols()函数内需要指定自变量和因变量,以及数据的来源。
③、输出结果:从上至下分别是:常数项,自变量YearsExperience的系数。
多元线性回归
相比于一元线性回归,在实际的项目中,多个预测变量和一个响应变量的形式则更加常见。来到多元回归模型这里,我们就要应用到一个新的库——sklearn。这是python提供的应用于机器学习的非常适合新手的库,除了回归模型外还适合于分类、回归、聚类模型等。
本节需要引入的模块:
from sklearn import model_selection # 提供划分训练集预测集的工具
import seaborn as sns # 提供绘制回归图象的工具
import statsmodels.api as sm #提供拟合回归系数的工具
通过调用train_test_split函数进行测试集和训练集的划分,train_test_split(需要划分的数据集,测试集占比,随机数种子固定)
# 划分训练集和测试集
train, test = model_selection.train_test_split(Profit,
test_size = 0.2, random_state = 520)
接下来利用最小二乘法进行拟合,ols的使用方法与一元线性回归方程的计算相同。最后调用params即可输出拟合系数。
model = sm.formula.ols('Profit ~ RD_Spend + Administration + Marketing_Spend + C(State)',
data = train).fit()
print('模型的偏回归系数分别为:\n', model.params)
也可通过model.summary()直接输出该拟合的模型的摘要信息:
print(model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: Profit R-squared: 0.970
Model: OLS Adj. R-squared: 0.965
Method: Least Squares F-statistic: 213.6
Date: Sun, 30 Oct 2022 Prob (F-statistic): 3.94e-24
Time: 10:03:52 Log-Likelihood: -399.26
No. Observations: 39 AIC: 810.5
Df Residuals: 33 BIC: 820.5
Df Model: 5
Covariance Type: nonrobust
========================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------------
Intercept 5.197e+04 6139.987 8.464 0.000 3.95e+04 6.45e+04
C(State)[T.Florida] -3860.6179 3032.491 -1.273 0.212 -1e+04 2309.031
C(State)[T.New York] -1528.0233 2798.053 -0.546 0.589 -7220.705 4164.658
RD_Spend 0.7898 0.040 19.824 0.000 0.709 0.871
Administration -0.0118 0.045 -0.262 0.795 -0.103 0.080
Marketing_Spend 0.0262 0.015 1.730 0.093 -0.005 0.057
==============================================================================
Omnibus: 0.320 Durbin-Watson: 1.813
Prob(Omnibus): 0.852 Jarque-Bera (JB): 0.024
Skew: -0.055 Prob(JB): 0.988
Kurtosis: 3.054 Cond. No. 1.48e+06
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.48e+06. This might indicate that there are
strong multicollinearity or other numerical problems.
接下来进行预测,设置test_X将原数据集的响应变量删除,作为预测数据集。调用模型的predict函数进行预测,并输出结果。
test_X = test.drop(labels = 'Profit', axis = 1)
pred = model.predict(exog = test_X)
print('对比预测值和实际值的差异:\n', pd.DataFrame({'Prediction': pred, 'Real': test.Profit}))
分类变量的处理
在本例中,数据集存在分类变量,在对分类变量进行预测时若不进行处理则会出现在不同类别下的多个回归系数。在建模时系统将分类变量当成了哑变量进行处理,一般来说三个分类最终会出现两个回归系数,剩下的那个就作为参照组。
由于建模时无法指定哑变量的参照组,这可能带来一些隐患。对此将利用pandas模块中的get_dummies函数生成哑变量,然后将所需的对照组对应的哑变量删除即可。代码如下
dummies = pd.get_dummies(Profit.State) # 对数据集中分类变量进行处理
Profit_New = pd.concat([Profit, dummies], axis = 1) # 将原来的数据集和处理好的哑变量 进行合并
Profit_New.drop(labels = ['State', 'New York'], axis = 1, inplace = True) # 删除对照组中的哑变量
train, test = model_selection.train_test_split(Profit_New, test_size = 0.2, random_state=1234)
# 建模
model2 = sm.formula.ols('Profit ~ RD_Spend + Administration + Marketing_Spend + Florida + California', data = train).fit()
print('模型的偏回归系数为:\n', model2.params)
最后,也可以通过model2.summary()进行摘要信息的读取,这会更加常用。
回归模型的假设性检验
回归模型的检验目的是为了检验模型是否有效,包括了模型总体是否有效以及其中单个变量是否具有统计学意义。
模型的显著性检验——F检验
Step1 提出假设
原假设:偏回归系数全为0,即不存在自变量可以构成因变量的线性组合。
Step2 构造统计量

python计算F统计量的函数:回归模型拟合后,调用model.fvalue即可输出,同时,可通过引入scipy.stats模块计算f的理论值。dfn为自由度,n为样本数量。
model.fvalue
from scipy.stats import f
p = model.df_model
n = train.shape[0]
F_Theroy = f.ppf(q = 0.95, dfn = p, dfd = n - p - 1)
print('F的理论分布值:', F_Theroy)
**结果:**通常来说,F的实际值大于理论值,则会拒绝原假设,即模型是显著的。
回归系数的显著性检验——t检验
t检验同样有原假设,即:变量不具有统计学意义。
t检验在python中的操作很简单,只需要通过调用模型摘要:model.summary()即可看到每个变量的p值。p小于0.05的话则说明在95%的置信水平下,该变量具有统计学意义。同样的前文提到的F统计也可以通过模型摘要得到。
关于t检验的数学推导不做赘述。
回归模型的诊断
当模型建立完成后,为了验证模型的健壮性,还可以对模型进行诊断工作,来判断模型是否合理。诊断也是非常重要的,一些诊断甚至能够说明该数据集不适合使用线性回归模型拟合,所以不容小觑!
正态性检验
模型的前提假设是对残差项要求服从正态分布,实质就是要求因变量服从正态分布。
直方图法
import scipy.stats as stats # 导入模块
sns.distplot(a = Profit_New.Profit, bins = 10, fit = stats.norm, norm_hist = True,
hist_kws = {'color': 'steelblue', 'edgecolor': 'black'},
kde_kws = {'color': 'black', 'linestyle': '--', 'label' : '核密度曲线'},
fit_kws = {'color': 'red', 'linestyle': ':', 'label': '正态核密度曲线'})
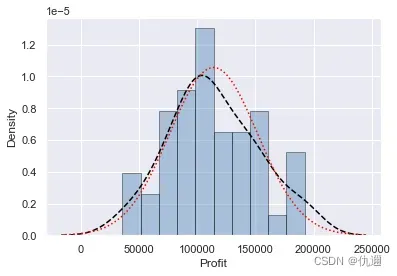
该图象绘制了Profit(因变量)的分布直方图,以及核密度曲线、正态核密度曲线。两个曲线越接近则说明该变量的分布越趋近于正态分布。
PP图与QQ图
import statsmodels.api as sm
X = Profit_New.Profit
pp_qq = sm.ProbPlot(X)
pp_qq.ppplot(line = '45')
plt.title('P-P figure')
pp_qq.qqplot(line = 'q')
plt.title('Q-Q figure')
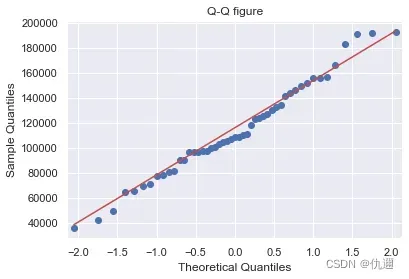
无论是 QQ图还是PP图,散点较为均匀地落在直线附近则说明数据基本服从正态分布。
Shapiro检验和K-S检验
两种方法均为非参数检验,原假设:变量服从正态分布。前者适合数据样本数量小于5000的数据;反之后者更加适用。
import scipy.stats as stats
## Shapiro
X = Profit_New.Profit
print('Shapiro检验结果:\n', stats.shapiro(X))
输出结果
Shapiro检验结果:
ShapiroResult(statistic=0.9793398380279541, pvalue=0.537902295589447)
解释:第一个数值为计算初的Shapiro检验的统计量;第二个数值为p值。p值 > 0.05,则接受原假设,即变量服从正态分布。
import numpy as np
rnorm = np.random.normal(loc = 5, scale = 2, size = 10000)
KS_Test1 = stats.kstest(rvs = rnorm, args = (rnorm.mean(), rnorm.std()), cdf = 'norm')
print('正态分布检验结果: \n', KS_Test1)
这里先是生成了10000个服从正态分布的随机数,正态分布检验必须规定args的数值,将均值和标准差进行传递。cdf参数规定了该检验是检验数据集的正态性。最终的结果p值 > 0.05表示接受原假设,数据呈正态分布。
多重共线性检验
多重共线性值的是自变量之间存在较高的线性相关关系,多存在多重共线性,会使得基于OLS算法拟合的回归模型失效,所以对其的检验至关重要。
方差膨胀因子VIF = 1 / (1 – R²),R²是从每个自变量与剩余变量的线性回归模型得出的判别系数。VIF > 10说明存在多重共线性; > 100则多重共线性非常严重。下面来看看如何通过python计算器多重共线性。若先是多重共线性过高,则可考虑lasso回归或岭回归。
from statsmodels.stats.outliers_influence import variance_inflation_factor
X = pd.concat([Profit.RD_Spend, Profit.Marketing_Spend], axis = 1)
vif = pd.DataFrame()
vif['Features'] = X.columns
vif["VIF_Factor"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
print(vif)
这里导入了statsmodels模块中提供计算VIF的函数。最终计算得到每个变量的VIF数值存储在VIF数据框中。
线性相关检验
线性相关的计算可通过Pearson线性关系进行分析,其目的就是为了验证自变量和因变量之间存在相关性。
corr = Profit_New.drop('Profit', axis = 1).corrwith(Profit_New.Profit)
print(corr)
输出结果:
RD_Spend 0.978437
Administration 0.205841
Marketing_Spend 0.739307
California -0.083258
Florida 0.088008
dtype: float64
先通过.drop函数去除Profit得到自变量数据,再利用corrwith()计算自变量与Profit之间的相关性。
一般来说,相关系数大于0.8为强相关;大于0.5为中度相关;大于0.3为弱相关;小于0.3几乎不相关。
import seaborn as sns
sns.pairplot(x)
这里我们调用由seaborn模块提供的绘制的三个变量与自变量之技安的散点图矩阵,结果如下:
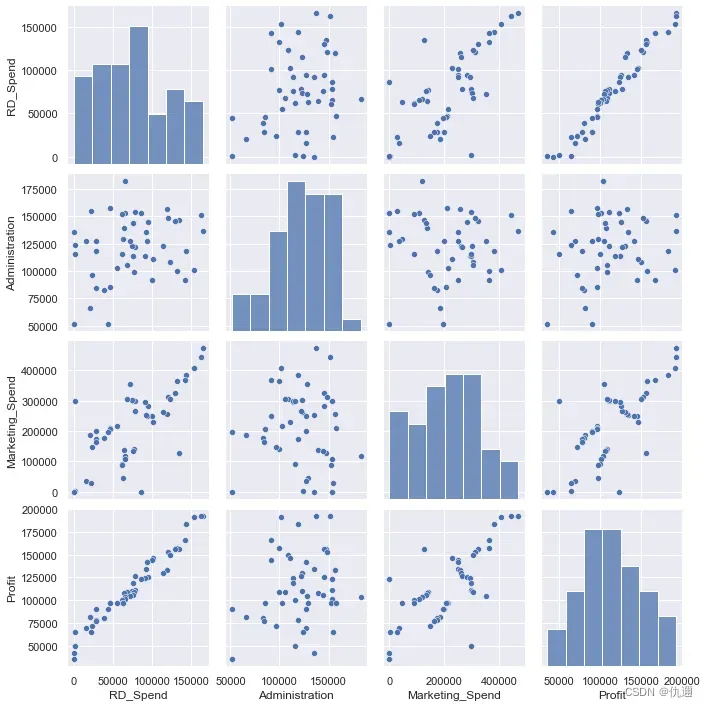
独立性检验
独立性检验可以通过模型的摘要中的DW统计量进行观察,其值若比较接近2则判定为该残差项具有独立性。
方差齐性
原假设:残杀的方差为一个常数,即不符合方差齐性。
BP检验
import statsmodels as sm
xx = sm.stats.diagnostic.het_breuschpagan(model.resid, exog_het=model.model.exog)
print(xx)
输出结果:
(3.3669127449599494, 0.6436139764746364, 0.6236233183413705, 0.6827863187824768)
输出结果中,第一个数值为LM统计量;第二个数值为概率p值,该值大于0.05则接受残差方差为常数的原假设;第三个值为F统计量,用于检验残差平方项与自变量之间是否独立,若独立则表明残差方差齐性;第四个值为F统计量的p值,同样大于0.05则进一步表示残差项满足方差齐性的假设。
文章出处登录后可见!
