在阅读本文之前,请确保您有一些基本的神经网络(可以先阅读西瓜书)。
本文采用的是标准BP算法,即每次仅针对一个样例更新权重和阈值。
本文将搭建用于分类的单隐层BP神经网络。
一、理论部分
1.1 正向计算
设我们的单隐层BP神经网络有个输入神经元,
个输出神经元,
个隐层神经元。
- 权重:第
输入神经元到第
隐藏层神经元的权重记为
,第
隐藏层神经元到
输出神经元的权重记为
;
- 阈值:第
隐藏层神经元的阈值记为
,第
输出神经元的阈值记为
;
- 输入:
输入神经元接收到的输入标记为
,
隐藏层神经元接收到的输入标记为
,
输出神经元接收到的输入标记为
;
- 输出:
隐藏层神经元的输出记为
,
输出神经元的输出记为
。
注,激活函数为
,我们定义:
注意,如果我们记得
然后有
再设,因此
。
类似地,是隐藏层和输出层之间的权重矩阵,我们有
再有。
所以我们得到了神经网络的输出。
1.2 反向传播
对于给定的训练样例,神经网络的输出为
,因此误差为
为了消除求导后多余的系数,我们做了一个过程,即令
我们采用梯度下降策略来最小化误差,即
在
让,可以知道
。另一方面
因此。
写出,
,得到权重和阈值的更新公式:
此外
在
让,然后我们得到
。另一方面
因此。
写出,
,得到权重和阈值的更新公式:
二、实现部分
2.1 算法伪码
这两个梯度项可以表示为:
其中代表逐元素操作。基于此,我们可以编写算法伪代码:
通过矩阵和向量化的表示,我们的单隐藏层神经网络可以简洁的表示成如下形式,也方便我们后续的编程。
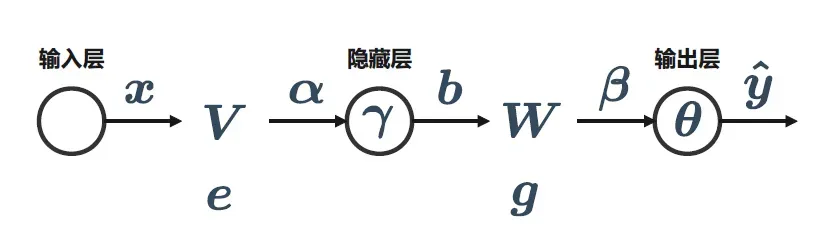
假设我们的激活函数采用Sigmoid函数,利用它的性质:,我们的两个梯度项变为:
2.2 算法实现
2.2.1 初始化
首先我们需要创建一个神经网络类:
import numpy as np
class NeuralNetwork:
def __init__(self):
pass
那么我们应该初始化哪些参数呢?输入层节点数、隐藏层节点数
和输出层节点数
必须初始化,它们决定了神经网络的结构。此外,根据算法伪代码,我们还应该初始化
。
注意必须手动输入,而权重矩阵和阈值向量由后三个参数决定。
当然,容忍度tol和 最大迭代次数max_iter也需要人工输入,这两个参数决定了我们的神经网络何时停止训练。
def __init__(
self,
learningrate,
inputnodes,
hiddennodes,
outputnodes,
tol,
max_iter
):
# 学习率
self.lr = learningrate
# 输入层结点数
self.ins = inputnodes
# 隐层结点数
self.hns = hiddennodes
# 输出层结点数
self.ons = outputnodes
# 容忍度
self.tol = tol
# 最大迭代次数
self.max_iter = max_iter
权重矩阵和阈值向量在范围内初始化:
# 权重矩阵和阈值向量
self.V = np.random.rand(self.hns, self.ins)
self.W = np.random.rand(self.ons, self.hns)
self.gamma = np.random.rand(self.hns)
self.theta = np.random.rand(self.ons)
当然,别忘了还有一个激活函数,我们以匿名函数的形式使用它:
# Sigmoid
self.sigmoid = lambda x: 1 / (1 + np.power(np.e, -x))
到此为止,我们的__init__()函数算是完成了:
def __init__(
self,
learningrate,
inputnodes,
hiddennodes,
outputnodes,
tol,
max_iter
):
self.lr = learningrate
self.ins, self.hns, self.ons = inputnodes, hiddennodes, outputnodes
self.tol = tol
self.max_iter = max_iter
self.V = np.random.rand(self.hns, self.ins)
self.W = np.random.rand(self.ons, self.hns)
self.gamma = np.random.rand(self.hns)
self.theta = np.random.rand(self.ons)
self.sigmoid = lambda x: 1 / (1 + np.power(np.e, -x))
2.2.2 正向传播
我们需要定义一个正向传播函数用来计算,该函数需要一个样本
作为输入,我们用(inputs, targets)来表示,输出
用outputs来表示。
当然,我们还需要计算误差,用error来表示。
def propagate(self, inputs, targets):
# 计算输入和输出
alpha = np.dot(self.V, inputs)
b = self.sigmoid(alpha - self.gamma)
beta = np.dot(self.W, b)
outputs = self.sigmoid(beta - self.theta)
# 计算误差
error = np.linalg.norm(targets - outputs, ord=2)**2 / 2
return alpha, b, beta, outputs, error
2.2.3 反向传播
反向传播需要先计算两个梯度项,然后进行参数更新:
可以看出我们的函数需要用到这些参数:。
def back_propagate(self, inputs, targets, alpha, b, beta, outputs):
# 计算两个梯度项
g = (targets - outputs) * outputs * (np.ones(len(outputs)) - outputs)
e = np.dot(self.W.T, g) * b * (np.ones(len(b)) - b)
# 更新参数
self.W += self.lr * np.outer(g, b)
self.theta += -self.lr * g
self.V += self.lr * np.outer(e, inputs)
self.gamma += -self.lr * e
2.2.3 训练
训练需要传入一个数据集,假设数据集的表示为(不知道这个表示法的读者可以参考我的这篇文章)。
我们需要对传入的数据集做一些处理。在遍历数据集时,X[i]是向量,即inputs,y[i]是向量对应的标签,它仅仅是一个数,而非像targets这样的向量。
那么如何将y[i]处理成targets呢?
考虑到像手写数字识别这样的第十类任务,相应的神经网络在输出层有十个神经元,每个神经元对应一个数字。例如,当我们输入的图片时,
对应的神经元的输出值应该是最高的,其他神经元的输出值应该是最低的。
因为激活函数是Sigmoid函数,它的输出区间为。我们将输出层神经元按照其对应的数字从小到大进行排列,从而输出层的情况应当十分接近下面这个样子:
y中包含了所有向量的标签,若要判断我们面临的问题是一个几分类问题,我们需要对y进行去重,再将结果从小到大进行排序:
self.classes = np.unique(y)
例如,y = [2, 0, 0, 1, 0, 1, 0, 2, 2],则self.classes = [0, 1, 2]。即self.classes中按序存储了所有的标签种类。
获得targets的步骤如下:
首先创建一个包含所有的数组,即
targets = np.zeros(len(self.classes))
然后我们要获取inputs的标签在self.classes中的索引,即
index = list(self.classes).index(y[i])
然后分配
targets[index] = 1
上述过程可以统一为两步:
targets = np.zeros(len(self.classes))
targets[list(self.classes).index(y[i])] = 1
我们之前提到,当且仅当满足以下两个条件之一时,训练才会停止:
- 迭代收敛,即
;
- 迭代次数达到最大值,即训练了max_iter次。
如果第一个条件先达到,则我们立刻停止训练;如果第二个条件先达到,说明我们训练了max_iter次也没有收敛,此时应当抛出一个错误。
def train(self, X, y):
# 初始时未收敛
convergence = False
self.classes = np.unique(y)
# 开始迭代 max_iter 次
for _ in range(self.max_iter):
# 遍历数据集
for idx in range(len(X)):
inputs, targets = X[idx], np.zeros(len(self.classes))
targets[list(self.classes).index(y[idx])] = 1
# 正向计算
alpha, b, beta, outputs, error = self.propagate(inputs, targets)
# 若误差不超过容忍度,则判定收敛
if error <= self.tol:
convergence = True
break
else:
# 反向传播
self.back_propagate(inputs, targets, alpha, b, beta, outputs)
if convergence:
break
if not convergence:
raise RuntimeError('神经网络的训练未收敛,请调大max_iter的值')
2.2.4 预测
训练好的神经网络理应能对单个样本完成分类,我们选择outputs中输出最高的神经元对应的类别标签作为我们对样本的预测标签:
def predict(self, sample):
alpha = np.dot(self.V, sample)
b = self.sigmoid(alpha - self.gamma)
beta = np.dot(self.W, b)
outputs = self.sigmoid(beta - self.theta)
# 计算输出最高的神经元在outputs中的索引
idx = list(outputs).index(max(outputs))
label = self.classes[idx]
return label
2.2.5 完善网络
至此,我们的神经网络就完成了,但是还有一些细节需要处理。
- 我们希望神经网络根据数据集自动调整输入层的节点数和输出层的节点数。
- 可以预设一些参数,例如学习率、容差等。
首先,我们需要修改__init__(),如下:
def __init__(self, X, y, hiddennodes, learningrate=0.01, tol=1e-3, max_iter=1000):
self.X, self.y = X, y
self.classes = np.unique(self.y)
self.ins, self.hns, self.ons = len(X[0]), hiddennodes, len(self.classes)
...
同时还需要修改一下train():
def train(self):
convergence = False
for _ in range(self.max_iter):
for idx in range(len(self.X)):
inputs, targets = self.X[idx], np.zeros(self.ons)
targets[list(self.classes).index(self.y[idx])] = 1
...
完整的单隐层神经网络代码如下:
import numpy as np
class NeuralNetwork:
def __init__(self, X, y, hiddennodes, learningrate=0.01, tol=1e-3, max_iter=1000):
self.X, self.y = X, y
self.classes = np.unique(self.y)
self.ins, self.hns, self.ons = len(X[0]), hiddennodes, len(self.classes)
self.lr = learningrate
self.tol = tol
self.max_iter = max_iter
self.V = np.random.rand(self.hns, self.ins)
self.W = np.random.rand(self.ons, self.hns)
self.gamma = np.random.rand(self.hns)
self.theta = np.random.rand(self.ons)
self.sigmoid = lambda x: 1 / (1 + np.power(np.e, -x))
def propagate(self, inputs, targets):
alpha = np.dot(self.V, inputs)
b = self.sigmoid(alpha - self.gamma)
beta = np.dot(self.W, b)
outputs = self.sigmoid(beta - self.theta)
error = np.linalg.norm(targets - outputs, ord=2)**2 / 2
return alpha, b, beta, outputs, error
def back_propagate(self, inputs, targets, alpha, b, beta, outputs):
g = (targets - outputs) * outputs * (np.ones(len(outputs)) - outputs)
e = np.dot(self.W.T, g) * b * (np.ones(len(b)) - b)
self.W += self.lr * np.outer(g, b)
self.theta += -self.lr * g
self.V += self.lr * np.outer(e, inputs)
self.gamma += -self.lr * e
def train(self):
convergence = False
for _ in range(self.max_iter):
for idx in range(len(self.X)):
inputs, targets = self.X[idx], np.zeros(self.ons)
targets[list(self.classes).index(self.y[idx])] = 1
alpha, b, beta, outputs, error = self.propagate(inputs, targets)
if error <= self.tol:
convergence = True
break
else:
self.back_propagate(inputs, targets, alpha, b, beta, outputs)
if convergence:
break
if not convergence:
raise RuntimeError('神经网络的训练未收敛,请调大max_iter的值')
def predict(self, sample):
alpha = np.dot(self.V, sample)
b = self.sigmoid(alpha - self.gamma)
beta = np.dot(self.W, b)
outputs = self.sigmoid(beta - self.theta)
return self.classes[list(outputs).index(max(outputs))]
我们将其保存到nn.py中。
3. 实践培训
本章节中,我们使用sklearn中的鸢尾花数据集来训练并测试神经网络。
另起一个新的.py文件,首先需要导入:
from nn import NeuralNetwork # 导入我们的神经网络
from sklearn.model_selection import train_test_split # 划分训练集和测试集
from sklearn.metrics import accuracy_score # 计算分类准确率
from sklearn.datasets import load_iris # 鸢尾花数据集
from sklearn.preprocessing import MinMaxScaler # 数据预处理
import numpy as np
先做数据预处理:
X, y = load_iris(return_X_y=True)
scaler = MinMaxScaler().fit(X)
X_scaled = scaler.transform(X)
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)
创建一个神经网络实例,将隐藏层结点数设为 10,然后进行训练:
bpnn = NeuralNetwork(X_train, y_train, 10, max_iter=3000) # max_iter过小会导致不收敛
bpnn.train()
定义一个函数来计算神经网络在测试集上的分类精度:
def test(bpnn, X_test, y_test):
y_pred = [bpnn.predict(X_test[i]) for i in range(len(X_test))]
return accuracy_score(y_test, y_pred)
print(test(bpnn, X_test, y_test))
# 1.0
可以看出,训练好的神经网络在测试集上的分类准确率为。
完整的训练/测试代码如下:
from nn import NeuralNetwork
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.datasets import load_iris
from sklearn.preprocessing import MinMaxScaler
import numpy as np
def test(bpnn, X_test, y_test):
y_pred = [bpnn.predict(X_test[i]) for i in range(len(X_test))]
return accuracy_score(y_test, y_pred)
X, y = load_iris(return_X_y=True)
scaler = MinMaxScaler().fit(X)
X_scaled = scaler.transform(X)
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)
bpnn = NeuralNetwork(X_train, y_train, 10, max_iter=3000)
bpnn.train()
print(test(bpnn, X_test, y_test))
版权声明:本文为博主serity原创文章,版权归属原作者,如果侵权,请联系我们删除!
原文链接:https://blog.csdn.net/weixin_44022472/article/details/123315557
