网上关于机器学习算法的讲解很多,不过推导过程可能比较繁琐,结论比较隐蔽。为了能够让c/c++的初学者通过代码简单的实现、加深理解,所以本文章简单的总结出结论,尽量减少推导过程。并且将各个变量的范围、意义做出解释。
我目前大学本科在读,非人工智能专业,第一次接触机器学习,本文章仅是我的学习记录和总结,所有的处理方式都不一定是最正确的。但是致力于让只学完c\c++基本语法的人也能实现该算法。
如果您不知道如何处理数据并获取“输入”,请阅读我的文章:《机器学习数据的预处理》(如果找不到说明,我还没有写)。
另外,我会尽可能多打括号,防止各位对到底对什么求和感到困惑,变量也用x[a]而非
表示,便于直接写成代码。
第一的:
算法的输入可以是连续的。另外,根据我的几次实践,“归一化”或“归一化”的学习结果根据初始化方法的不同而不同,结果都很好,但是直接使用原始数据时结果很差。
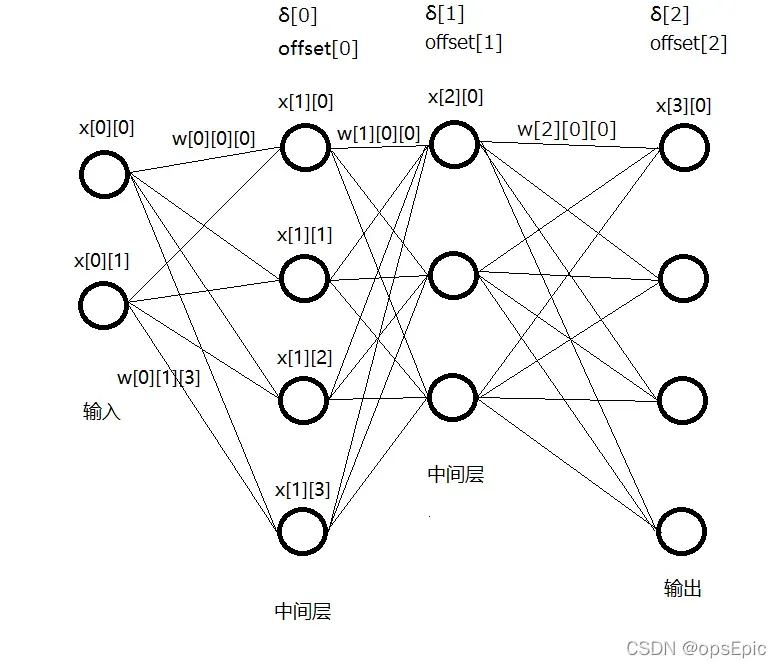
图中有些变量标注了,有些需要的变量没有标注。所有变量的含义如下:
1. x[a][b],表示第a层第b个神经元的取值。是浮点型
2. w[a][b][c],表示x[a][b]输出传递到x[a+1][c]的权重。是浮点型(具体下方再讲)
3. offset[a],表示第a+1层的每个x得到输入后,需要加的偏移值。是浮点型(具体下方再讲)
4. δ[a],是期望与实际输出比较,来更新w与offset时,所引入的中间变量。是浮点型(具体下方再讲)
5. n[a](图中未标出),是第a层x的个数,每层的x个数可以不同。显然是整型
6. e[a](图中未标出),是输出层即最后一层的期望值,根据我给出的公式e∈(0,1)。是浮点型
7. η(图中未标出),是更新w与offset时得到更新量需乘的∈(0,1)的小数。是浮点型(具体下方再讲)
计算输出和更新w与offset:
1. 计算得到输出:正向,输入层的x直接拷贝数据预处理得到的“输入”,然后先计算第1层按顺序一直计算到输出层,每个
在
(g(x)也可以不为该式,但是下面δ的计算会发生改变)
有些文章中,有且仅有输出层不通过x=g()的计算,直接将g()括号中的值作为输出,那样可能输出层δ的计算公式要发生变化,而且输出的数据将∈(0,+∞),而通过x=g()的计算后,输出的数据∈(1,0)。实际上,我认为输出数据的范围意义不大,可以有多种方法来理解输出的值,具体下方再讲
如果已经训练结束,则只需要得到输出,不需要计算δ,也不需要更新w与offset。
2. 计算得到δ:反向,先计算输出层按顺序一直计算到第1层(输入层是第0层,图中也可以看到,输入层没有对应的δ),输出层的
(因为是计算输出层,该式中显然:a=总层数-1)
非输出层,每个
3. 更新w与offset:正向,先更新第1层的w与offset,按顺序更新到输出层,每个
(注意“-=”不是“=”)
每个
(注意“-=”不是“=”)
初始化:
初始化为什么放在计算公式之后讲呢,因为各位通过计算公式可以很明确的看出,所有的x都是过程量,保存了w与offset即保存了该算法的学习结果。也就是说,做初始化就是对w与offset做初始化。同样的,保存w与offset即保存了该学习算法的学习结果。
显然w与offset全部初始化为0是不行的,这里介绍我最常使用的Xavier initialization初始化方法,即保证每一层输出的方差相等,每个:
c/c++如何实现正态分布的代码这里不再多做介绍。如果实在找不到,或写不出来可以简单的采用∈(-1,1)的均匀分布。
对期望和输出值的理解:
对输入的理解请看《机器学习数据的预处理》(如果找不到说明,我还没写)。
一些简单的用途中,输出层x的个数可以仅为1,用于解决二分问题。例如,输出∈(0,0.5)表示“否”,∈【0.5,1)表示“是”,则期望(即e)可以为0.9或0.1(e∈(0,1)不应为0或1,具体下方再讲)
另外的情况下,输出层x的个数大于1,可以取值最大的一个x为答案,也可以取最大的几个x,判断正确答案是否在其中。
如果还是不能理解取最大x的意义,可以看下面的例子:
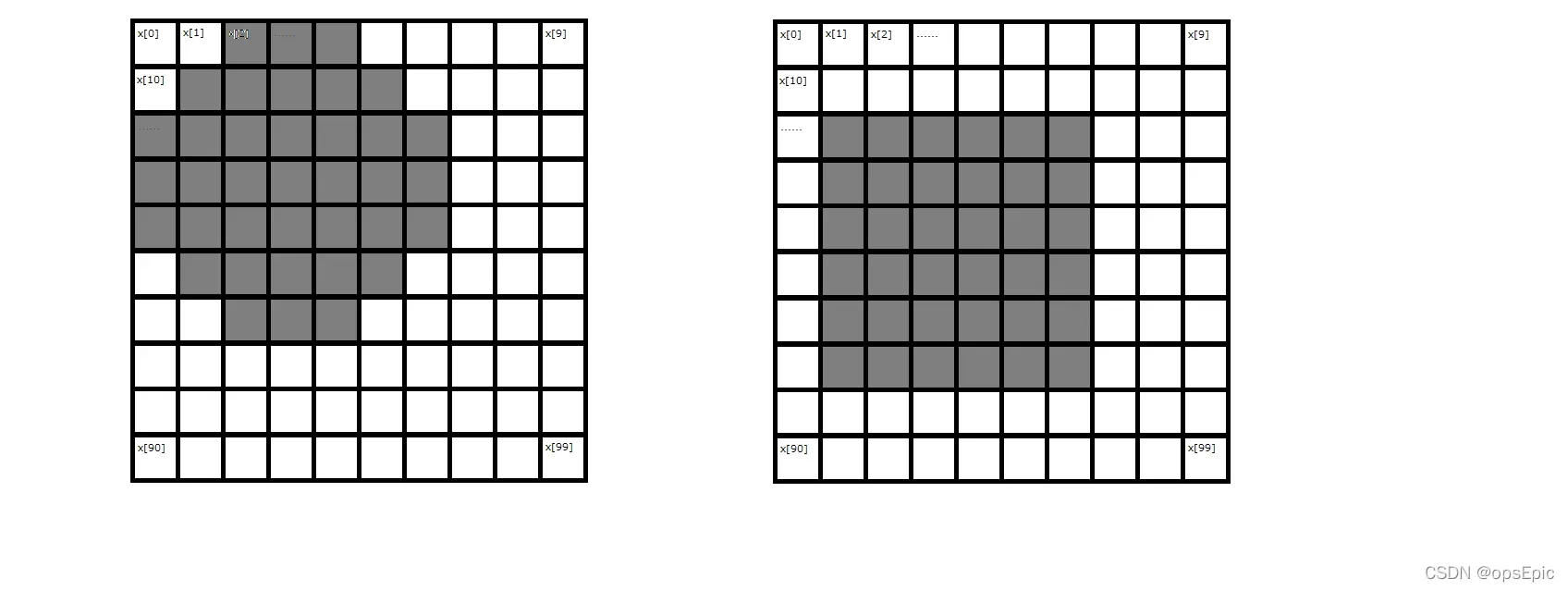
这是一个10*10的二维数组,实际上就是长度为100的一维数组,用代码随机生成圆形或方型,显然,输入层x的数量为100,若输出层数量为2,且使上图所示涂黑部分对应输入层x值为1,否则为0,是圆形时e[0]=0.1,e[1]=0.9,是方形时e[0]=0.9,e[1]=0.1,经过学习(即w与offset的更新),再次输入圆形时,e[1]大概率会大于e[0],反之,e[0]大概率会大于e[1],那么是否可以说e[1]表示圆形,e[0]表示方形?当然还可以再增加输出层x的数量用于表示三角形等其他更多图形。
您可能会遇到的一些问题:
1. 关于η的取值,η=1的不同情况:
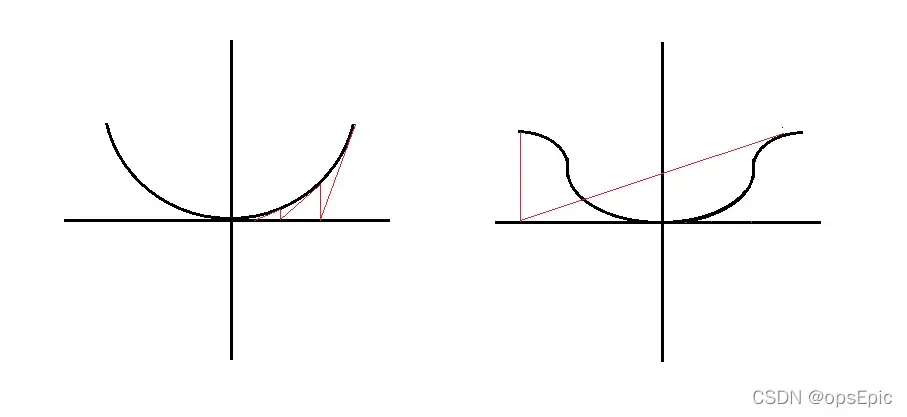
图是windows自带画图软件画的,比较丑陋,但是很显然,η的取值会影响学习的成功与否,如果学习失败可以尝试减小η的取值。
2. e的取值
如果e=1,只看输出层,x会无限趋近1,则g()括号中的数值会趋于+∞,结果可能会使w与offset趋于无限大。另外,一些其他原因也会导致这种情况,在检查自己的算法正确后,试着改变η的取值,其它能造成该问题的原因我暂时还没有遇到。
3. 层数及每层x数量的选择
一般情况下层数不需要很多,我在做NSL-KDD的训练之时就发现:隐藏层层数仅1层即可达到较高的正确率,而且在输入层x数量非常大的情况下,如果隐藏层x数量同样大将会使计算速度非常缓慢,另外,更多的层数将需要更多的样本来学习。
最后:
写的很匆忙,很多地方都没有查。我学习这些算法的时间也很短。如有问题,欢迎提出意见或建议,我会第一时间更正。
此外,要深入理解一个算法,还需要学习它的具体原理和推导过程。网上关于这个话题的文章太多了,这里就不详细解释了。
谢谢。
文章出处登录后可见!
