1 信息熵(Information entropy)

熵 (Entropy)，信息熵(Information entropy)：常被用来作为一个系统的信息含量的量化指标，从而可以进一步用来作为系统方程优化的目标或者参数选择的判据。

1.1 信息熵(Information entropy)的性质

• 单调性，发生概率越高，携带的信息量越少；
  
• 非负性，信息熵(Information entropy)可以看作是一个广义(Lagrangian generalized Lagrangian)的度量，非负性是合理的必要性；
  
• 可加性，多个随机事件同时发生的总不确定性(deterministic)的度量近似等于每个事件的不确定性(deterministic)度量的总和，
  
• 假设(Hypothesis)信息熵(Information entropy)的函数是I，计算概率的函数是P，I是关于P的减函数，即I(P1,P2)=I(P1)+I(P2)。
  

1.1.1 信息熵(Information entropy)的公式

Shannon 在数学上严格证明，满足上述三个条件的随机变量(random variable)不确定性(deterministic)测量函数具有唯一形式：

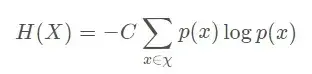
其中的 C 为常数，我们将其归一化(Normalization)为 C = 1 C=1C=1 即得到了信息熵(Information entropy)公式。目前，信息熵(Information entropy)大多都是通过上式进行计算的（式中的Pi是概率函数Pi(Ui）的计算结果，求和符号(symbol)中的i代表从1到n之间的整数。在实践中对数一般以2为底，约定0log0=0。

1.2 信息熵(Information entropy)的计算公式

信息熵(Information entropy)是一个抽象概念，其计算方法没有固定的公式。任何符合信息熵(Information entropy)特性的公式都可以用于信息熵(Information entropy)的计算。

1.2.1 对数的信息熵(Information entropy)

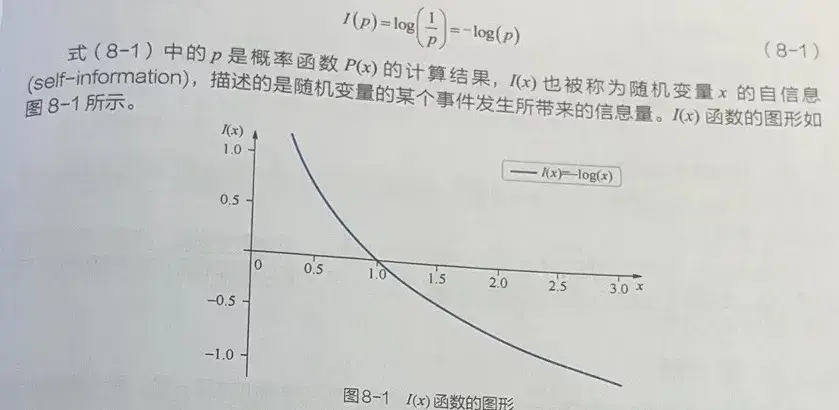
1.2.2 单符号(symbol)二元信源的信息熵(Information entropy)

以一个最简单的单符号(symbol)二元信源为例说明，该信源符号(symbol)U(上式中的X)仅可以取值为a或b。其中，取a的概率为p，则取b的概率为1-p。该信源的信息熵(Information entropy)可以记为H(U)=pI(p)+(1-p)I(1-p)，所形成的曲线如图所示。

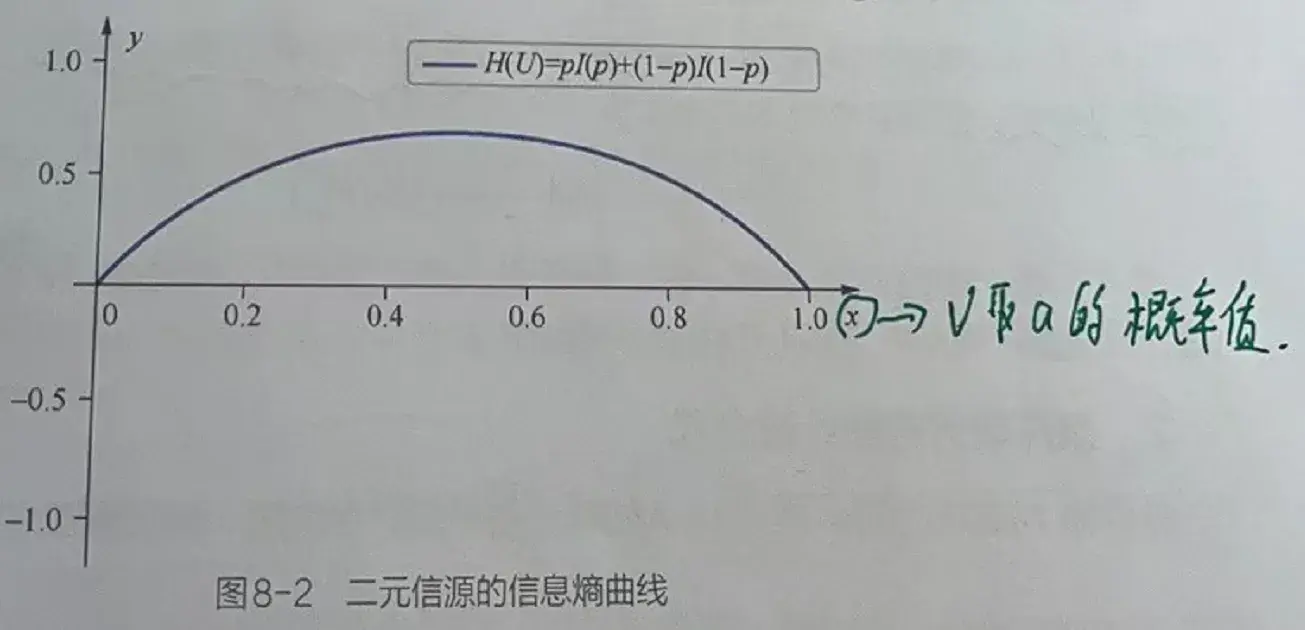
在图8-2中，x轴代表符号(symbol)U取值为a的概率值p，y轴代表符号(symbol)U的信息熵(Information entropy)H(U)。由图8-2可以看出信息熵(Information entropy)有如下几个特性。

• 确定性(deterministic)：当符号(symbol)U取值为a的概率值p=0和p=1时，U的值是确定的，没有任何变化量，所以信息熵(Information entropy)为0。
  
• 极值性：当p=0.5时，U的信息熵(Information entropy)达到了最大。
  
• 对称性：图形在水平方向关于p=0.5对称。
  
• 非负性：即收到一个信源符号(symbol)所获得的信息熵(Information entropy)应为正值，H(U)≥0。
  

1.3 连续信息熵(Information entropy)及特性

源中的变量从连续数据中取值。一个连续的源可以有无限的值，信息量是无限的，所以计算信息熵(Information entropy)是没有意义的。一般采用其他连续源作为参考来衡量相对熵值。

1.4 联合熵

联合熵(joint entropy)可将一维随机变量(random variable)分布(Distribution)推广到多维随机变量(random variable)分布(Distribution)。两个变量x和Y的联合信息熵(Information entropy)H(X,Y)也可以由联合概率函数P(x,y)计算得来：

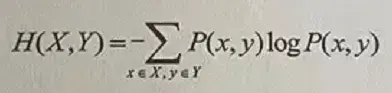
式中的联合概率函数P(x,y)是指x、y同时满足某一条件的概率。

1.5 条件熵(Conditional entropy)

条件熵(Conditional entropy)(conditional entropy)表示在已知随机变量(random variable)X的条件下，随机变量(random variable)Y的不确定性(deterministic)，条件熵(Conditional entropy)H(Y|X)可以由联合橱率函数P(x,y)和条件概率(conditional probability)函数P(y|x)计算得来：

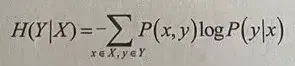
其中 P(x,y)=P(y|x)P(x)，即x和y的联合概率等于“在x条件下，y出现的概率”乘以“x的边际概率”。

1.5.1 条件熵(Conditional entropy)的另一种计算方式

条件熵(Conditional entropy)H(Y|X)也可以由X和Y的联合信息熵(Information entropy)计算而来：

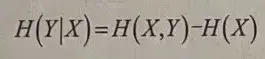
可以描述为，条件熵(Conditional entropy)H(Y|X)等于联合熵H(X,Y)减去X的边际熵H(X)。

1.6 交叉熵(Cross entropy)

交叉熵(Cross entropy)(cross entropy)在神经网络中常用于计算分类模型的损失。交叉熵(Cross entropy)表示的是实际输出（概率）与期望输出（概率）之间的距离。交又熵越小，两个概率越接近。

1.6.1 交叉熵(Cross entropy)数学公式

交叉熵(Cross entropy)公式假设(Hypothesis)样本集的概率分布(probability distribution)(Distribution)函数为P(x)，模型预测结果的概率分布(probability distribution)(Distribution)函数为Q(x)，则真实样本集的信息熵(Information entropy)为（p是函数P(x)的值)：

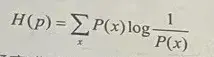
使用模型预测结果的概率分布(probability distribution)(Distribution)Q(x)来表示数据集(Dataset)中样本分类的信息熵(Information entropy)，则上述式子可改写为：

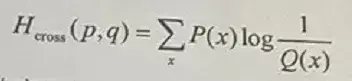
Q(x)与P(x)的交叉熵(Cross entropy)。因为分类的概率来自样本集，所以式中的概率部分用Qx)来表示。

1.6.2 交叉熵(Cross entropy)损失

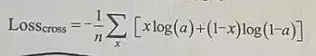
交叉熵(Cross entropy)损失表示模型对正向样本预测的交叉熵(Cross entropy)（求和项中的第一项)与对负向样本预测的交叉熵(Cross entropy)（求和项中的第二项）之和。正向样本的概率为a，预测负向样本的概率为1-a。

1.7 相对熵/KL散度(KLdivergence)(Divergence)/信息散度(Divergence)

相对熵，又被称为KL散度(KLdivergence)(Divergence)或信息散度(Divergence)，用来度量两个概率分布(probability distribution)(Distribution)间的非对称性差异。在信息理论中，相对熵等价于两个概率分布(probability distribution)(Distribution)的信息熵(Information entropy)的差值。

1.7.1 相对熵的公式

设P(x)、Q(x)是离散随机变量(random variable)集合X中取值x的两个概率分布(probability distribution)(Distribution)函数，它们的结果分别为p和q，则p对q的相对熵如下：

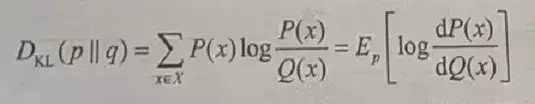
由式可知，当P(x)和Q(x)两个概率分布(probability distribution)(Distribution)函数相同时，相对熵为0（因为log1=0）并且相对熵具有不对称性，“Ep”代表期望,期望是指每次可能结果的概率乘以结果的总和。

1.7.2 相对熵与交叉熵(Cross entropy)的关系

将1.7.1中式子中对数部分展开，可以看到相对熵与交叉熵(Cross entropy)之间的关系：

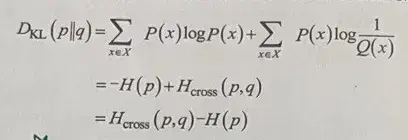
由式可以看出p与q的相对熵是由二者的交叉熵(Cross entropy)去掉p的边际熵得来，相对熵是交叉熵(Cross entropy)中去掉熵的部分。

在神经网络中，由于训练数据集(Dataset)是固定的，即p的嫡一定，因此最小化交叉熵(Cross entropy)等价于最小化预测结果与真实分布(Distribution)之间的相对熵（模型的输出分布(Distribution)与真实分布(Distribution)的相对熵越小，表明模型对真实样本拟合效果越好)，这也是要用交叉熵(Cross entropy)作为损失函数(Loss function)的原因。

1.8 JS散度(Divergence)

1.8.1 JS散度(Divergence)出现的原因

KL散度(KLdivergence)(Divergence)可以表示两个概率分布(probability distribution)(Distribution)的差异，但它并不是对称的。在使用KL散度(KLdivergence)(Divergence)训练神经网络时，会有因顺序不同而造成训川练结果不同的情况。

1.8.2 JS散度(Divergence)

JS散度(Divergence)在KL散度(KLdivergence)(Divergence)的基础上进行了一次变换，使两个概率分布(probability distribution)(Distribution)(p、q)间的差异度量具有对称性：

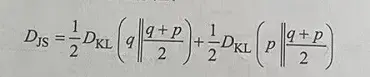
1.8.3 JS散度(Divergence)的特性

与KL散度(KLdivergence)(Divergence)相比，JS散废更适合在神经网络中应用。它具有以下特性。

• 对称性：可以衡量两个不同分布(Distribution)之间的差异。
  
• 大于或等于0：当两个分布(Distribution)完全重叠时，其JS散度(Divergence)达到最小值0。
  
• 有上界：当两个分布(Distribution)差异越来越大时，其JS散度(Divergence)的值会逐渐增大。当两个分布(Distribution)的JS散度(Divergence)足够大时，其值会收敛(Convergence)到一个固定值，KL散度(KLdivergence)(Divergence)是没有上界的。
  
• 在互信息(Mutual information)的最大化任务中，常使用JS散度(Divergence)来代替KL散度(KLdivergence)(Divergence)。
  

2 互信息(Mutual information)

互信息(Mutual information)是衡量随机变量(random variable)之间相互依赖(dependency)程度的指标，用来衡量两个变量之间共享的信息量。

2.1 三句话解释互信息(Mutual information)

• 一个随机变量(random variable)中包含的关于另一个随机变量(random variable)的信息量，
  
• 由于另一个已知随机变量(random variable)的变化而降低了随机变量(random variable)的不确定性(deterministic)。
  
• 例如，中午去吃饭的不确定性(deterministic)和随时去吃饭的不确定性(deterministic)之间的差异。
  

2.2 互信息(Mutual information)公式

设有两个变量集合X和Y，它们中的个体分别为x、y，它们的联合概率分布(probability distribution)(joint probability distribution)(Distribution)函数为P(x,y)，边际概率分布(probability distribution)(Distribution)函数分别是P(x)、P(y)。互信息(Mutual information)是指联合概率分布(probability distribution)(joint probability distribution)(Distribution)函数P(x,y)与边际概分布(Distribution)函数P(x),P(y)的相对熵。

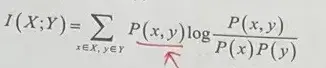
2.3 互信息(Mutual information)的特点

(1)对称性：由于互信息(Mutual information)属于两个变量间的共享信息，因此I(X;Y)=I(Y|X)。
(2)独立变量间互信息(Mutual information)为0：如果两个变量独立，则它们之间没有任何共享信息，此时互信息(Mutual information)为0。
(3)非负性：共享信息要么有，要么没有。互信息(Mutual information)量不会出现负值。

2.4 互信息(Mutual information)与条件熵(Conditional entropy)之间关系

2.5 互信息(Mutual information)与联合熵之间关系

2.6 互信息(Mutual information)的应用

• 互信息(Mutual information)已被用作机器学习(machine learning)中特征选择(Feature selection)和特征转换的标准。它可以表示变量的相关性和冗余性，例如最少冗余的特征选择(Feature selection)。它可以确定数据集(Dataset)中两个不同聚类(Clustering)的相似性。
  
• 也可用于时间序列分析中的相位同步目标检测。
  
• 对抗神经网络（如DIM模型）及图神经网络（如DGI模型）中，使用互信息(Mutual information)来作为无监督方式提取特征的方法。