吴恩达机器学习作业8 – 异常检测和推荐系统（Python实现）

Introduction

在第一个实验中，将实施异常检测算法并将其应用于检测网络上的故障服务器。在第二个实验中，我们将使用协同过滤来构建电影推荐系统。

1 Anomaly detection（异常检测）

在本实验中，将实施异常检测算法来检测服务器计算机中的异常行为。特征测量每个服务器的响应速度（mb/s）和延迟（ms）。在服务器运行时，收集计算机行为的样本，因此有一个未标记的数据集，其中绝大多数样本是正常的，但仍有一小部分样本是异常的。

使用高斯模型检测数据集中的异常样本，从2D数据集开始可视化运行的算法。在这个数据集上，拟合一个高斯分布，然后找一个概率比较低的值，以此为标准，较低的值被认为是异常。泛化：将异常检测算法应用于多维数据集。

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.io import loadmat

data=loadmat("./data/ex8data1.mat")
data.keys()

dict_keys(['__header__', '__version__', '__globals__', 'X', 'Xval', 'yval'])

X=data['X']
Xval,yval=data['Xval'],data['yval']
X.shape,Xval.shape,yval.shape

((307, 2), (307, 2), (307, 1))

def plot_data(X):
    plt.figure(figsize=(8,6))
    plt.plot(X[:,0],X[:,1],'x',color="blue")
    plt.xlabel("Latency (ms)")
    plt.ylabel("Throughput (mb/s)")
    plt.title("The first dataset")

plot_data(X)

​​​

​​​

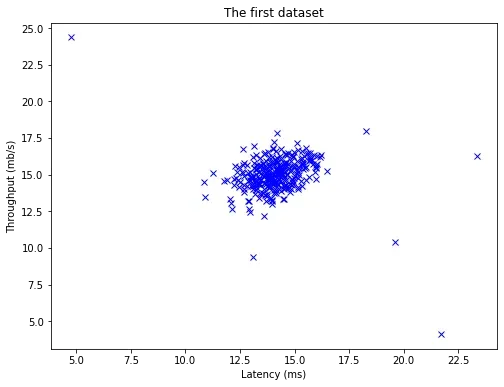
1.1 Gaussian distribution（高斯分布）

要执行异常检测，您首先需要将数据的分布拟合到模型中。给定一个训练集，估计每个特征的高斯分布并找到来拟合数据。

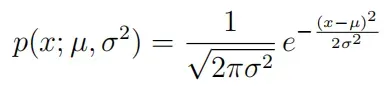
其中是均值，控制方差。

1.2 Estimating parameters for a Gaussian（高斯分布的参数估计）

估计参数：

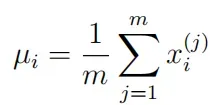
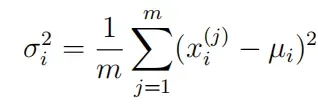
写函数estimateGaussian：以数据矩阵X为输入，输出一个维向量（包含特征的均值）和另一个维向量（包含特征的方差）。

完成上述函数的编写后，将拟合后的高斯分布的轮廓可视化，可以看到大部分样本在概率最高的区域，而异常样本在概率较低的区域。

def estimateGaussian(X):
    mu=X.mean(axis=0)
    sigma=X.var(axis=0)
    return mu,sigma

mu,sigma=estimateGaussian(X)
mu,sigma

(array([14.11222578, 14.99771051]), array([1.83263141, 1.70974533]))

用参数计算高斯分布模型中每个样本的概率值：

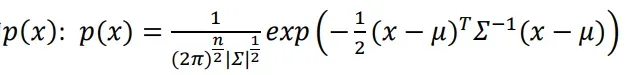
def gaussian(X,mu,sigma):
    #X:(m,n)
    m,n=X.shape
    if(np.ndim(sigma)==1):
        sigma=np.diag(sigma)
    left=1.0/(np.power(2*np.pi,n/2)*np.sqrt(np.linalg.det(sigma)))
    right=np.zeros((m,1))
    for row in range(m):
        x=X[row]
        right[row]=np.exp(-0.5*(x-mu).T@np.linalg.inv(sigma)@(x-mu))
    return left*right

# xplot = np.linspace(0, 25, 100)  # 分割为m=100份
# yplot = np.linspace(0, 25, 100)  # 分割为n=100份
# Xplot, Yplot = np.meshgrid(xplot, yplot)  # 生成n*m的矩阵
# points=np.c_[Xplot.flatten(),Yplot.flatten()]
# Z = gaussian(points, mu, sigma).reshape(Xplot.shape)
# contour = ax.contour(Xplot, Yplot, Z, [10**-11, 10**-7, 10**-5, 10**-3, 0.1], colors='k')  # 绘制等高线
# ax.plot(X[:, 0], X[:, 1], 'x', color="blue")
# ax.set_xlabel("Latency (ms)")
# ax.set_ylabel("Throughput (mb/s)")
# ax.set_title(" The Gaussian distribution contours of the distribution fit to the dataset")
# plt.show()

可视化数据：

def plotContours(fig=None,ax=None):#用于绘制等高线
    xplot=np.linspace(0,25,100)#分割为m=100份
    yplot=np.linspace(0,25,100)#分割为n=100份
    Xplot,Yplot=np.meshgrid(xplot,yplot)#生成n*m的矩阵
    # Z=np.exp(-0.5*(np.power(Xplot-mu[0],2)/sigma[0]+np.power(Yplot-mu[1],2)/sigma[1]))
    Z = gaussian(points, mu, sigma).reshape(Xplot.shape)
    contour=ax.contour(Xplot, Yplot, Z,[10**-11, 10**-7, 10**-5, 10**-3, 0.1],colors='k')#绘制等高线
    ax.plot(X[:,0],X[:,1],'x',color="blue")
    ax.set_xlabel("Latency (ms)")
    ax.set_ylabel("Throughput (mb/s)")
    ax.set_title(" The Gaussian distribution contours of the distribution fit to the dataset")
    # plt.show()

# plt.figure(figsize=(8,6))
fig,ax=plt.subplots(figsize=(8,6))
plotContours(fig,ax)
plt.show()

​​​

​​​

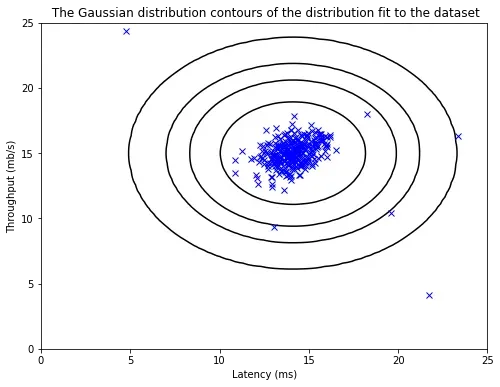
从上图中可以清楚地看出，哪些样本概率高，哪些样本概率低，而概率低的样本很大程度上是异常值。

1.3 Selecting the threshold（选择阈值）

既然已经估计了高斯参数，就可以研究在给定分布下哪些样本的概率非常高，哪些样本的概率非常低。概率低的样本更有可能是数据集中的异常值。确定哪些样本是异常值可以考虑根据交叉验证集选择一个阈值。在这部分实验中，将实现一种算法，该算法使用交叉验证集上的分数来选择阈值。

写函数selectThreshold：使用交叉验证集（其中对应异常样本，对应正常样本）。对于每个交叉验证样本，计算。概率向量作为参数pval传递给函数selectThreshold，标签作为参数yval传递给函数selectThreshold。函数selectThreshold返回两个参数：阈值（样本x的概率，则认为是异常），分数（在阈值下找到真正异常的好坏）

使用prec和rec计算分数：

还有、

• tp：本身是异常值并且模型预测成异常值，即真的异常值
  
• fp：本身是正常值并且模型预测成异常值，即假的异常值
  
• fn：本身是异常值并且模型预测成正常值，即假的正常值
  
• precision：表示预测为异常值的样本中有多少是真的异常值的样本
  
• recall：表示实际为异常值的样本中有多少成功预测出是异常值
  

使用SciPy的内置方法stats：计算一个数据点属于正态分布的概率：

from scipy import  stats
dist=stats.norm(mu[0],sigma[0])
dist.pdf(15)

0.1935875044615038

将数组传递给概率密度函数，得到数据集中每个点的概率密度：

dist.pdf(X[:,0])[0:10]

array([0.183842  , 0.20221694, 0.21746136, 0.19778763, 0.20858956,
       0.21652359, 0.16991291, 0.15123542, 0.1163989 , 0.1594734 ])

计算并保存上述高斯模型参数数据集中每个值的概率密度：

p=np.zeros((X.shape))
p[:,0]=stats.norm(mu[0],sigma[0]).pdf(X[:,0])
p[:,1]=stats.norm(mu[1],sigma[1]).pdf(X[:,1])
p.shape

(307, 2)

计算并保存上述高斯模型参数验证集中每个值的概率密度：

pval=np.zeros((Xval.shape))
pval[:,0]=stats.norm(mu[0],sigma[0]).pdf(Xval[:,0])
pval[:,1]=stats.norm(mu[1],sigma[1]).pdf(Xval[:,1])
pval.shape

(307, 2)

写一个函数selectThreshold：计算的不同值的分数（是真阳性、假阳性和假阴性数量的函数），找到给定概率密度值和真标签的最佳阈值。如果你运行给定的数据集，你得到的最好的 大约是 。

def selectThreshold(pval,yval):
    best_e,best_f1,f1=0,0,0
    step=(pval.max()-pval.min())/1000
    for e in np.arange(pval.min(),pval.max(),step):
        preds=pval<e
        tp=np.sum(np.logical_and(preds==1,yval==1))
        fp=np.sum(np.logical_and(preds==1,yval==0))
        fn=np.sum(np.logical_and(preds==0,yval==1))
        precision=tp/(tp+fp)
        recall=tp/(tp+fn)
        f1=(2*precision*recall)/(precision+recall)
        if(f1>best_f1):
            best_f1=f1
            best_e=e
    return best_e,best_f1

epsilon, f1 = selectThreshold(pval, yval)
epsilon, f1

<ipython-input-92-c5a1372ada03>:9: RuntimeWarning: invalid value encountered in long_scalars
  precision=tp/(tp+fp)





(0.009566706005956842, 0.7142857142857143)

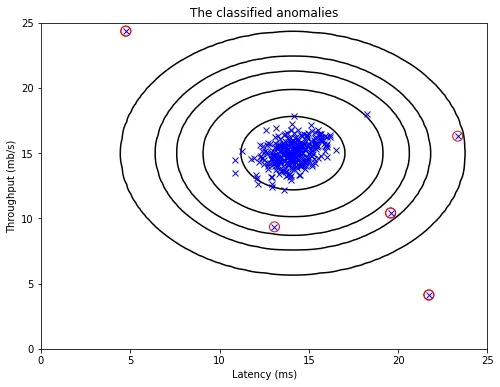
将得到的最佳阈值应用于数据集并可视化结果：

先看预测的异常样本：第一个数组是异常样本编号，第二个数组是异常样本对应的。

out_index=np.where(p<epsilon)
out_index

(array([300, 301, 301, 303, 303, 304, 306, 306], dtype=int64),
 array([1, 0, 1, 0, 1, 0, 0, 1], dtype=int64))

下图中的红点是标注为异常样本的点，但也有一些异常样本（但没有标注），比如右上角也可能是异常样本。找到的最好的和画出来的图都不理想。接下来换个方法求解：使用前面的函数gaussian求解样本的概率，而不是直接使用scipy的库函数。

fig,ax=plt.subplots(figsize=(8,6))
plotContours(fig,ax)
plt.xlabel("Latency (ms)")
plt.ylabel("Throughput (mb/s)")
plt.title("The classified anomalies")
plt.scatter(X[out_index[0],0],X[out_index[0],1],s=100,facecolors="none",edgecolors="r")
plt.show()

​​​

​​​

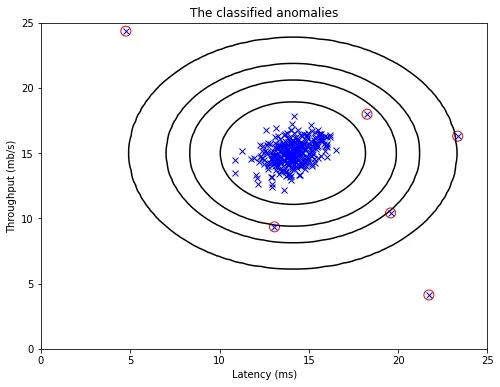
下面解出的最好的满足要求，绘制的图形也比较理想。

p = gaussian(X, mu, sigma)
pval = gaussian(Xval, mu, sigma)
epsilon, f1 = selectThreshold(pval, yval)
epsilon, f1

<ipython-input-92-c5a1372ada03>:9: RuntimeWarning: invalid value encountered in long_scalars
  precision=tp/(tp+fp)





(8.990852779269496e-05, 0.8750000000000001)

out_index=np.where(p<epsilon)
out_index

(array([300, 301, 303, 304, 305, 306], dtype=int64),
 array([0, 0, 0, 0, 0, 0], dtype=int64))

fig,ax=plt.subplots(figsize=(8,6))
plotContours(fig,ax)
plt.xlabel("Latency (ms)")
plt.ylabel("Throughput (mb/s)")
plt.title("The classified anomalies")
plt.scatter(X[out_index[0],0],X[out_index[0],1],s=100,facecolors="none",edgecolors="r")
plt.show()

​​​

​​​

1.4 High dimensional dataset

在本节实验的数据集中，每个样本都有特征，其中包含了计算服务器的更多属性。使用上面的代码估计高斯参数，并根据这些参数评估数据集X和交叉验证集Xval中样本的概率。最后利用函数selectThreshold找到最佳阈值，最佳约为，找到异常样本。

data2=loadmat("./data/ex8data2.mat")
X2=data2['X']
Xval2,yval2=data2['Xval'],data2['yval']
X2.shape,Xval2.shape,yval2.shape

((1000, 11), (100, 11), (100, 1))

mu,sigma=estimateGaussian(X2)
p = gaussian(X2, mu, sigma)
pval = gaussian(Xval2, mu, sigma)
epsilon, f1 = selectThreshold(pval, yval2)
epsilon, f1

<ipython-input-92-c5a1372ada03>:9: RuntimeWarning: invalid value encountered in long_scalars
  precision=tp/(tp+fp)





(1.3772288907613575e-18, 0.6153846153846154)

检查异常样本数：，符合答题要求。

out_index=np.where(p<epsilon)
len(out_index[0])

117

2 Recommender Systems

在这部分实验中，将实现协同过滤学习算法并将其应用于电影评分数据集。数据集由级评分组成，数据集有用户和电影。在本实验的下一部分中，函数cofiCostFunc：计算 co-fit 目标函数和梯度将被实现。实现代价函数和梯度后，函数fmincg将用于学习协同过滤的参数。

2.1 Movie ratings dataset

数据集ex8 movies.mat中的变量有Y和R，其中矩阵Y()是不同电影的不同用户的评分，行数为电影数目，列数为用户数目；矩阵R是二进制矩阵，表示用户对电影有评分，$R(i, j)=0jiR(i, j) = 0$的项，从而向用户推荐预测收视率最高的电影。

在本实验中，将使用矩阵X和Theta：

X第行代表第个电影的特征向量$ x^{(i)}\in R{100}$，`Theta`矩阵的第$j$列代表第$j$用户的参数向量$\theta{(j)}\in R^{100}n_m\times 100n_u\times 100$的矩阵。

data=loadmat("./data/ex8_movies.mat")
data.keys()

dict_keys(['__header__', '__version__', '__globals__', 'Y', 'R'])

Y,R=data['Y'],data['R']
nm,nu=Y.shape#y(i,j)∈[0,5],0表示未评分
Y.shape,R.shape

((1682, 943), (1682, 943))

首先平均第一部电影的收视率（有些人没有给这部电影打分）。

Y[0].sum()/R[0].sum()

3.8783185840707963

plt.figure(figsize=(8,8*(1692/943)))
plt.imshow(Y,cmap="rainbow")
plt.colorbar()#显示不同颜色对应的值
plt.xlabel("Users ({})".format(nu))
plt.ylabel("Movies ({})".format(nm))
plt.show()

​​​

​​​

2.2 Collaborative filtering learning algorithm（协同过滤学习算法）

我们现在将开始实现协同过滤学习算法。将从实现成本函数开始（没有正则化）。电影推荐中的协同过滤算法考虑一组维参数向量和，其中模型预测用户对电影的评分。给定电影的用户评分数据集，学习参数向量和以获得最小化成本函数的最佳拟合。

写函数cofiCostFunc：计算协同过滤算法的代价函数和梯度。需要传入的参数是矩阵X和Theta。为了使用现成的最小化函数如fmincg，参数X和Theta需要扩展为一维向量参数。

data=loadmat("./data/ex8_movieParams.mat")
data.keys()

dict_keys(['__header__', '__version__', '__globals__', 'X', 'Theta', 'num_users', 'num_movies', 'num_features'])

X,Theta,nu,nm,nf=data['X'],data['Theta'],data['num_users'],data['num_movies'],data['num_features']
nu,nm,nf=map(int,(nu,nm,nf))
nu,nm,nf

(943, 1682, 10)

减小数据集的大小并加快算法速度：

nu,nm,nf=4,5,3
X=X[:nm,:nf]
Theta=Theta[:nu,:nf]
Y=Y[:nm,:nu]
R=R[:nm,:nu]

X.shape,Theta.shape

((5, 3), (4, 3))

2.2.1 Collaborative filtering cost function

协同过滤算法的成本函数（无正则化）：

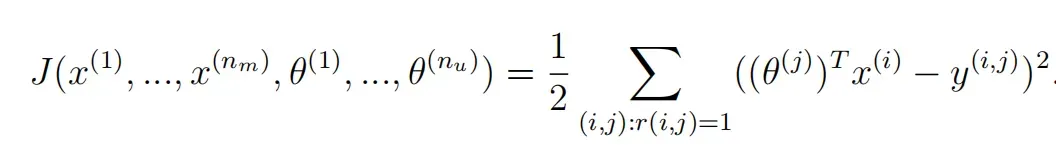
添加正则化代价函数：协同过滤算法的参数不需要有偏差，可以正则化。

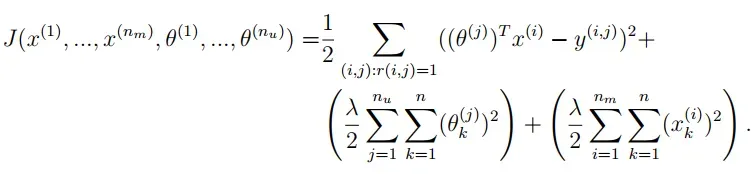
接下来编写函数cofiCostFunc：返回代价函数变量J。累加用户和电影（）的成本。运行函数期待答案：没有正则化的代价函数结果大约为；带有正则化的成本函数大约为。

def serialize(X,Theta):#将X和Theta展开成一维
    return np.r_[X.flatten(),Theta.flatten()]

def deserialize(seq,nm,nu,nf):
    return seq[:nm*nf].reshape(nm,nf),seq[nm*nf:].reshape(nu,nf)

def cofiCostFunc(seq,Y,R,nm,nu,nf,l=0):
    #Y : 评分矩阵 (nm, nu)
    #R ：0-1矩阵，用户j对电影i有无评分
    #X:(nm,nf)每行表示电影i的nf个特征
    #Theta:(nu,nf)每行表示用户i的nf个特征
    X,Theta=deserialize(seq, nm, nu, nf)
    error=0.5*np.sum(np.multiply(np.power(X@Theta.T-Y,2),R))
    reg1=0.5*l*np.sum(np.power(Theta,2))#加入正则化
    reg2=0.5*l*np.sum(np.power(X,2))
    return error+reg1+reg2

seq=serialize(X, Theta)
cofiCostFunc(seq, Y, R, nm, nu, nf),cofiCostFunc(seq, Y, R, nm, nu, nf,1.5)

(22.224603725685675, 31.34405624427422)

2.2.2 Collaborative filtering gradient

现在要实现梯度函数（没有正则化），编写一个函数cofiGradient，它返回变量X_grad（与X相同的比例）和Theta_grad（与Theta相同的比例），将两个变量展开为单个向量以返回它们的梯度。写一个函数checkCostFunction来检查梯度函数，如果函数实现正确，那么解析梯度和数值梯度是很好的匹配。

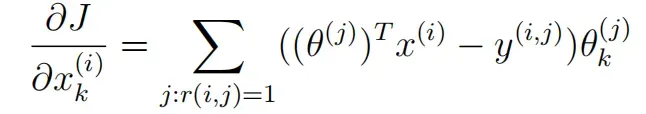
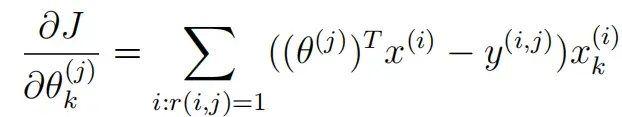
添加正则化梯度函数：

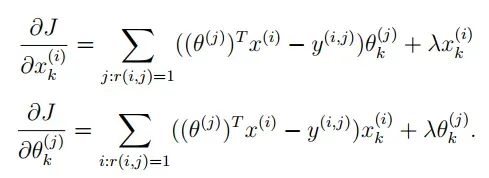
def cofiGradient(seq,Y,R,nm,nu,nf,l=0):
    X,Theta=deserialize(seq, nm, nu, nf)
    X_grad=np.multiply(((X@Theta.T)-Y),R)@Theta+l*X
    Theta_grad=np.multiply(((X@Theta.T)-Y),R).T@X+l*Theta
    return serialize(X_grad, Theta_grad)

def checkCostFunction(seq,Y,R,nm,nu,nf,l=0):
    grad=cofiGradient(seq,Y,R,nm,nu,nf,l)

    e=0.0001#Δ值
    len_seq=len(seq)
    e_vec=np.zeros(len_seq)#向量的渐变值
    for i in range(10):
        idx=np.random.randint(0,len_seq)
        e_vec[idx]=e
        loss1=cofiCostFunc(seq-e_vec,Y,R,nm,nu,nf,l)
        loss2=cofiCostFunc(seq+e_vec,Y,R,nm,nu,nf,l)
        num_grad=(loss2-loss1)/(2*e)
        e_vec[idx]=0
        diff=np.linalg.norm(num_grad-grad[idx])/np.linalg.norm(num_grad+grad[idx])
        print('num_grad:%.15f \t grad[idx]:%.15f \t 差值%.15f' %(num_grad, grad[idx], diff))

print("Checking gradient with lambda = 0:")
checkCostFunction(serialize(X,Theta), Y, R, nm, nu, nf)
print("\nChecking gradient with lambda = 1.5:")
checkCostFunction(serialize(X,Theta), Y, R, nm, nu, nf, l=1.5)

Checking gradient with lambda = 0:
num_grad:4.742718424690651 	 grad[idx]:4.742718424695921 	 差值0.000000000000556
num_grad:-10.568020204448914 	 grad[idx]:-10.568020204450614 	 差值0.000000000000080
num_grad:-0.803780061460202 	 grad[idx]:-0.803780061452057 	 差值0.000000000005067
num_grad:-0.568195965513496 	 grad[idx]:-0.568195965515757 	 差值0.000000000001990
num_grad:-7.160044429745938 	 grad[idx]:-7.160044429740946 	 差值0.000000000000349
num_grad:7.575703079698570 	 grad[idx]:7.575703079709334 	 差值0.000000000000710
num_grad:-0.383582784628800 	 grad[idx]:-0.383582784622124 	 差值0.000000000008702
num_grad:1.164413669449971 	 grad[idx]:1.164413669446225 	 差值0.000000000001609
num_grad:7.575703079698570 	 grad[idx]:7.575703079709334 	 差值0.000000000000710
num_grad:-0.766778776704058 	 grad[idx]:-0.766778776703673 	 差值0.000000000000251

Checking gradient with lambda = 1.5:
num_grad:0.129856157187191 	 grad[idx]:0.129856157163688 	 差值0.000000000090497
num_grad:0.482440977869203 	 grad[idx]:0.482440977879083 	 差值0.000000000010239
num_grad:1.092897577699148 	 grad[idx]:1.092897577688307 	 差值0.000000000004960
num_grad:1.092897577699148 	 grad[idx]:1.092897577688307 	 差值0.000000000004960
num_grad:-0.892473343601097 	 grad[idx]:-0.892473343597432 	 差值0.000000000002053
num_grad:4.901853273224788 	 grad[idx]:4.901853273231165 	 差值0.000000000000650
num_grad:-0.647874841526175 	 grad[idx]:-0.647874841514519 	 差值0.000000000008996
num_grad:1.092897577699148 	 grad[idx]:1.092897577688307 	 差值0.000000000004960
num_grad:-0.647874841526175 	 grad[idx]:-0.647874841514519 	 差值0.000000000008996
num_grad:2.101362561361952 	 grad[idx]:2.101362561388682 	 差值0.000000000006360

2.3 Learning movie recommendations（电影推荐）

完成协同过滤算法的代价函数和梯度后，就可以训练电影推荐算法了。首先获取所有电影的名称和编号，然后输入用户对电影的偏好，得到用户的电影推荐。

movies=[]#电电影列表
with open("./data/movie_ids.txt","r",encoding='gbk') as f:
    for line in f:
        movie=line.strip().split(' ')#移除字符串头尾空格
        movies.append(' '.join(movie[1:]))
movies=np.array(movies)

ratings = np.zeros((1682, 1))
#接用参考博客的数据来设置喜好值
ratings[0] = 4
ratings[6] = 3
ratings[11] = 5
ratings[53] = 4
ratings[63] = 5
ratings[65] = 3
ratings[68] = 5
ratings[97] = 2
ratings[182] = 4
ratings[225] = 5
ratings[354] = 5

ratings.shape

(1682, 1)

将用户的评分向量添加到现有数据集中，用于模型中。矩阵Y()是不同电影的不同用户的评分，行数为电影数目，列数为用户数目；矩阵R是二进制矩阵，表示用户对电影有评分，$R(i, j)=0jiR(i, j) = 0$的项，从而向用户推荐预测收视率最高的电影。

data=loadmat("./data/ex8_movies.mat")
Y=data['Y']
R=data['R']

Y.shape,R.shape

((1682, 943), (1682, 943))

Y=np.append(ratings,Y,axis=1)
R=np.append(ratings!=0,R,axis=1)

Y.shape,R.shape

((1682, 944), (1682, 944))

初始化参数矩阵X、Theta：

nm,nu=Y.shape
nf=10
l=10
X=np.random.random(size=(nm,nf))
Theta=np.random.random(size=(nu,nf))
seq=serialize(X, Theta)

X.shape,Theta.shape,seq.shape

((1682, 10), (944, 10), (26260,))

对数据进行归一化处理，这样一个完全没有评分的特征最终会得到一个非零值，因为最后会加回平均值。其中，只对有分数的数据进行平均，没有分数的数据不包括在内，都需要用R矩阵来判断。

def normalizeRatings(Y,R):
    Y_mean=((Y.sum(axis=1))/(R.sum(axis=1))).reshape(-1,1)
    Y_norm=np.multiply(Y-Y_mean,R)
    return Y_norm,Y_mean

Y_norm,Y_mean=normalizeRatings(Y,R)

Y_norm.shape,Y_mean.shape

((1682, 944), (1682, 1))

学习模型训练：

import scipy.optimize as opt
res=opt.minimize(fun=cofiCostFunc,x0=seq,args=(Y_norm,R,nm,nu,nf,l),method='TNC',jac=cofiGradient)#运行1min~2min

res

     fun: 70124.80723141175
     jac: array([ 0.12481091,  3.80257643,  4.25142191, ..., -0.2913018 ,
        0.386691  ,  0.7792457 ])
 message: 'Max. number of function evaluations reached'
    nfev: 100
     nit: 9
  status: 3
 success: False
       x: array([0.73096179, 0.16482085, 0.39889075, ..., 0.30653932, 0.17673335,
       0.97425473])

训练好的参数：X和Theta，使用这些参数向用户提供电影推荐。

X_train,Theta_train=deserialize(res.x,nm,nu,nf)

X_train.shape,Theta_train.shape

((1682, 10), (944, 10))

最后，使用训练好的参数模型推荐电影：

predition=X_train@Theta_train.T
user_predition=predition[:,0]+Y.mean()
idx=np.argsort(-user_predition)#降序排序，得到下标

idx.shape

(1682,)

user_predition[idx][:10]

array([4.03635302, 3.96571345, 3.86437942, 3.8627442 , 3.86094835,
       3.85971196, 3.83496685, 3.83174567, 3.71952258, 3.70899912])

print("Top recommendations for you:")
for i in range(10):
    print('Predicting rating %.1f for movie %s'%(user_predition[idx[i]],movies[idx[i]]))#5分制

print("\nOriginal ratings provided:")
for i in range(len(ratings)):
    if ratings[i] > 0:
        print('Rated %d for movie %s'% (ratings[i],movies[i]))

Top recommendations for you:
Predicting rating 4.0 for movie Star Wars (1977)
Predicting rating 4.0 for movie Raiders of the Lost Ark (1981)
Predicting rating 3.9 for movie Empire Strikes Back, The (1980)
Predicting rating 3.9 for movie Titanic (1997)
Predicting rating 3.9 for movie Good Will Hunting (1997)
Predicting rating 3.9 for movie Shawshank Redemption, The (1994)
Predicting rating 3.8 for movie Braveheart (1995)
Predicting rating 3.8 for movie Return of the Jedi (1983)
Predicting rating 3.7 for movie Usual Suspects, The (1995)
Predicting rating 3.7 for movie Schindler's List (1993)

Original ratings provided:
Rated 4 for movie Toy Story (1995)
Rated 3 for movie Twelve Monkeys (1995)
Rated 5 for movie Usual Suspects, The (1995)
Rated 4 for movie Outbreak (1995)
Rated 5 for movie Shawshank Redemption, The (1994)
Rated 3 for movie While You Were Sleeping (1995)
Rated 5 for movie Forrest Gump (1994)
Rated 2 for movie Silence of the Lambs, The (1991)
Rated 4 for movie Alien (1979)
Rated 5 for movie Die Hard 2 (1990)
Rated 5 for movie Sphere (1998)

用非标准化数据重新训练Y：

Y_norm = Y - Y.mean()
Y_norm.mean()

4.6862111343939375e-17

import scipy.optimize as opt
res=opt.minimize(fun=cofiCostFunc,x0=seq,args=(Y_norm,R,nm,nu,nf,l),method='TNC',jac=cofiGradient)#运行了2min38s

res

     fun: 69380.70267946126
     jac: array([ 3.22931558e-06,  4.74670755e-06,  1.53795013e-06, ...,
       -1.04391592e-06,  1.12803573e-06, -5.47338254e-07])
 message: 'Converged (|f_n-f_(n-1)| ~= 0)'
    nfev: 1430
     nit: 56
  status: 1
 success: True
       x: array([0.75326985, 0.44698399, 0.4576434 , ..., 0.36815454, 0.46085362,
       0.66916822])

X_train,Theta_train=deserialize(res.x,nm,nu,nf)
predition=X_train@Theta_train.T
user_predition=predition[:,0]+Y.mean()
idx=np.argsort(-user_predition)#降序排序，得到下标

user_predition[idx][:10]

array([4.28262534, 4.11498853, 3.98044977, 3.9058028 , 3.88817712,
       3.87460875, 3.87178834, 3.86527196, 3.76237659, 3.75394194])

print("Top recommendations for you:")
for i in range(10):
    print('Predicting rating %.1f for movie %s'%(user_predition[idx[i]],movies[idx[i]]))

print("\nOriginal ratings provided:")
for i in range(len(ratings)):
    if ratings[i] > 0:
        print('Rated %d for movie %s'% (ratings[i],movies[i]))

Top recommendations for you:
Predicting rating 4.3 for movie Titanic (1997)
Predicting rating 4.1 for movie Star Wars (1977)
Predicting rating 4.0 for movie Raiders of the Lost Ark (1981)
Predicting rating 3.9 for movie Good Will Hunting (1997)
Predicting rating 3.9 for movie Shawshank Redemption, The (1994)
Predicting rating 3.9 for movie Braveheart (1995)
Predicting rating 3.9 for movie Return of the Jedi (1983)
Predicting rating 3.9 for movie Empire Strikes Back, The (1980)
Predicting rating 3.8 for movie Terminator 2: Judgment Day (1991)
Predicting rating 3.8 for movie As Good As It Gets (1997)

Original ratings provided:
Rated 4 for movie Toy Story (1995)
Rated 3 for movie Twelve Monkeys (1995)
Rated 5 for movie Usual Suspects, The (1995)
Rated 4 for movie Outbreak (1995)
Rated 5 for movie Shawshank Redemption, The (1994)
Rated 3 for movie While You Were Sleeping (1995)
Rated 5 for movie Forrest Gump (1994)
Rated 2 for movie Silence of the Lambs, The (1991)
Rated 4 for movie Alien (1979)
Rated 5 for movie Die Hard 2 (1990)
Rated 5 for movie Sphere (1998)