目录
1、语言L={ambn ,m>=1,n>=1},试写出文法。
2、语言L={anbncm ,m>=1,n>=1},试写出文法。
4、语言L={anbmcmdn ,m>=1,n>=1},试写出文法。
一、句型的分析
1、规范推导和规范归约
最左(右)推导:在任一步推导v=>w中,都是对符号串v的最左(右)非终结符号进行替换,称最左(右)推导。
规范推导:即最右推导。
规范句型:由规范推导所得的句型。
规范归约:规范推导的逆过程,称规范归约或最左归约。
例:
G[<标识符>]
<标识符>→<字母>|<标识符><字母>
|<标识符><数字>
<字母>→a|b|…|z|A|…|Z
<数字>→0|1|2|…|9规范推导
<标识符>
=><标识符> <字母>
=><标识符>y
=><标识符> <数字>y
=><标识符>4y
=><字母>4y
=>a4y规范归约
a4y
<≠<字母>4y
<≠ <标识符>4y
<≠ <标识符><数字>y
<≠<标识符>y
<≠ <标识符><字母>
<≠ <标识符>
2、短语、简单短语和句柄
短语:文法G[Z], ω=xuy是一句型,x,y∈V*,如有 Z=*>xUy,且U=+>u, U∈Vn, u ∈V+,称u是一个相对于非终结符号U句型ω的短语。
简单短语:文法G[Z], ω=xuy是一句型,如有 Z=*>xUy,且U=>u, U∈Vn, u ∈V+,称u是一个相对于非终结符号U句型ω的简单短语。
句柄:句型最左边的简单短语为该句型的句柄,一个句型只有一个句柄。
说明:
- 短语和简单短语必须是针对某一句型来说的,并且是该句型的一个字串。
- 短语和简单短语必须是相对某一非终结符号的。
- 两个条件缺一不可。
- 一个句型可以有几个短语和简单短语。
- 一个当前句型只有一个句柄(无二义性的文法)
- 最左归约归约的当前句型的句柄。
例:
G[S]:
S→AB
A→Aa|bB
B→a|Sb问题:给出句型baSb的短语、简单短语和句柄。
(1) S=>AB=>bBB =>baB=>baSb 且B=>Sb
(2) S=>AB =>ASb =>bBSb=>baSb 且B=>a
(3) S=>AB =+>baSb 且A=+>baSb是相对于B、句型baSb的短语且为简单短语,
a是相对于B、句型baSb的短语且为简单短语,
ba是相对A、句型baSb的短语 句柄为a。
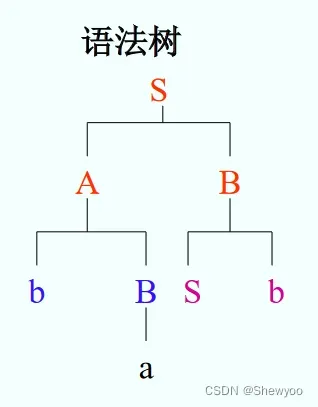
3、语法树
语法树:一个句型或句子推导过程的图示法表示,形成一棵语法树。
根:开始符号。
子树:某一非终结符号 (子树的根)及其下面的分支。
叶:树的末端结点。
语法树的全部末端结点(自左向右)形成当前句型。
例:
G[S]:
S→AB
A→Aa|bB
B→a|Sb最左推导
S=>AB
=>bBB
=>baB
=>baSb
说明:
设文法G=(Vn,Vt,P,S),对G的任何句型都能构造与之关联的、满足下列条件的一课语法树。
- 每个结点都有一个标记,此标记是V=Vn∪Vt∪ε中的一个符号。
- 树根的标记是文法的开始符号S。
- 若某一结点至少有一个分支结点,则该结点上的标记一定是非终结符号。
- 若A的结点有k个分支结点,其分支结点的标记分别为A1,A2,…,Ak,则A→A1A2…Ak一定是G的一条规则。
4、通过树来寻找短语、简单短语、句柄
短语:子树的末端结点形成的符号串。
简单子树:只有一层分支的子树。
简单短语:简单子树的末端结点形成的符号串。
例:
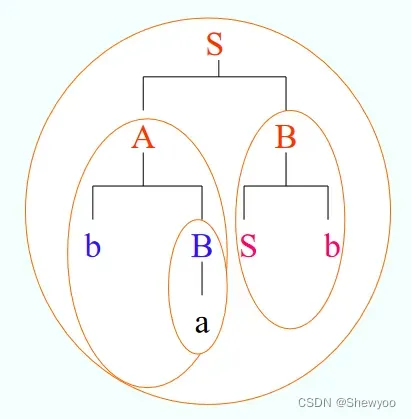
句型baSb的语法树
共有三颗子树,
三个短语:ba ,a, Sb,baSb
简单短语: a, Sb
句柄: a1、如何找短语?
从树根S开始,找S的末端结点是:baSb(也就是句型本身)
然后往下找A的末端结点是:ba
B的末端结点是:Sb
再往下只有B有末端结点是:a
2、如何找简单短语?
先找到简单子树即只有一层分支的子树;
然后简单子树的末端结点形成的符号串即简单短语。
3、如何找句柄?
找左边的简单短语
结论:
- 对于某个句型,每个推导,都有一个相应的语法树;但不同的推导也可能有相同的语法树。
- 树的末端结点形成所要推导的句型。
- 但某个句型也可能对应两棵不同的语法树,这就是文法的二义性问题
二、文法的二义性
1、文法二义性的定义
- 如果文法G的某一个句子存在两棵或两棵以上不同的语法树,则称句子是二义性的。
- 如果一文法含有二义性的句子,则称该文法是二义性的,否则该文法是无二义性的。
说明:
- 文法的二义性:某一句子有两个不同的最左(右)推导,或两个不同的最左(规范)归约。
- 文法的二义性是不可判定的:不存在一种算法。
- 证明文法的二义性只能试图找到某句子,该句子存在两颗不同的语法树或两个不同的最左(右)推导。
- 特例:若一文法G既含左递归又含右递归,则G必是二义性文法.(是经验)
例:
证明文法G[S]:S→aSb|Sb|b为二义性文法。
证明:对于句子abbb存在两个不同的最左推导
最左推导1: S=>aSb=>aSbb=>abbb
最左推导2: S=>Sb=>aSbb=>abbb
因此,句子abbb是二义性的,由于文法存在二义性的句子,所以文法G[S]是二义性的。
2、文法二义性的消除
(1)定义规定或规则
例:
G1[E]:E→E+E|E*E|(E)|i
规定:四则运算法则,成无二义性文法。
G[S]: S →if B then S else S|if B then S
规定:else跟与它最近尚未匹配的then匹配,成无二义性文法
(2)改写文法
例:
G1[E]:E→E+E|E*E|(E)|i
二义性文法,无优先关系信息,不能直接使用。
G2[E]:
E→E+T|T
T→T*F|F
F→(E)|i无二义性文法,含四则运算信息,语法分析时使用。
三、例题
1、语言L={ambn ,m>=1,n>=1},试写出文法。
G[S]:
S→AB
A→Aa|a
B→bB|b
或G[S]:
S→AB
A→aA|a
B→bB|b
2、语言L={anbncm ,m>=1,n>=1},试写出文法。
G[S]:
S→AB
A→aAb|ab
B→cB|c
3、语言L={anbbn ,n>=1},试写出文法。
G[S]:
S→aAb
A→aAb|b或G[S]:
S→aSb|A
A→abb
4、语言L={anbmcmdn ,m>=1,n>=1},试写出文法。
G[S]:
S→aSd|aAd
A→bAc|bc
5、语言L={ambn ,n>=m>=1},试写出文法。
解: 改写为等价语言 L={ambmbk ,m>=1,k>=0}
G1[S]:S→AB
A→aAb|ab
B→bB|εG2[S]:
S→aAb
A→aAb|Ab|ε
或改写为等价语言 L={ambkbm ,m>=1,k>=0}
G3[S]:
S→aSb|aAb
A→bA|ε
文章出处登录后可见!