1. 线性回归
回归概念:回归是一类可以对一个或多个自变量与因变量之间的关系进行建模的方法。机器学习领域的大多数任务通常与预测有关。预测房价,预测住院时间。
线性回归:基于几个简单的假设,自变量x和因变量y之间的关系是线性的,也就是y可以表示为x中元素的加权和,这里通常允许观测值的一些噪声。
1.1 线性模型
线性假设意味着目标可以表示为特征的加权和。

Warea和Wage称为权重,权重决定每一个特征对我们预测值的影响。b称为偏置(bias)、偏移量(offset)或者截距(intercept)。偏置是指当所有的特征都取值为0时,预测值应该是多少。
上图中的公式实际上是一个仿射变换:特征通过加权和线性变换,并通过偏置项进行平移。
在机器学习领域,我们的输入数据通常是高维数据集,
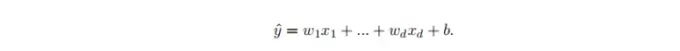
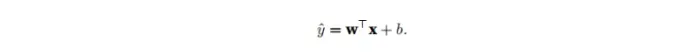
这里的x是单个数据样本的特征。用X表示整个数据集的所有样本,X的每一行都是一个样本,每一列是一种特征。
对于特征集合X,预测值y可以通过:y = Xw + b表示
![]()
这样y其实是一个n维列向量,每一行都是一个样本下计算出的结果。
给定训练数据特征X和对应的已知标签y,线性回归的目标是找到一组权重向量w和偏置b:当给定从X的同分布中取样的新样本特征时,这组权重向量和偏置能够使得新样本预测标签的误差尽可能小
无论使用什么手段来观察特征X和标签y,都可能出现少量的观测误差。我们只是假设特征与标签的潜在关系是线性的,我们会加入噪声项来考虑观测误差带来的影响。
1.2 损失函数
损失函数可以量化目标实际值与预测值之间的差距。损失值越小,拟合越好。回归问题中最常用的损失函数是平方误差函数。类似于方差
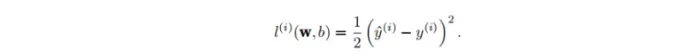
这里算的只是一个样本,为了度量模型在整个数据集上的质量,我们需要计算在训练集n个样本上的损失均值
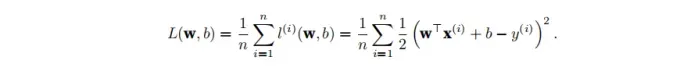
在训练模型的时候,我们想要最小化总损失,所以我们需要找到一组合适的参数来最小化总损失: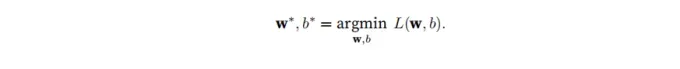
1.3解析解
线性回归的解可以用一个公式简单地表达出来,这类解叫做解析解。首先,我们将偏置b合并到参数w中,合并的方法是在包含所有参数的矩阵中附加一列。我们的预测问题是最小化||y-Xw||^2。下面找极小值点。对w求导。

最终解析解: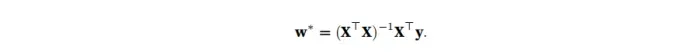
但并非所有问题都有分析解决方案。
1.4 随机梯度下降
进行梯度下降的最简单方法是计算损失函数相对于模型参数(实际上是梯度)的导数。随机抽取一小批样本并进行梯度下降。
首先对一个 mini-batch 进行采样,计算 mini-batch 的平均损失对模型参数的导数,最后将梯度乘以一个预定整数并从当前参数值中减去它。
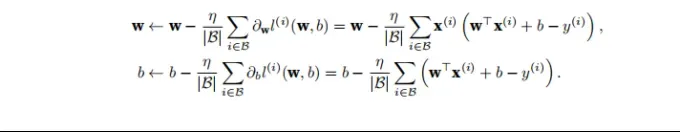
|B|表⽰每个⼩批量中的样本数,这也称为批量⼤⼩(batch size)。η表⽰学习率(learning rate)。批量⼤⼩和学习率的值通常是⼿动预先指定,⽽不是通过模型训练得到的。
这些在训练期间可以调整但不能更新的参数成为超参数。调优是选择超参数的过程。超参数通常由我们根据训练迭代的结果进行调整,这些结果在独立的验证数据集上进行评估。
在训练预定次数的迭代后,记录模型的参数估计值。这些参数估计只能让损失值慢慢收敛,而不能在有限的迭代次数内达到最小值。
难度:找到一组参数以在从未见过的数据上实现低损失,泛化问题。
1.5 用模型进行预测
使用给定模型估计新训练数据的输出。
1.6 矢量化加速
在训练模型时,我们希望同时处理多个样本。向量化计算。
- for循环加法:
import math
import time
import numpy as np
import torch
from d2l import torch as d2l
n = 10000
a = torch.ones(n)
b = torch.ones(n)
class Timer:
"""记录多次运行时间"""
def __init__(self):
self.times = []
self.start()
def start(self):
"""启动计时器"""
self.tik = time.time() # 采集当前时间
# 计算程序的运行时间 当前时间减去开始时间
def stop(self):
"""停止计时器并且将时间记录在列表中"""
self.times.append(time.time() - self.tik)
return self.times[-1] # 返回最新的时间差
def sum(self):
"""返回时间总和"""
return sum(self.times)
def cumsum(self):
"""返回累计时间"""
return np.array(self.times).cumsum().tolist()
c = torch.zeros(n)
timer = Timer()
for i in range(n):
c[i] = a[i] + b[i]
print(f'{timer.stop():.5f} sec')
结果:0.12576 sec
- 矢量化
timer.start()
d = a + b
print(f'{timer.stop():.5f} sec')
结果:0.00096 sec
1.7 正态分布与平方损失
正态分布也称为高斯分布,正态分布的概率密度函数为: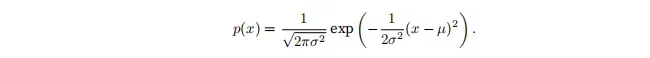
def normal(x,mu,sigma):
p = 1 / math.sqrt(2 * math.pi * sigma **2)
return p * np.exp(-0.5 / sigma**2 * (x - mu)**2)
x = np.arange(-7,7,0.01)
params = [(0,1),(0,2),(3,1)]
d2l.plot(x, [normal(x, mu, sigma) for mu, sigma in params], xlabel='x',
ylabel='p(x)', figsize=(4.5, 2.5),
legend=[f'mean {mu}, std {sigma}' for mu, sigma in params])
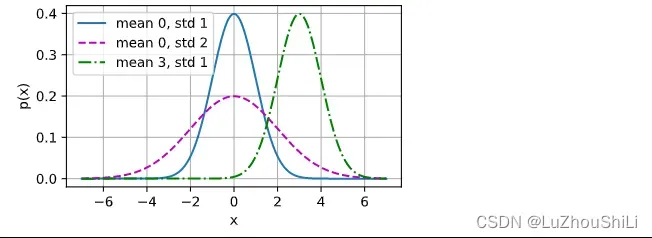
我们假设观测值包含噪声,并且噪声服从正态分布
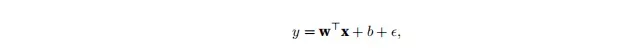
写出w,b的极大似然估计函数:![]()
1.8 从线性回归到深度网络
线性回归实际上是一个单层神经网络: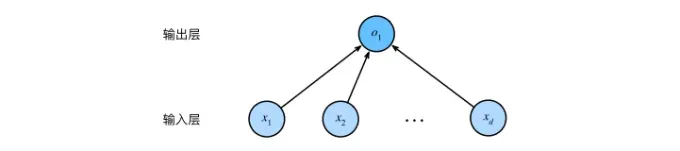
上图中,输入是x1,x2,xd,因此输入层中的输入数是d。网格的输出为o1,输出层的输出数是1。图中的神经网络的层数是1,我们将线性回归模型是为仅有单个人工神经元组成的神经网络,或者称为单层神经网络。
对于线性回归,每个输入都连接到输出,这种变换称为全连接层。
文章出处登录后可见!
