内容

一、简介

二、逐步讲解r语言程序

1.导入数据集并查看数据集的基本情况

2.查看数据分布情况

3.查看自变量因变量的散点图，判断线性关系

4.添加线性模型

5.回归，并查看回归的基本数据项

6.假设检验 F检验 ANOVA

7.预测与残差

8.残差

9.结论

10.模型的修正

一、简介

上次讲了基础理论，今天讲一个例子：

我们使用的数据集是每周啤酒销售数据集：

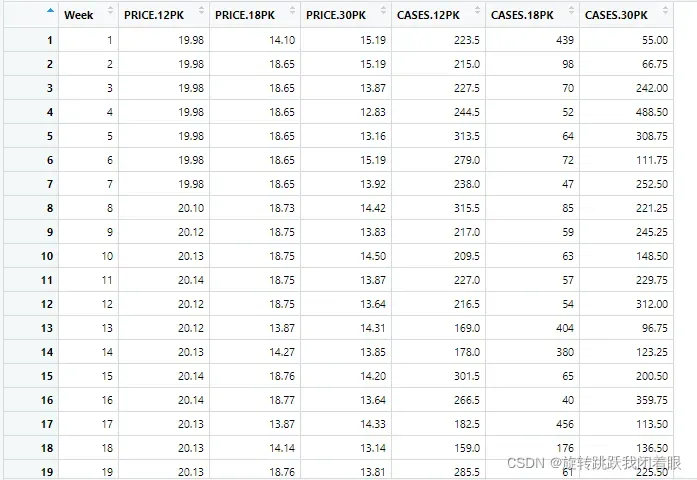
二、逐步讲解r语言程序

1.导入数据集并查看数据集的基本情况

x=read.csv(file.choose(), header=TRUE)
names(x)
summary(x)

结果：

2.查看数据分布情况

plot(x$Week,x$PRICE.18PK,xlab="Week",ylab="Price.18PK")
lines(x$PRICE.18PK)

结果：

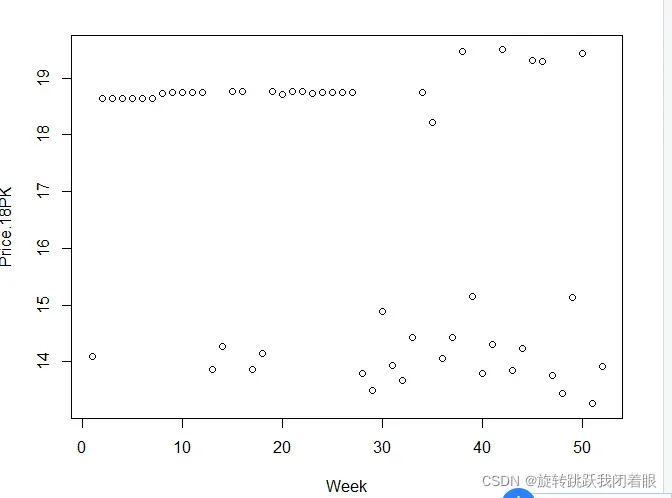
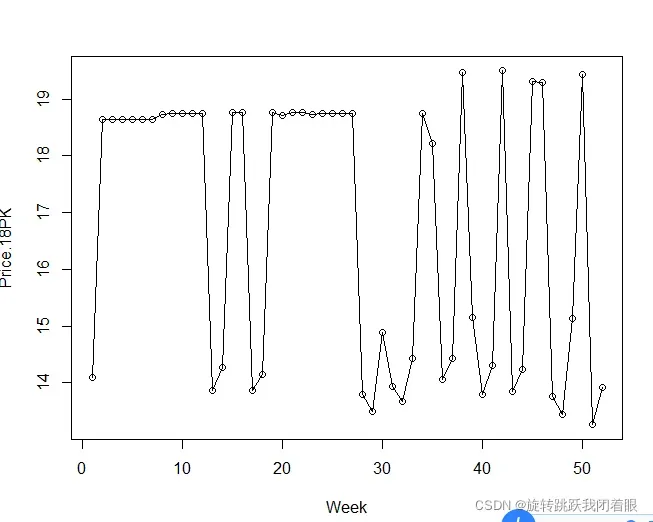
3.查看自变量因变量的散点图，判断线性关系

plot(x$PRICE.18PK,x$CASES.18PK, xlab="Price 18 Pack"
, ylab="Case 18 Pack", main="Scatter Plot")

结果：

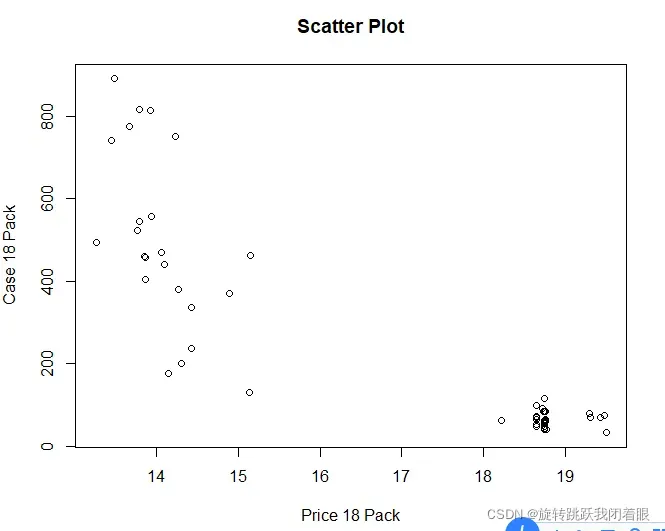
4.添加线性模型

fitModel<-lm(CASES.18PK~PRICE.18PK, data=x)
abline(fitModel, col="red")

结果：

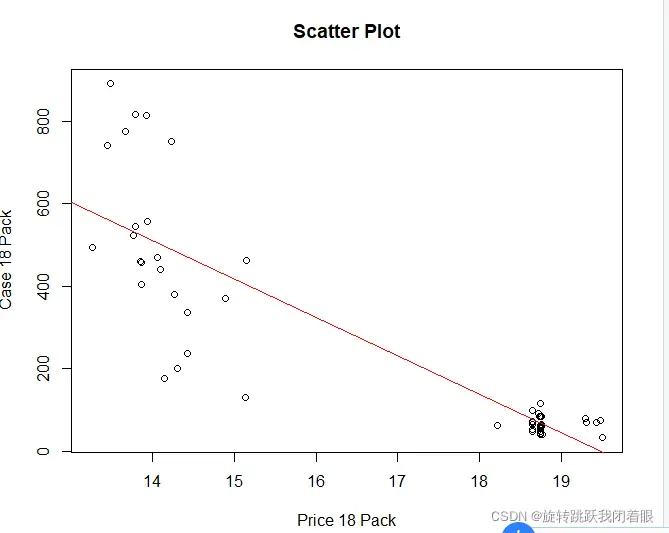
5.回归，并查看回归的基本数据项

regResult<-summary(fitModel)
regResult

结果：

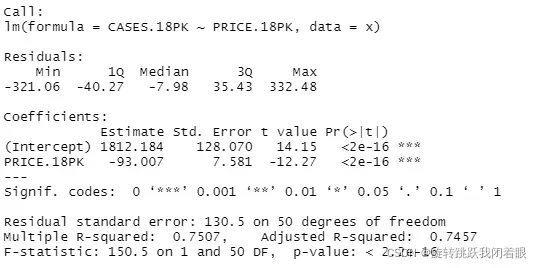
我们可以看到各种数据，用来判断模型是否合理。

6.假设检验 F检验 ANOVA

summary.aov(fitModel)

结果：

相关性非常显着。

7.预测与残差

residualData<-resid(fitModel)
predicted<-predict(fitModel)
plot(predicted,residualData, xlab="Predicted Values", ylab="Residuals", col="red")

结果：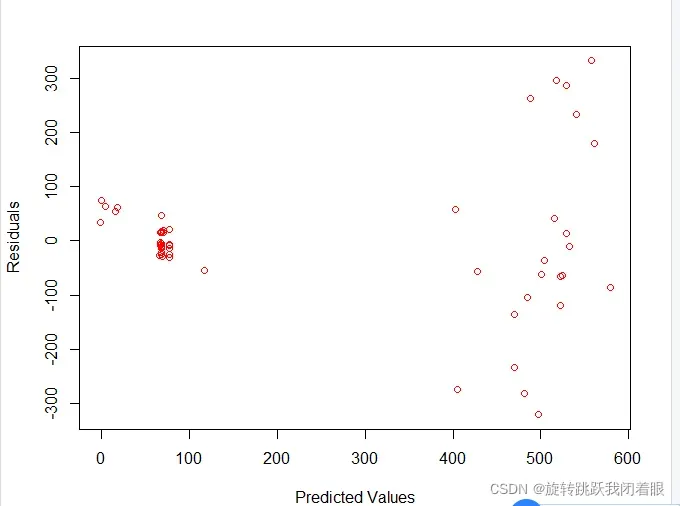

我们发现这个拟合模型是有问题的

这是一个问题：当做出更大的预测时，模型会产生更大的错误

回归模型中的一个假设是，无论自变量的值如何，误差在所有点上都应该具有相同的方差。

因此，残差应该呈正态分布，均值为 0

但是，该模型在较大的预测值下显然过于离散。这是异方差的证据！ ！

所有预测级别的具有不同方差的错误！这叫做异方差问题！

8.残差

plot(x$Week,residualData)
abline(0, 0, col="red")

结果：

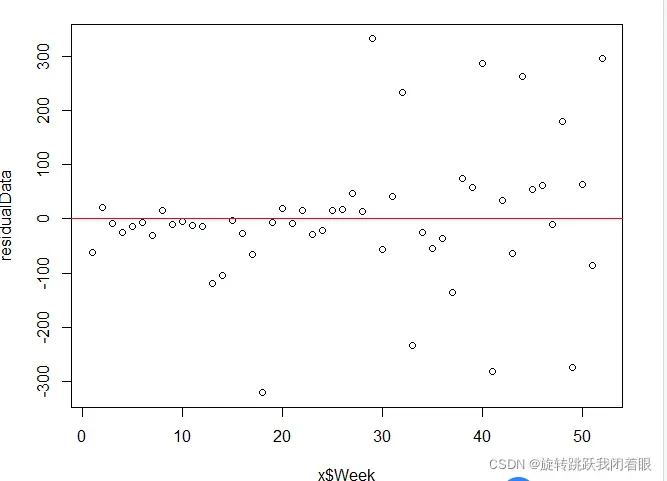
我们发现了另一个问题。显然，在时间序列上，上半年的残差明显低于下半年。那么，可以说是啤酒厂在下半年出现了销量暴增，或者说是公司存在明显的人为控制。销售的事情，这不是自然的。大多数价格操纵和销售高峰发生在下半年！

我们希望残差是平坦的，而不是发散的

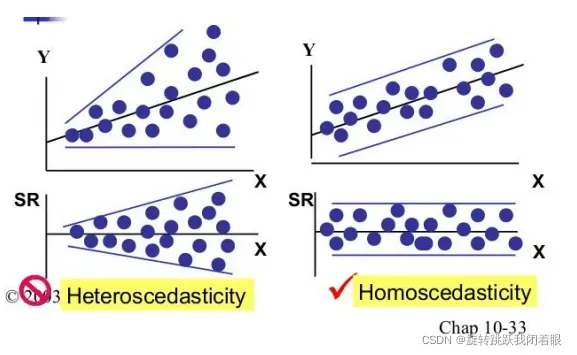
9.结论

在如此大的价格范围内，啤酒销量与啤酒价格之间的关系显然不是线性的。该模型违反了误差的同方差性和正态分布假设。

并不是所有具有高R2值的模型都是好的！

10.模型的修正

以前的模型(每箱价格和每箱18包出售)的结果很糟糕，因为它对数据中的模式的性质做出了错误的假设。

一种经常使用且经常成功的策略是寻找原始变量的转换，使曲线变直，误差归一化，和/或利用时间维度。

其他策略包括：

• 添加新变量
  
• 将数据设置为子集
  

标准方法是在拟合回归模型之前对自变量和因变量应用自然对数变换。

当一个简单的线性回归模型被拟合到记录变量上时，斜率系数表示因变量的预测百分比变化/自变量的百分比变化，而不管它们当前的水平。

因此，预计自变量的大变化将导致边际效应的复合，而不是它们的线性外推。

install.packages("dplyr")
library("dplyr")
x<-mutate(x,ln_CASES.18PK=log10(x$CASES.18PK),ln_PRICE.18PK=log10(x$PRICE.18PK))
fitModel1<-lm(ln_CASES.18PK~ln_PRICE.18PK, data=x)
summary(fitModel1)

residualData<-resid(fitModel1)
predicted<-predict(fitModel1)
plot(predicted,residualData, xlab="Predicted Values", ylab="Residuals", col="red")

x<-mutate(x,ln_PRICE.12PK=log10(x$PRICE.12PK), ln_PRICE.30PK=log10(x$PRICE.30PK))
fitModel2<-lm(ln_CASES.18PK~ln_PRICE.18PK+ln_PRICE.12PK+ln_PRICE.30PK,data=x)
summary(fitModel2)

结果：

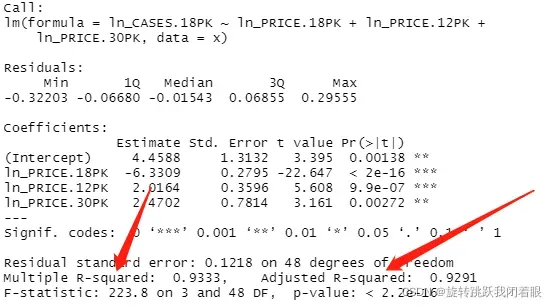
R2更好了！

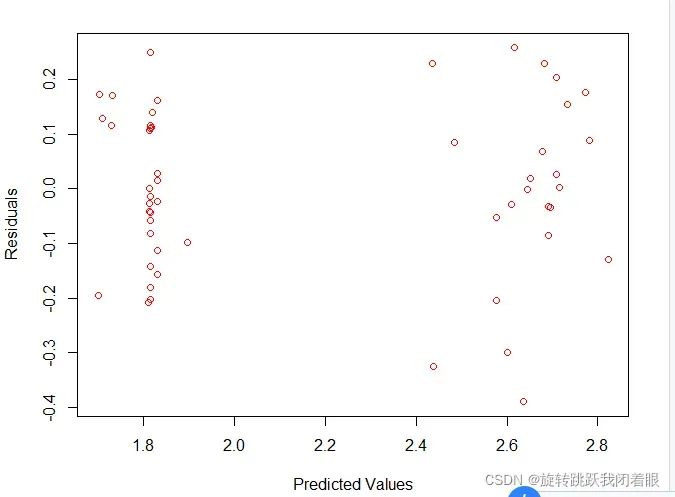
误差的方差更均匀地分布在所有预测值中。

当然，我们也可以添加其他变量来使模型更好。这里不多说。