前言
从这一期开始,我们准备介绍一系列经典机器学习算法模型,主要包括逻辑回归,支持向量机,决策树,因子分析,主成分分析,K-Means聚类,多元线性回归,时间序列,关联规则,朴素贝叶斯,隐式马尔可夫,协同过滤,随机森林,XGBoost,LightGBM等,一般会涵盖算法模型的引入背景,算法模型依赖的数学原理,算法模型的应用范围,算法模型的优缺点及改进建议,工程实践案例等。既适合刚入门机器学习的新手,也适合有一定基础想要进一步掌握算法模型核心要义的读者,其中不免会涵盖许多数学符号,公式以及推导过程,如果你觉得晦涩难懂,可以来”三行科创”微信交流群和大家一起讨论交流。
从对数转换到逻辑回归
逻辑回归是最常见的一种用于二分类的算法模型,由于其数学原理简单易懂,作用高效,实际应用非常广泛,虽然带回归二字,实则是分类模型,下面从logit变换开始。
当我们研究某个结果与一系列因素
之间的关系时,最直接的思路就是建立因变量与自变量之间的多元线性关系模型
其中为模型的参数,如果因变量是数值型的话,可以解释成某某因素
变化了多少导致结果
发生了多少变化,如果因变量
是用来刻画结果是否(0-1)发生?或者更一般的来刻画特定结果发生的概率(0~1)呢?这时候因素
变化导致结果
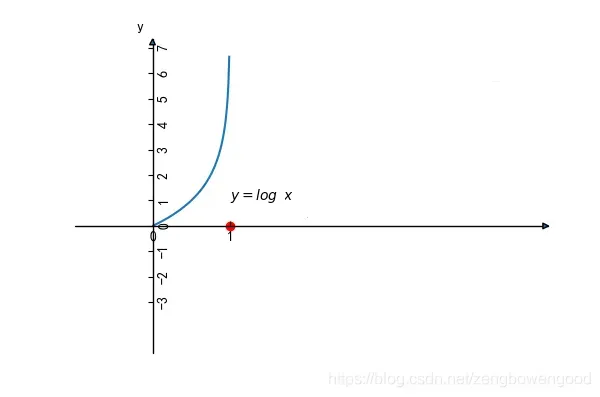
的变化恐怕微乎其微,有时候甚至忽略不计。然而现实生活中,我们知道某些关键因素会直接导致某一结果的发生,如亚马逊雨林一只蝴蝶偶尔振动翅膀,就会引起两周后美国德克萨斯州的一场龙卷风。于是,我们需要让不显著的线性关系变得显著,使得模型能够很好解释随着因素的变化,结果也会发生显著的变化,这时候,人们想到了对数(logit)变换,下图是对数函数图像
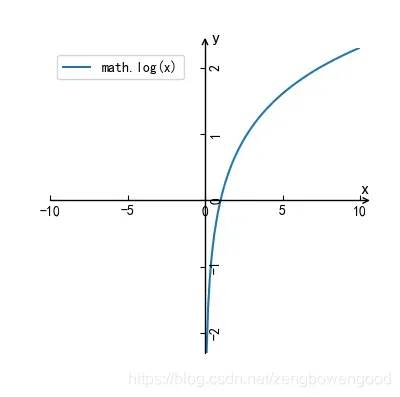
从对数函数的图像来看,之间因变量的变化是非常迅速的,也就是说,自变量的微小变化会导致因变量的巨大变化,这与之前的想要的效果。因此,对因变量进行对数变换,右侧依然保持线性关系,有下式
虽然上式解决了因变量随着自变量变化的敏感性问题,同时也约束了的取值范围在
。我们知道概率是用来描述某件事发生的可能性,一件事情发生与否,更应该是调和对称的,也就是说该事件发生与不发生有对立性,结果可以走向必然发生(发生概率为1),也可以走向必然不发生(发生概率为0),概率的取值范围为
,而等式左边
的取值范围是
,所以需要进一步压缩,又引进了几率。
几率(odd)是指事件发生的概率与不发生的概率之比,假设事件 A 发生的概率为,不发生的概率为
,那么事件 A 的几率为
概率正好反映了一个事件的两个对立面,具有很好的对称性。我们来看看概率和概率之间的关系。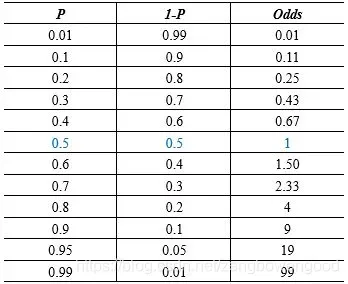
首先,我们看到概率从0.01不断增大到 0.99,几率也从0.01随之不断变大到99,两者具有很好的正相关系,我们再对向两端取极限有
因此,概率的取值范围为,符合我们之前对因变量取值范围的假设。
正因为概率和概率有如此密切的互惠关系,所以想知道是否可以用概率代替概率来描述结果发生的概率,这样既能满足结果对影响因素,还要满足发生与否的对称性。 , 那么下面的公式
现在,我们稍微改一下,让等式左边的对数变成自然对数,把等式右边变成向量积形式,我们有
其中、
,我们解决
其中是自然常数,保留5位小数是2.71828。这就是我们常见的逻辑模型表达式,作出其函数图像如下
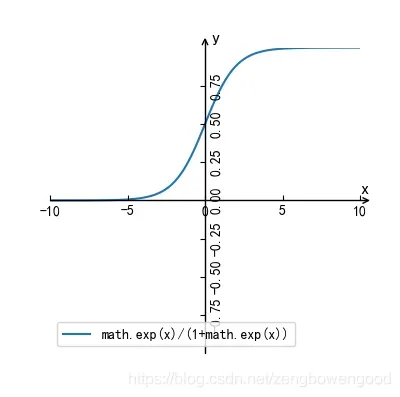
我们看到逻辑模型的函数图像是一条S型曲线,又名sigmoid曲线,以为对称中心,随着自变量
不断增大,其函数值不断增大接近1,随自变量
不断减小,其函数值不断降低接近0,函数的取值范围在
之间,且函数曲线在中心位置变化速度最快,在两端的变化速率最慢。
从上面的操作,我们可以看到逻辑回归模型从最初的线性回归模型基础上对因变量进行 对数变换,使得因变量对自变量显著,同时约束因变量取值范围为0到正无穷大,然后用几率表示概率,最后求出概率关于自变量的表达式,把线性回归的结果压缩在范围内,这样最后计算出的结果是一个0到1之间的概率值,表示某事件发生的可能性大小,可以做概率建模,这也是为什么逻辑回归叫逻辑回归,而不叫逻辑分类了。
二项式逻辑回归模型
既然逻辑回归把输出结果压缩到连续的区间,而不是离散的 0 或者1,然后我们可以取定一个阈值,通常以0.5为阈值,通过对比输出结果与阈值的大小关系而定,如果计算出来的概率大于等于0.5,则将结果归为一类 (1),如果计算出来的概率小于0.5,则将结果归为另一类 (0),用分段函数写出来便是
这样逻辑回归就可以用来进行2分类了,在本文中,不特别指出,均指二项逻辑回归,假设数据结构如下
| 样本 | x 1 x_1 x1 | x 2 x_2 x2 | … | x n x_n xn | y y y |
|---|---|---|---|---|---|
| 1 | x 11 x_{11} x11 | x 12 x_{12} x12 | … | x 1 n x_{1n} x1n | y 1 y_1 y1 |
| 2 | x 21 x_{21} x21 | x 22 x_{22} x22 | … | x 2 n x_{2n} x2n | y 2 y_2 y2 |
| ⋮ \vdots ⋮ | ⋮ \vdots ⋮ | ⋮ \vdots ⋮ | … | ⋮ \vdots ⋮ | ⋮ \vdots ⋮ |
| m | x m 1 x_{m1} xm1 | x m 2 x_{m2} xm2 | … | x m n x_{mn} xmn | y m y_m ym |
其中表示样本个数,
表示影响因数的个数,
取 0 或者 1。现在我们结合数据,利用条件概率分布模型给出基于概率的二项逻辑回归模型如下
其中,表示因变量所属的类别,
表示自变量,
为模型待求的参数,模型解释为在特定的因素(
)下,模型结果取1的概率和取0的概率。模型有了,接下来就需要进行机器训练,而怎么来给训练一种恰当反馈呢?答案就是损失函数,通过损失函数来评估模型学习的好坏和改进机制。
由前面阈值的取定原则,我们知道相当于我们用一个类别值代替概率值,而类别值是sigmoid 函数的两个最值,概率不可能时时刻刻都取到最值,这势必会造成误差,我们把这种误差称为损失,为了给出损失函数表达式,我们假设模型第个样本所求的概率值为
,而真实类别值可能是 0 或者 1。
当类别真实值是 1 的情况下,所求的概率值越小,越接近0,被划为类别 0 的可能性越大,被划为类别 1 的可能性越小,导致的损失越大。反之,所求的概率值
越大,越接近1,被划为类别 1 的可能性越大,被划为类别 0 的可能性越小,导致的损失越小。我们用下面的函数来描述这种变化关系
其中,,其形象大致如下
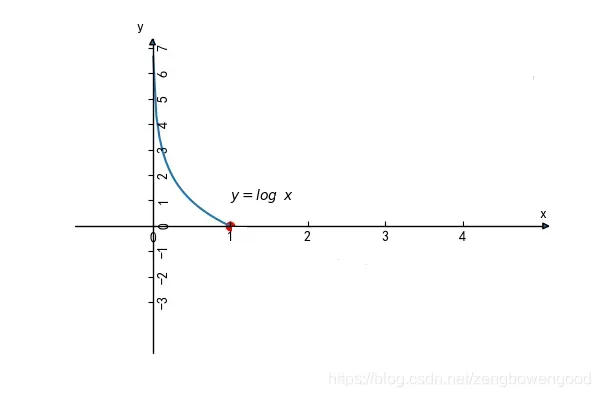
当类别真实值是0的情况下,所求的概率值越大,越接近1,其结果的类别判定更偏向于1,导致的损失越大。反之,所求的概率值
越小,越接近0,其结果的类别判断更偏向于 0,导致的损失越小。我们用下面的函数来描述这种变化关系
现在就要把两种情况结合起来,就不需要分真实值是 1 还是 0 两种情况讨论,求出其期望值,做成一个交叉熵(cross entropy)的整体损失函数如下
其中表示第
个样本的真实值(取0或者1),
是根据模型计算出来的概率值,当
时,
,当
时,
,这符合前面两种情况。
假设现在有个样本,整体损失函数为
替代
上式是二项式逻辑回归的损失函数。它是参数和
的二元函数,也称为对数似然函数。现在问题转化为以对数似然函数为目标函数的优化问题,其中
是要在模型中找到的参数。为求参数
,可求目标函数对
的偏导数,记下
求对
的偏导,主要是求解对数函数对
的偏导
其中,和
为对数底,令
,求
的值,然后带入模型学习逻辑模型参数
的值,假设
为上式得到的值,则原始二项式逻辑回归模型 方程为
逻辑回归模型的应用
由于逻辑回归模型主要用于二分类,因此逻辑回归可以用于所有涉及二分类的场景。同时,我们也可以使用逻辑回归模型来预测某事发生的概率。我们常见的逻辑回归模型应用场景有
(1) 在P2P,汽车金融等领域,根据申请人的提供的资料,预测其违约的可能性大小,进而决定是否给其贷款。
(2) 电商平台根据用于购买记录预测用户下一次是否会购买某件商品。
(3) 天涯,bbs,微博,豆瓣短评等舆论平台做情感分类器。如根据某网友对某些特定主题的历史评论数据,预测其下次对某类型的主题是否会给出正面的评论。
(4) 在医疗领域,根据病人症状,预测其肿瘤是良性的还是恶性的。
(5) 根据CT,流行病学,旅行史,检测试剂结果等特点预测某位疑似病人是否真感染新型冠状病毒。
(6) 在交通物流领域,预测某趟运输是否会拉货。
逻辑回归模型的评估
从逻辑回归模型的数学原理和确定阈值时的一刀切的方法,我们可以根据逻辑回归的这些特点来评估模型的优缺点
优势:
- 原理简单,模型清晰,运行高效。其背后的概率推导过程经得起推敲。在研究中,通常以逻辑回归模型为基准,然后尝试使用更复杂的算法,可用于大数据场景;
- 使用online learning的方式更新轻松更新参数,不需要重新训练整个模型;
- 基于概率建模,输出值落在0到1之间,并且有概率意义;
- 得到的参数
代表了各个因素对输出结果的影响,具有很强的可解释性;
- 解决过拟合的方法很多,如L1、L2正则化,L2正则化就可以解决多重共线性问题;
缺点:
- 对数据的强依赖,很多情况下需要特征工程,主要用于解决线性可分问题;
- 因为本质上是一个线性分类器,无法处理特征之间的相关性,对模型中自变量的多重共线性比较敏感。例如,将两个高度相关的自变量同时放入模型中,可能导致较弱的自变量回归的符号不符合预期,符号颠倒,正号变为负号;
- 对数变换过程是非线性的,两端变化率很小,中间变化很大,非常敏感。多区间变量变化对目标概率的影响难以区分,阈值难以确定;
- 特征空间大时,性能不好;
- 容易欠拟合,精度不高;
实际案例
学完逻辑回归算法模型的理论,就到了吃硬菜和实战案例的时候了。我们将使用 Andrew Ng 的机器学习系列中的一个案例进行扩展。
本次实践目的是利用下列数据训练出逻辑回归算法模型并给出模型的评估,从ex2data1的数据来看,这份数据是没有表头的,一共100个样本,前2列是特征值表示某位申请者两门课程的评分,第三列是标签列表示该申请者是否被接收,其中1表示被接收,0表示不被接收。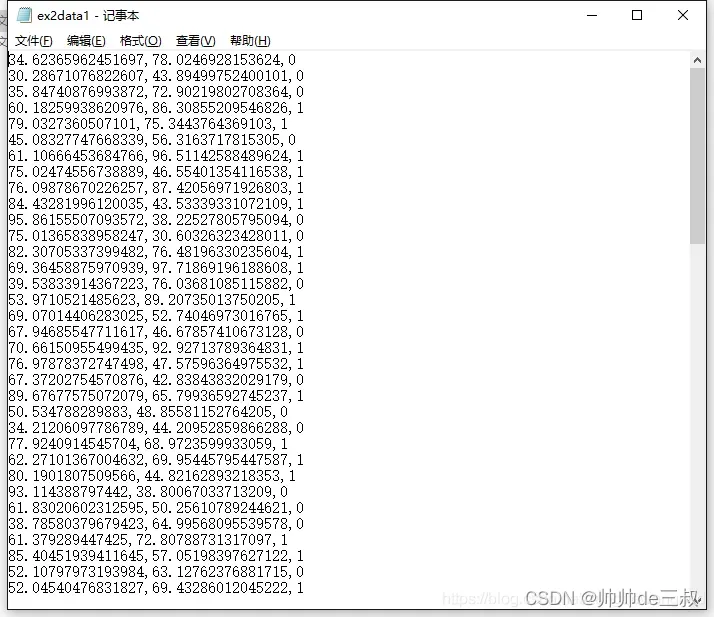
针对低维(小于等于3)数据我们可以进行可视化处理,这样可以让原数据的有些分布特征看起来更直观
def visualization(): #数据可视化
plt.figure(figsize = (6,4)) #新建画布
plt.scatter(pos[:,1], pos[:, 2], marker='+', label='admitted') #正性散点
plt.scatter(neg[:,1], neg[:,2], marker='x', label = 'unadmitted') #负性散点
plt.xlabel("exam1_score")
plt.ylabel("exam2_score")
plt.pause(2)
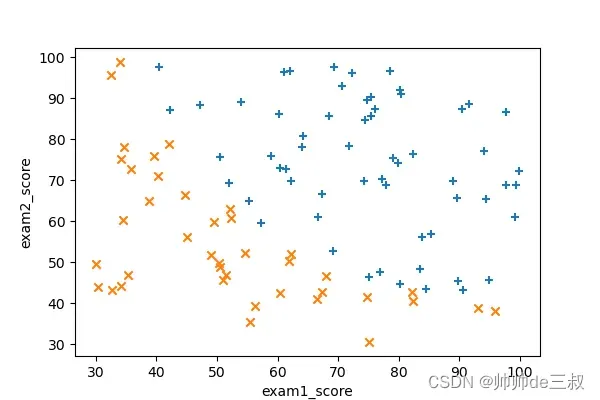
通过数据可视化,我们可以很直白的看到申请者是否被接收大致可以分为2类,分界还是很清晰的,我们可以试着手动画一条直线将其分开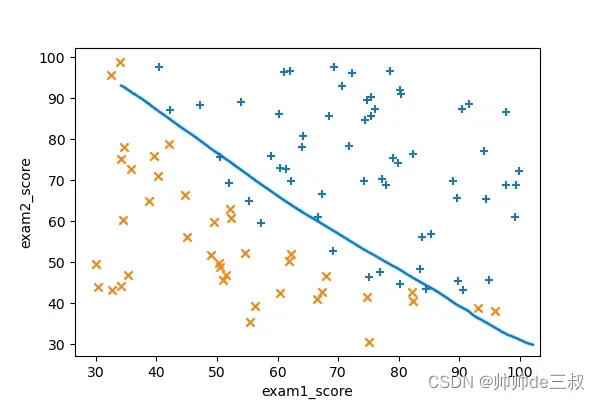
同时,我们可以利用前面的公式(1)把损失函数写出来
def cost(mytheta, myx, myy): #定义损失函数
return np.dot(-myy, np.log(np.exp(np.dot(myx, mytheta))/(1+np.exp(np.dot(myx, mytheta)))))+\
-np.dot((1-myy), np.log(1-np.exp(np.dot(myx, mytheta))/(1+np.exp(np.dot(myx, mytheta)))))
损失函数里面的mytheta是我们要求解的参数,这时可以调用scipy.optimize模块中的fmin函数进行求解
def optima(mytheta, myx, myy): #求最优解参数
result = fmin(cost, x0 = mytheta, args = (myx, myy), maxiter = 500, full_output= True)
return result
假设我们找到的参数是,那么边界函数可以表示为
学过线性规划的同学知道,这条直线可以将一个平面一分为二,大于0的划分为一边,小于0的划分为另一边。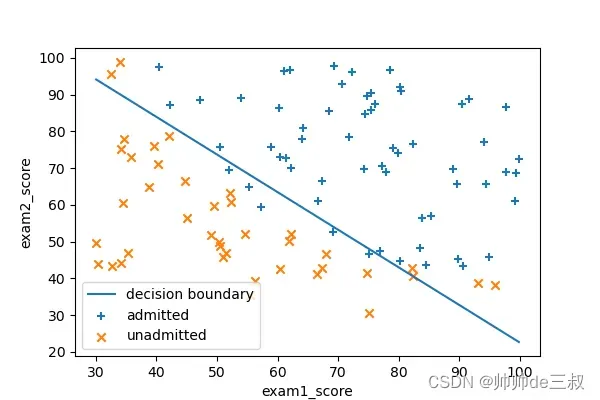
把边界函数的参数求解出来其实二项逻辑回归算法模型算是初步搭建完成了,因为这时候任给一个样本输入进来就可以判定其到底落于边界函数图形的左半边还是右半边。但一个优秀的算法模型不能仅仅做出来就算完事,还需要对其进行评估和优化,这时候混肴矩阵和ROC曲线就派上用场了。
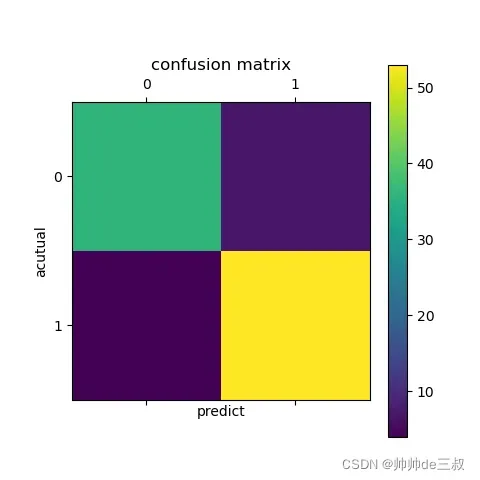
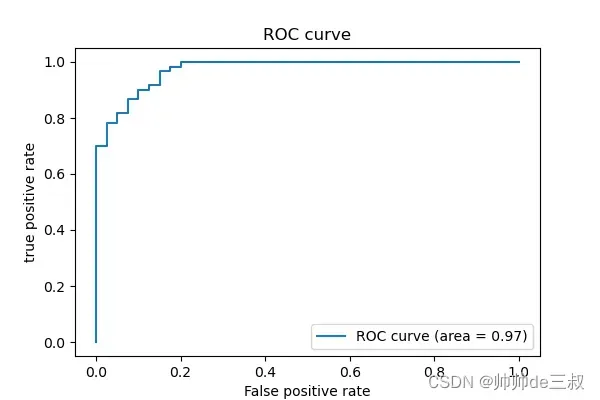
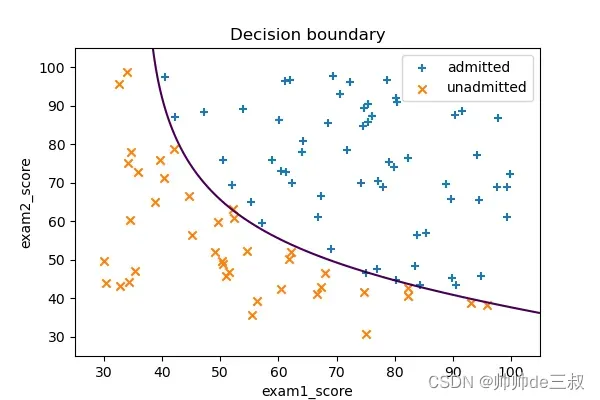
对比图7和图6,图7是通过数据学到的边界函数,而图6是我们随手画的分界线,两者有几分相似,说明通过逻辑回归算法模型达到我们最初的预期效果,也说明前期的数据可视化为我们提供很多有意义的线索,然而仔细观察图7,有些不被接收的点落入被接收的类里面,有些被接收的点落入不被接收的类里面,出现了串类,我们知道平面里两点确定一条直线,在这个实例中,显然利用直线作为分类边界肯定不能分干净,需要寻求曲线边界我们试着手动画一条曲线把中间那些容易混肴的点也尽可能的画到一边去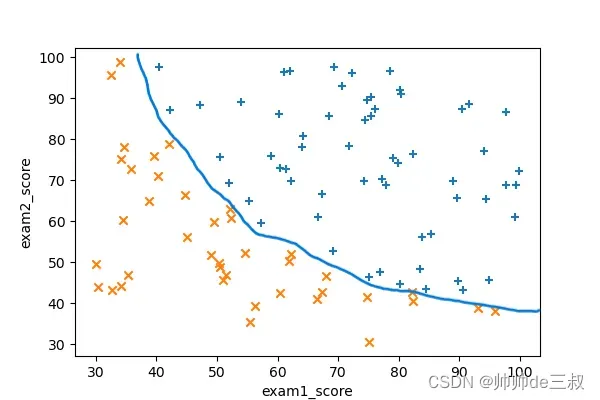
考虑到原始特征只有exam1_score和exam2_score2一共2个,为了后续表述方便起见,简记为,想要制作曲线边界可以考虑利用特征映射对特征进行扩充,具体做法是利用
生成
,因为更多的特征进行逻辑回归时,得到的边界曲线更具表现力。为了方便,我们设定其中的n=2,此时的决策函数如下,到时候求出来的参数也会有6个
这时候有读者就会问,你这由原来2个特征一下构造出来5个特征,结果还能可视化吗?高维空间直接可视化肯定是不行的,但是可以将高维的曲面投影到二维平面画出其对应的等值线。
def project(mytheta): #特征映射后投影边界
plt.figure(figsize=(6, 4))
visualization()
xs = np.linspace(25, 105, 100)
ys = np.linspace(25, 105, 100)
zs = np.zeros((len(xs), len(ys)))
for i in range(len(xs)):
for j in range(len(ys)):
fij = fmap(np.array([xs[i]]), np.array([ys[j]]))
zs[i][j] = np.dot(fij, mytheta)
zs = zs.transpose()
u, v = np.meshgrid(xs, ys)
plt.contour(xs, ys, zs, [0])
plt.title("Decision boundary")
plt.pause(5)
至此,关于逻辑回归算法模型我们除了正则化没讨论外几乎该讨论的都讨论了,其中在算法模型评估环节涉及到混肴矩阵,ROC曲线等概念后面我们会专门出一期博文,敬请期待。
所有代码
# -*- encoding: utf-8 -*-
'''
@Project : logistic_regression
@Desc : 利用逻辑回归算法模型预测学生是否会被接收
@Time : 2022/03/26 13:43:53
@Author : 帅帅de三叔,zengbowengood@163.com
'''
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.optimize import fmin
from sklearn.metrics import confusion_matrix
from sklearn.metrics import roc_curve, auc
data = pd.read_csv("D:\项目\机器学习\吴恩达机器学习课件\CourseraML\ex2\data\ex2data1.txt", header = None, names=["exam1_score", "exam2_score", "label"]) #读取数据
X = np.array(data[["exam1_score", "exam2_score"]]) #自变量
y = data["label"] #因变量
X = np.insert(X, 0, 1, axis = 1) #插入虚拟变量,纳入常数项
m = len(data) #样本量
pos = np.array([X[i] for i in range(len(X)) if y[i]==1]) #正性特征
neg = np.array([X[i] for i in range(len(X)) if y[i]==0]) #负性特征
def visualization(): #可视化
#plt.figure(figsize = (6,4)) #新建画布
plt.scatter(pos[:,1], pos[:, 2], marker='+', label='admitted') #正性散点
plt.scatter(neg[:,1], neg[:,2], marker='x', label = 'unadmitted') #负性散点
plt.xlabel("exam1_score")
plt.ylabel("exam2_score")
plt.legend()
plt.pause(2)
def cost(mytheta, myx, myy): #损失函数
return np.dot(-myy, np.log(np.exp(np.dot(myx, mytheta))/(1+np.exp(np.dot(myx, mytheta)))))+\
-np.dot((1-myy), np.log(1-np.exp(np.dot(myx, mytheta))/(1+np.exp(np.dot(myx, mytheta)))))
def optima(mytheta, myx, myy): #求最优解
result = fmin(cost, x0 = mytheta, args = (myx, myy), maxiter = 500, full_output= True)
return result
def boundary(mytheta, myx): #边界函数
xs = np.array([np.min(myx[:,1]), np.max(myx[:,1])]) #横坐标2个点
ys = -(mytheta[0][0] + mytheta[0][1]*xs)/mytheta[0][2] #纵坐标2个点
plt.plot(xs, ys, label = 'decision boundary') #决策边界
plt.xlabel("exam1_score")
plt.ylabel("exam2_score")
plt.legend()
plt.pause(2)
def descision(mytheta, myx): #决策函数
y_score = np.dot(X, mytheta) #概率得分(0~1)
y_pred = np.zeros(len(myx)) #用来存预测值(0,1)
for i in range(len(myx)):
if np.dot(mytheta, myx[i, :]) >=0.5:
y_pred[i] = 1
else:
y_pred[i] = 0
return y_score, y_pred
def conf_matrix(y_pred, y_true): #混肴矩阵
tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel() #
plt.matshow([[tn, fp], [fn, tp]])
plt.title("confusion matrix")
plt.xlabel("predict")
plt.ylabel("acutual")
plt.colorbar()
plt.pause(2)
def roc(y_true, y_pred): #绘制roc曲线
plt.figure(figsize = (6,4)) #新建画布
fpr, tpr, thresholds = roc_curve(np.array(y_true), np.array(y_pred))
auc_ = auc(fpr, tpr)
plt.plot(fpr, tpr, label = "ROC curve (area = %0.2f)"%auc_)
plt.xlabel("False positive rate")
plt.ylabel("true positive rate")
plt.title("ROC curve")
plt.legend()
plt.pause(2)
def fmap(x1, x2): #特征映射
n = 2 #最高阶
out = np.ones((x1.shape[0], 1)) #100*1的向量
for i in range(1, n+1):
for j in range(0, i+1):
term1 = x1**(i-j)
term2 = x2**(j)
term = (term1*term2).reshape(term1.shape[0], 1)
out = np.hstack((out, term)) #水平平铺
return out
def project(mytheta): #特征映射后投影边界
plt.figure(figsize=(6, 4))
visualization() #把原来散点也画进来观察效果
xs = np.linspace(25, 105, 100)
ys = np.linspace(25, 105, 100)
zs = np.zeros((len(xs), len(ys)))
for i in range(len(xs)):
for j in range(len(ys)):
fij = fmap(np.array([xs[i]]), np.array([ys[j]])) #调用特征映射
zs[i][j] = np.dot(fij, mytheta)
zs = zs.transpose()
u, v = np.meshgrid(xs, ys)
plt.contour(xs, ys, zs, [0]) #等值线
plt.title("Decision boundary")
plt.pause(5)
if __name__=="__main__":
visualization() #原数据可视化
inital_theta = np.zeros((X.shape[1], 1)) #参数初始化,3*1的零向量
result = optima(inital_theta, X, y) #参数,当前函数值,迭代次数和function evaluation
boundary(result, X) #画出决策边界
y_score, y_pred = descision(result[0], X) #预测值
conf_matrix(y, y_pred) #混肴矩阵
#roc(y,y_pred) #ROC曲线
roc(y, y_score) #ROC曲线
X_map = fmap(X[:,1], X[:,2]) #特征映射
initial_theta_map = np.zeros((X_map.shape[1], 1))
result_map = optima(initial_theta_map, X_map, y) ##参数,当前函数值
project(result_map[0])
参考
1,对数函数
2,python绘制对数函数
3,如何理解logistic函数
4,logit究竟是个啥?
5,逻辑回归
6,从原理到代码,轻松深入逻辑回归
7,https://www.zybuluo.com/frank-shaw/note/143260
8,混肴矩阵
文章出处登录后可见!
