前置知识

如果你对偏导数、方向导数和梯度的概念不是很清楚，欢迎考古：为什么梯度方向是函数增加最快的方向。

实施过程

梯度下降法也叫做梯度下山法，充分补充了前置知识后，然后在理解梯度下降法，会很简单。梯度是所有偏导数组成的Vector，一个点梯度的方向是函数在这个点增加速度最快的方向（具体证明方法在上面已经展示）。
公式如下：

其中a代表学习率，也就是步长。他代表更新参数时候的步幅迈多大。
重复以上操作，直到不再变化。这里要注意，这两个参数是同时更新的。如果先改变第一个参数，然后使用包含第一个更新参数的函数更新参数，最终的结果会与梯度下降法存在偏差。
我面我们用一个简单地用梯度下降法来优化函数在（6，-6）点地参数，来证明梯度下降法。我们可以看出当参数在（0,0）的时候为最小值。
假设a=0.5


我们发现经过一次优化后，的原点更近了一步，使得参数最终可以到达原点（假设函数是凸的）。
求一个点在一维上的偏导数。如果结果是正的，那么这个维度在这一点上是一个递增函数。反之，相反，我们知道增加和减少，我们知道函数往哪个方向走。函数的值达到最小值。

沿着梯度减小的方向走，梯度会越来越小，我们步长就会越来越小，到达极值点后，梯度达到水平，梯度值接近0，更新的参数也就不再变化。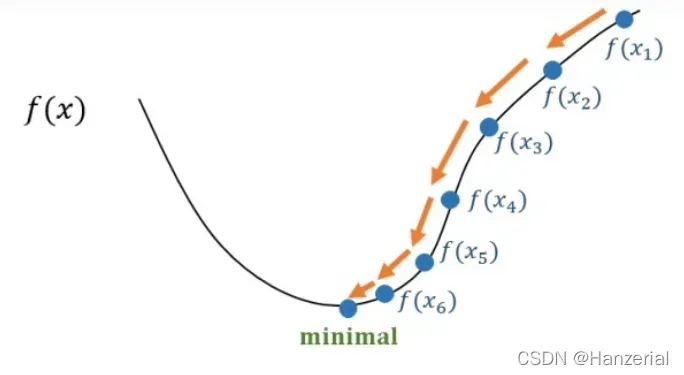

局限性

学习率

学习率的选择比较苛刻，不能太大也不能太小。如果太大，更新参数时可能会直接跳过极值点，导致梯度越来越大，最后爆炸。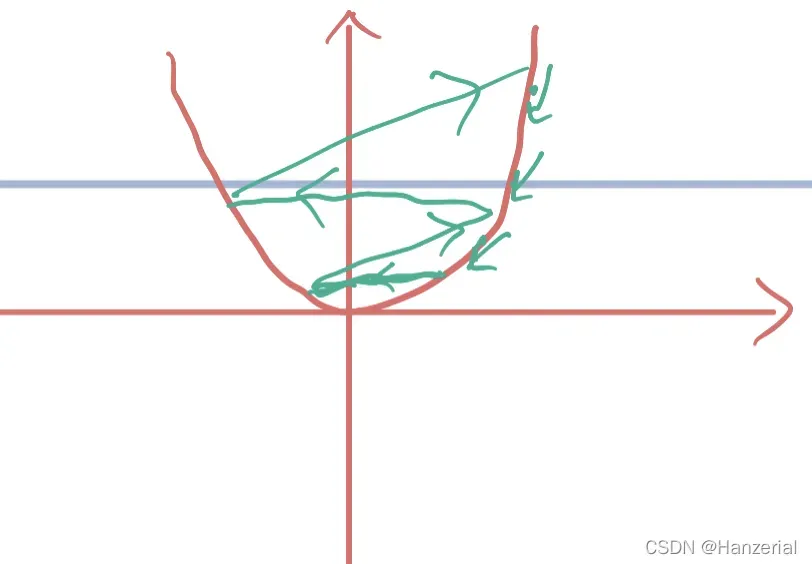

如果学习率太小，学习率就会太慢。
在做梯度下降法之前，需要对函数进行归一化。如果不进行归一化操作，函数找到极值的时间会大大增加，如图：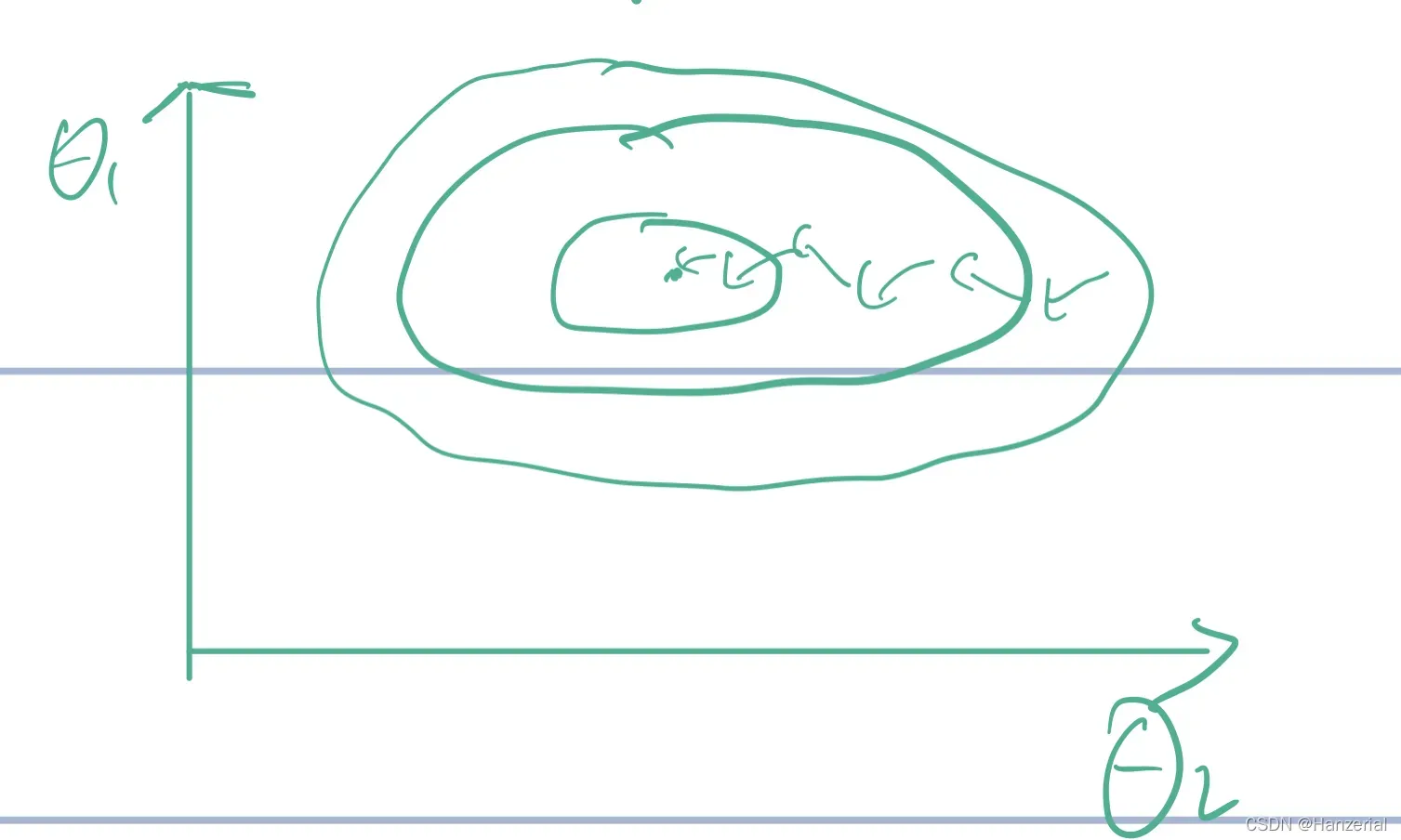
当参数的范围相差不大时，轮廓图像会更接近一个圆，找到最优解所需的时间会大大减少。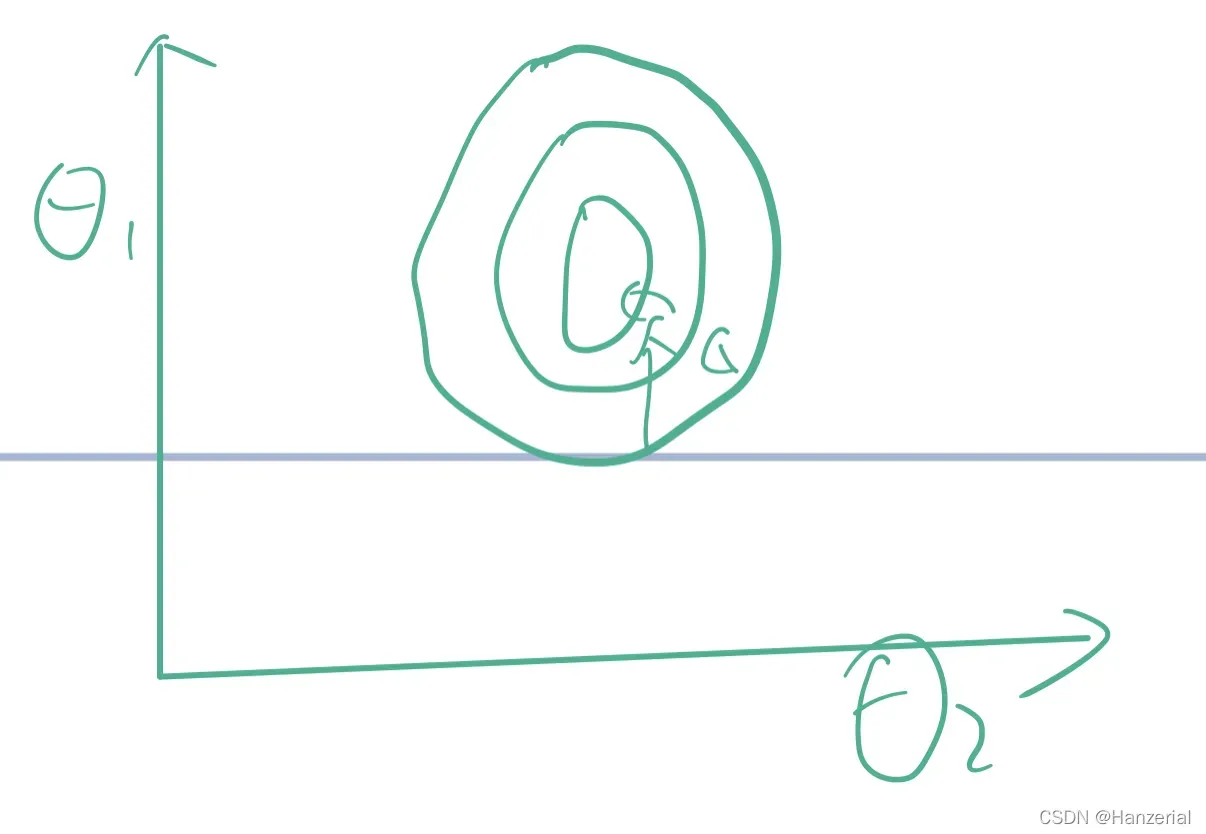

初始点

选择起点尤为重要。如果代价函数是一个（非凸函数），那么它的极值点不是唯一的，最终的迭代结果可能是函数的局部最优解。