使用 PyMC3 进行贝叶斯客户生命周期价值建模
实现 BG-NBD,一种概率层次模型,使用 PyMC3 分析客户购买行为

客户生命周期价值 (CLV) 是客户在其关系期间对公司的总价值。公司客户群的集体 CLV 反映了其经济价值,并且经常被衡量以评估其未来前景。
虽然存在许多估算 CLV 的方法,但在过去几十年中出现的最有影响力的模型之一是 Beta 几何负二项分布 (BG-NBD)。¹该框架使用 Gamma 和 Beta 模拟客户的重复购买行为分布。本系列文章的第 1 部分已经探讨了该模型背后的数学原理。同时,第 2 部分介绍了生命周期,该库允许我们方便地拟合 BG-NBD 模型并获得其最大似然估计 (MLE) 参数。如果您还没有阅读这些部分,我建议您阅读这些部分,因为即将发布的内容建立在它们之上。[0][1][2][3][4]
本系列的最后一部分介绍了实现 BG-NBD 的另一种方法——一种依赖于贝叶斯原理的方法。我们将使用 PyMC3 来编写这个实现。虽然本文的主要目的是通过贝叶斯镜头阐明 BG-NBD,但也将介绍贝叶斯世界观和 PyMC3 框架的一些一般观点。这是我们的议程:[0]
- 首先,我们将争辩说贝叶斯实现比常客提供了一些优势。
- 其次,我们将提供一个实现“蓝图”来指导我们的编码步骤。
- 第三,我们将花一些时间研究先前的选择——贝叶斯建模中的一个关键组成部分。
- 接下来,我们将介绍 PyMC3 代码及其复杂性,包括著名的蒙特卡洛马尔可夫链 (MCMC) 算法。
- 最后,我们将分析贝叶斯 BG-NBD 模型的输出,并将其与生命周期的输出进行比较。
让我们开始吧!
为什么是贝叶斯?
您可能想知道,如果我们的武器库中已经有了用户友好的生命周期,为什么还需要另一个实现。答案在于频率论和贝叶斯推理之间的对比以及后者提供的优势。
为了说明这些差异,让我们将常客和贝叶斯框架想象成两个试图对统计问题(例如 CLV 估计)建模的编程函数。我们将看到这些函数在输入和输出方面存在重大差异。
这两个函数都将数据集(观察)作为输入。但是,贝叶斯函数需要先验分布形式的额外输入。先验反映了我们对模型参数的初始假设,并将在考虑到观察结果后进行更新。
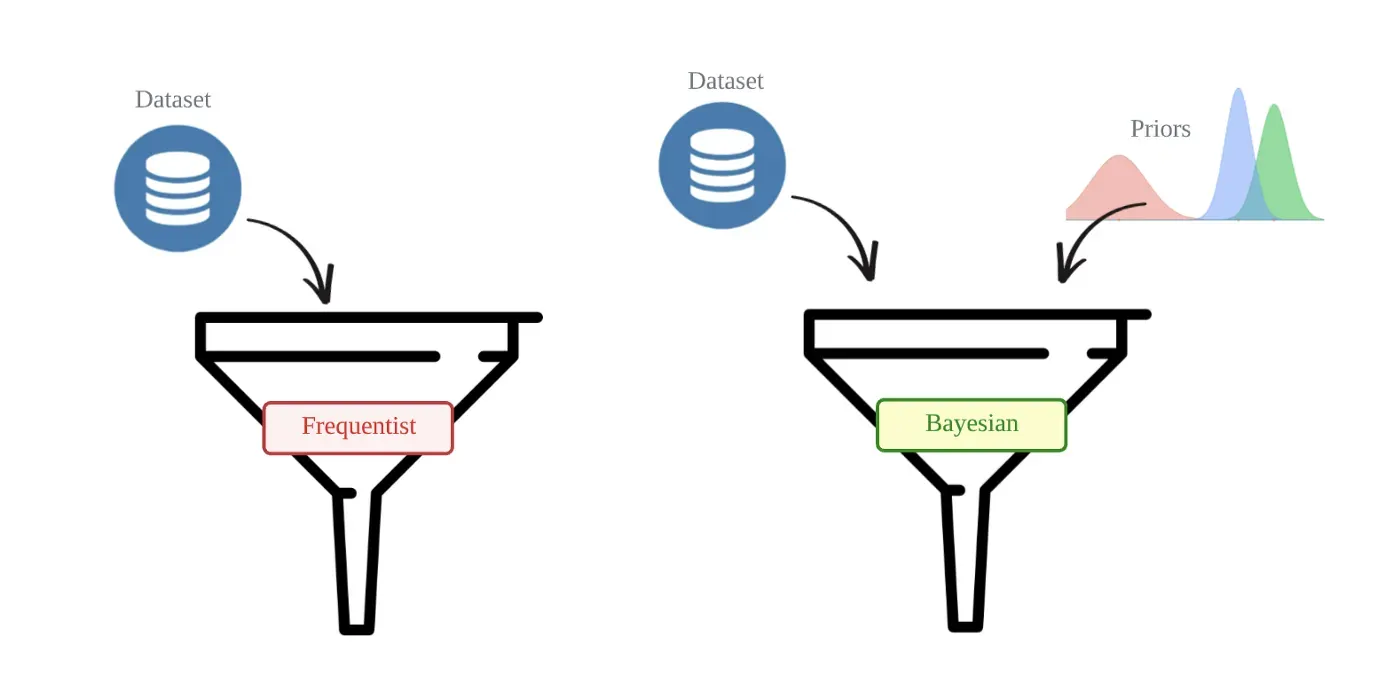
包含先验是一把双刃剑。一方面,先验为用户提供了一种使用他们的领域知识来“引导”模型找到正确参数的方法。例如,在 BG-NBD 中,如果我们确定我们的大多数客户以每周 4 次交易的速率 λ 进行购买,我们可以提供导致平均为 4 的 Gamma 分布的先验。如果这种直觉是只是稍微偏离标准(例如,如果实际 λ 是 3.5 次交易/周),贝叶斯框架将允许我们仅用很少的数据点得出正确的值。
另一方面,由于没有单一的“正确”方法来选择先验,贝叶斯建模过程是主观的和可变的。两位统计学家共享相同的数据但使用不同的先验结果可能最终会得到完全不同的结果。这种主观性是一些从业者避开贝叶斯的主要原因之一。然而,随着建模中包含更多数据点,先验的影响会减弱。
这两个函数的输出也不同。它们都返回模型的参数估计,但形式不同。常客将它们作为点估计返回。例如,我们已经看到频率库生命周期如何使用 MLE 来计算 r、α、a 和 b 的点估计。相反,贝叶斯将它们作为概率分布返回。这些分布,称为后验,代表我们在考虑观察后对参数的更新信念。[0]
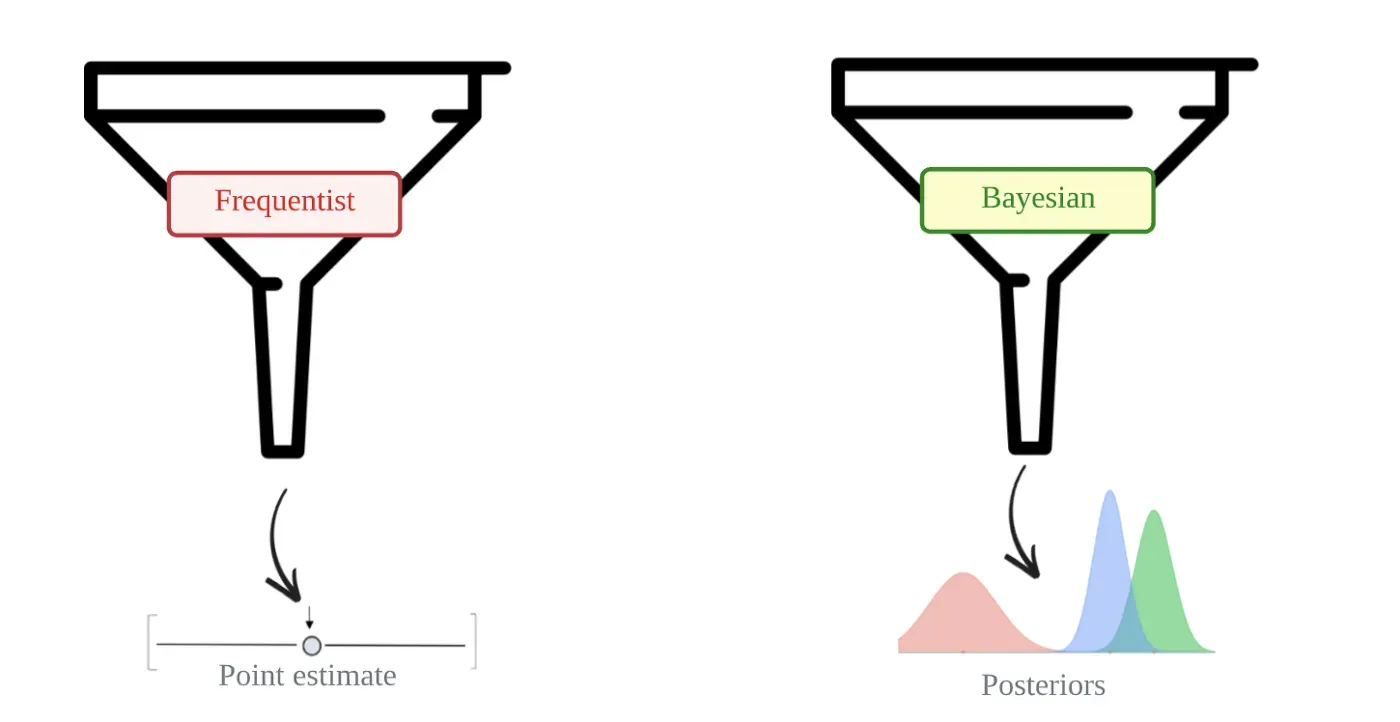
获得后验是贝叶斯框架胜过常客的另一个方面。使用后验,很容易可视化参数的最合理值并量化我们估计中的任何不确定性。此外,如果有额外的观察结果可用,前后循环提供了一种更新参数的原则方法。
实施蓝图
我们在第 1 部分中看到 BG-NBD 模型是一个分层概率模型。这里的分层是指某些分布的参数由其他分布(“父”分布)建模的事实。我们很快就会看到 PyMC3 允许我们在代码中表达这些父子关系。
下面提供了一个蓝图来指导编码步骤。此蓝图遍历模型的逻辑流程,从其输入(数据和先验分布)开始,到其输出(后验分布)结束。
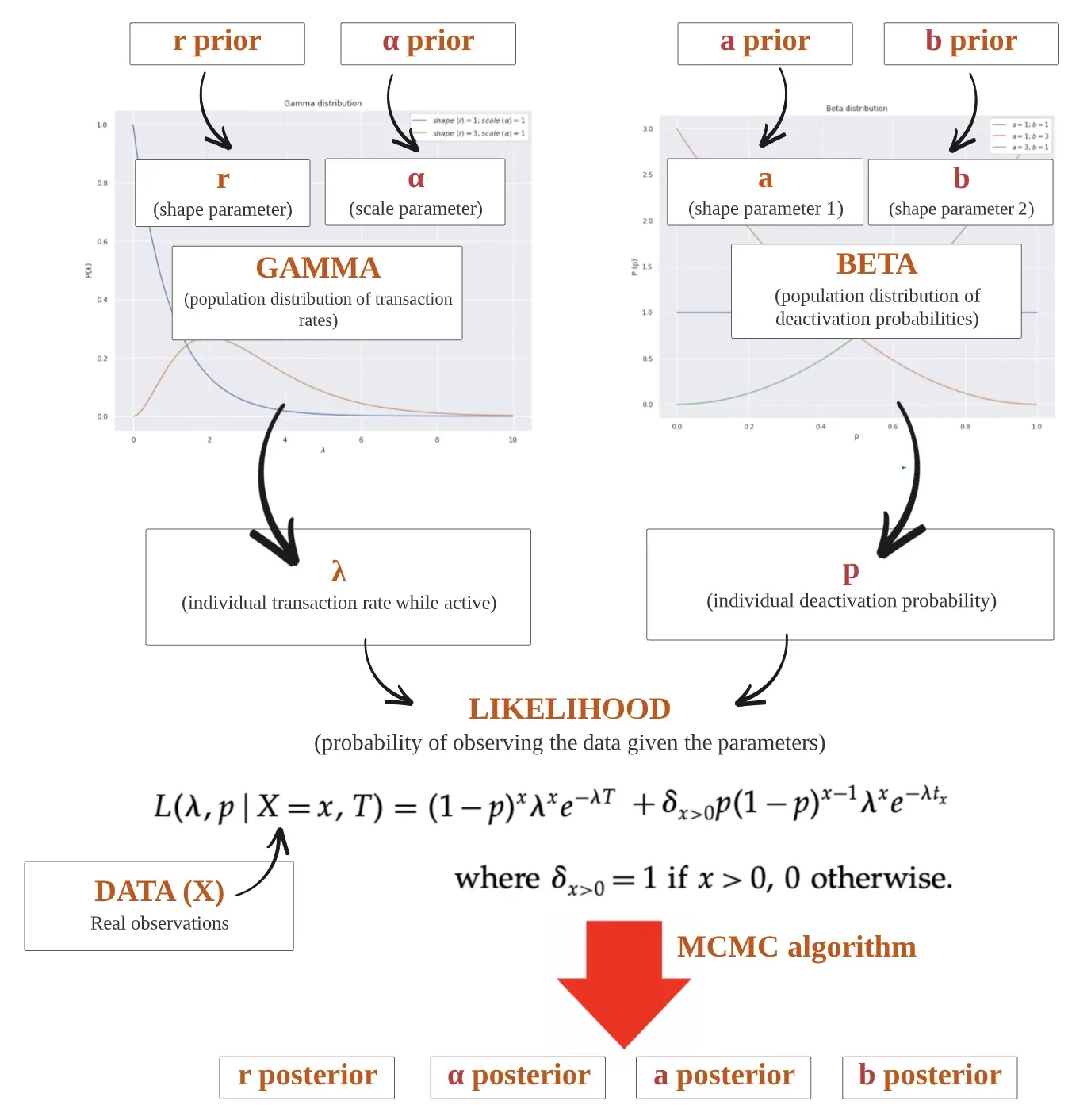
对上述蓝图的一些说明:
- Gamma 分布表示交易率 λ 在客户群体中的分布。它由两个参数参数化:r 和 α。我们将为 r 和 α 提供先验,这些先验将通过我们的观察进行更新。
- Beta 分布表示客户群体中停用概率 p 的分布。它由两个形状参数参数化:a 和 b。同样,我们将为这些参数提供先验。
- 来自 Gamma 分布的 λ 和来自 Beta 分布的 p 有助于似然函数,它表示观察数据集中交易的概率。这种可能性是绑定我们的数据和我们的理论的方程式。
- PyMC3 中的 MCMC 算法将使我们能够对 r、α、a 和 b 的后验分布进行采样。我们稍后会更多地讨论这个算法。
第 1 部分提供了有关上述分配的详细信息;如果您不熟悉它们,请查看它![0]
先验的选择
Consideration
如前所述,我们需要为 r、α、a 和 b 分别提供先验。我们可以将这些先验及其各自的参数视为我们模型的“超参数”。选择先验时需要牢记各种注意事项:
- 先验可以根据现有知识制定,而现有知识又可以来自领域专业知识、历史观察或过去的建模实验。
- 当没有可用信息时,可以选择无信息先验来反映可能参数值之间的差异。
- 我们可以施加一些约束来指导我们的选择。例如,我们可以要求我们的先验分布是对称的、严格正的、重尾分布等。
在我们的案例中,以下是我们的考虑和假设:
- 至于购买率 λ,我们假设我们有强烈的直觉,我们的大部分客户以每周 4 次购买的速度进行交易。我们将选择反映这种先验信念的 Gamma 先验。
- 相反,我们假设没有关于我们客户的停用概率 (p) 的先验知识。因此,我们将选择信息量不足的 Beta 先验。
- 因为我们所有的参数(r、α、a 和 b)只能是正实数,所以我们选择的先验分布必须为负数分配零概率密度。
截断正态分布
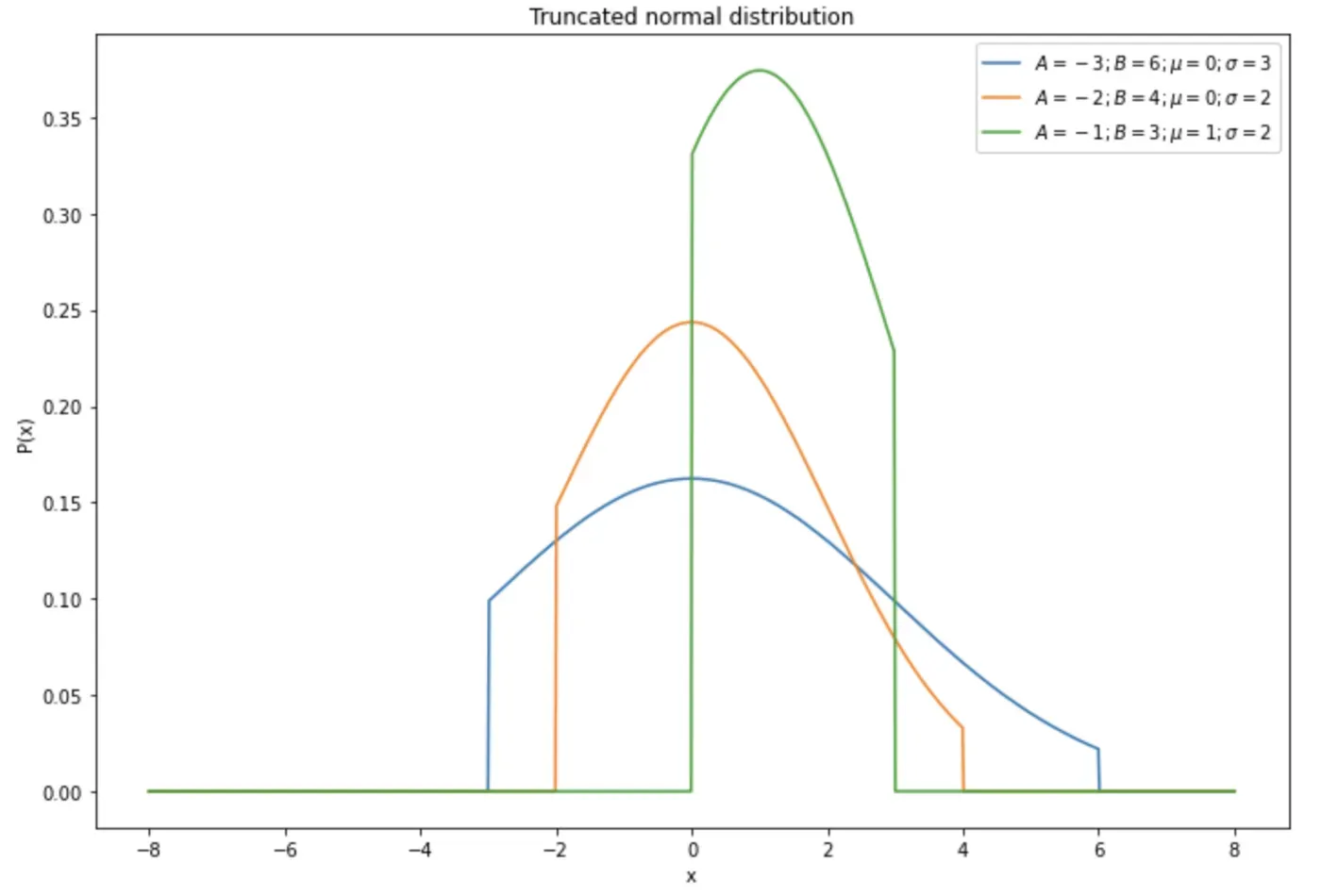
先验的一个很好的候选是截断正态分布。顾名思义,截断正态分布是被“截断”的高斯分布。也就是说,它的密度超出指定的左和右极限被设置为零,并且极限之间的密度被重新归一化为总和为 1。分布有四个参数:左右极限(通常称为 A 和B)、均值 μ 和标准差 σ。[0]
截断法线经常被用作先验,因为它的四个参数提供了一种直观的方式来“猜测”一个值。 μ 代表我们最可能的猜测,σ 反映我们的不确定性水平,A 和 B 分别指定下限和上限约束。
以下是截断法线的一些示例:
伽玛和贝塔先验
考虑到这些因素,现在让我们构建我们的 Gamma 先验。以下是步骤:
1. 如前所述,我们有一个先验信念,即 Gamma 分布的最可能值(即其平均值)是 4 次交易/周。
2. 然后我们选择 Gamma 参数 r 和 α 的特定组合,从而得到所需平均值为 4 的 Gamma 分布。我们知道 Gamma 分布的平均值可以通过简单的公式 μ = rα 计算;因此,可以选择乘积为 4 的任何一对正数作为 r 和 α 的候选者。让我们将 r 设置为 8,将 α 设置为 0.5。使用这些参数构建的 Gamma 分布如下图所示:[0]
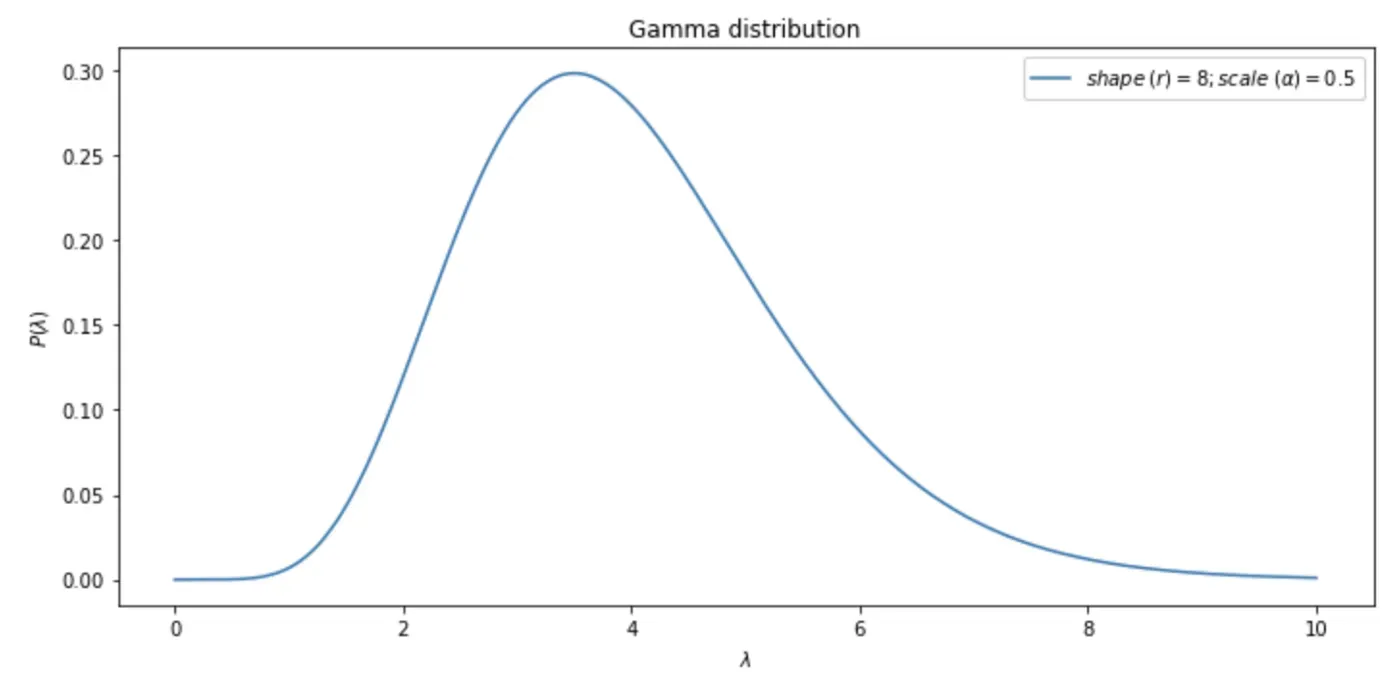
3. 这些 r 和 α 值代表我们最初的猜测。由于我们不能 100% 确定这些猜测,我们应该将它们呈现为分布而不是点估计。我们将这些分布称为先验。由于前面提到的原因,我们将使用截断法线来表示这些先验。
4. 现在让我们关注 r。 r 的截断法线将具有以下参数:
- μ:8(我们最可能的初始猜测)
- σ:7(一个相当宽的标准偏差,反映了我们的高不确定性水平)
- A:0(因为我们知道 r 不能为负)
- B:40(这里,我们选择一个我们不会超过的极右极限)。
使用这些参数构建的截断法线如下图所示:
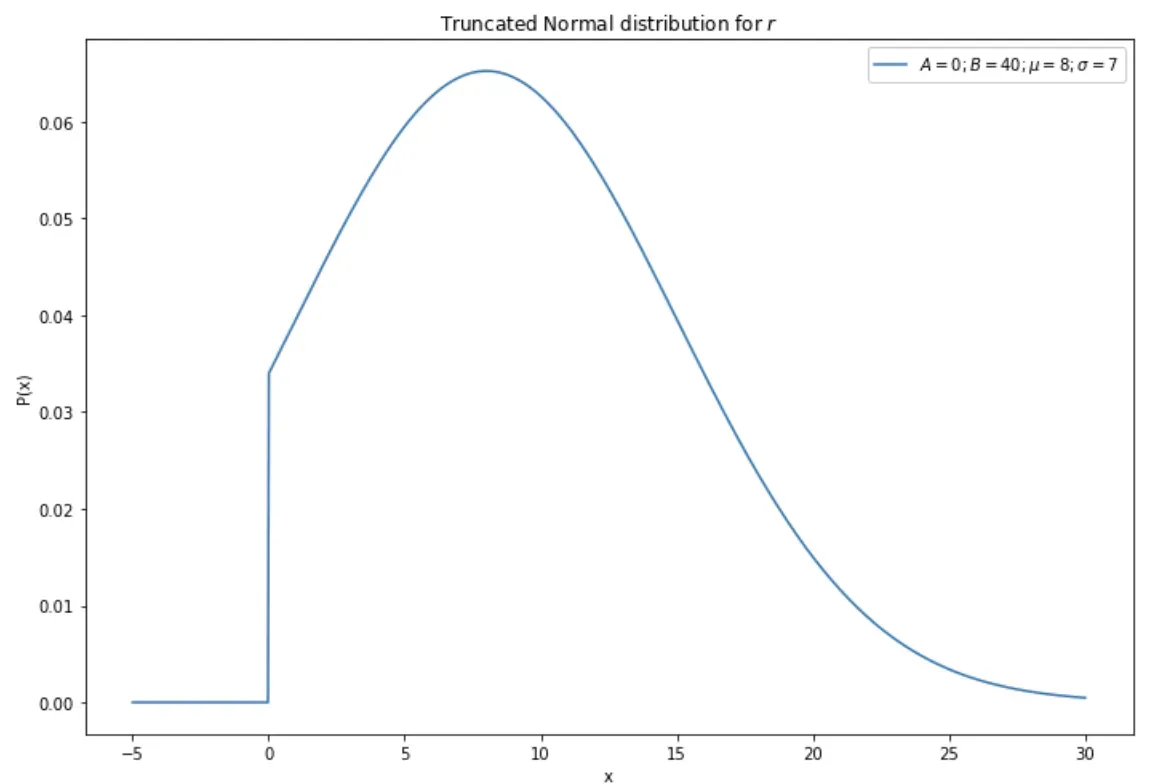
5. 重复上述过程,得到α、a、b的先验。工作流程如下图所示:
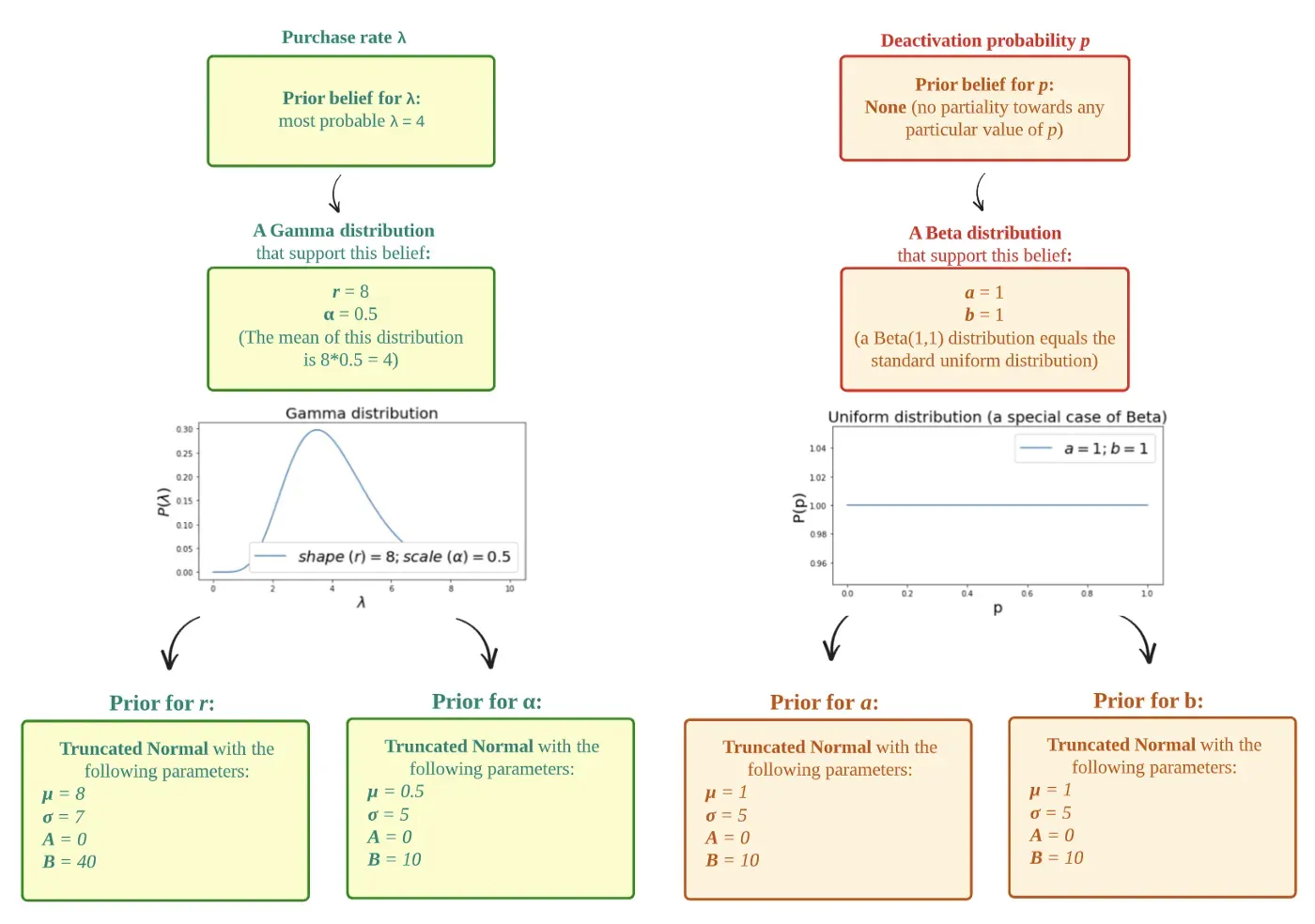
请注意,对于 Beta 参数 a 和 b,我们选择了无信息的均匀分布作为先验,以反映我们对客户的停用概率 (p) 没有先验知识。
在 PyMC3 中编码一切
Dataset
在本文中,我们将使用生命周期提供的示例数据集(MIT 许可)。此表记录了 CDNow 的交易,这是一家销售 CD 的 dot-com 时代公司。这是我们加载它的方式:[0][1]
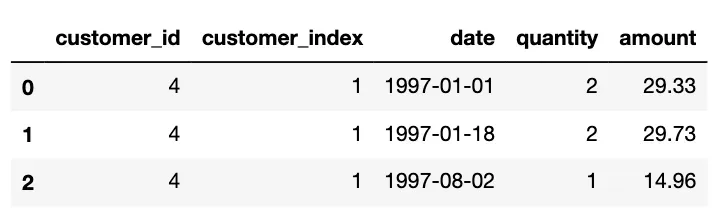
正如第 2 部分中所讨论的,在建模之前,此事务表应经过两个先决步骤:[0]
- 转换为规范的“RFM”格式,以及
- 分为校准集和保持集。
我们将使用我们在第 2 部分中使用的相同拆分机制来促进寿命和 PyMC3 估计值之间的比较。

PyMC3 在行动
建立了这个理论框架后,我们现在可以开始编码了。我们将使用 PyMC3,一个强大的贝叶斯建模库。虽然我们将提供一些关于 PyMC3 本身的提示,但我们的重点将放在 BG-NBD 实施²上。
在 PyMC3 中,概率模型由 pm.Model() 对象表示,该对象通常编码为上下文管理器。此模型将包含由 Distribution 对象表示的多个分布。这些分布对象之间可以有父子关系,其中父对象的值影响/确定子对象的值。
以下是 PyMC3 中的 BG-NBD 实现。如您所见,代码与前面介绍的理论非常相似。
from pymc3.math import log, exp, where
import pymc3 as pm
import numpy as np
# We use the "calibration" portion of the dataset to train the model
N = rfm_cal_holdout.shape[0] # number of customers
x = rfm_cal_holdout['frequency_cal'].values # repeat purchase frequency
t_x = rfm_cal_holdout['recency_cal'].values # recency
T = rfm_cal_holdout['T_cal'].values # time since first purchase (T)
# Modeling step
bgnbd_model = pm.Model()
with bgnbd_model:
# Priors for r and alpha, the two Gamma parameters
r = pm.TruncatedNormal('r', mu=8, sigma=7, lower=0, upper=40)
alpha = pm.TruncatedNormal('alpha', mu=0.5, sigma=5, lower=0, upper=10)
# Priors for a and b, the two Beta parameters
a = pm.TruncatedNormal('a', mu=1, sigma=5, lower=0, upper=10)
b = pm.TruncatedNormal('b', mu=1, sigma=5, lower=0, upper=10)
# lambda_ (purchase rate) is modeled by Gamma, which is a child distribution of r and alpha
lambda_ = pm.Gamma('lambda', alpha=r, beta=alpha, shape=N, testval=np.random.rand(N))
# p (dropout probability) is modeled by Beta, which is a child distribution of a and b
p = pm.Beta('p', alpha=a, beta=b, shape=N, testval=np.random.rand(N))
def logp(x, t_x, T):
"""
Loglikelihood function
"""
delta_x = where(x>0, 1, 0)
A1 = x*log(1-p) + x*log(lambda_) - lambda_*T
A2 = (log(p) + (x-1)*log(1-p) + x*log(lambda_) - lambda_*t_x)
A3 = log(exp(A1) + delta_x * exp(A2))
return A3
# Custom distribution for BG-NBD likelihood function
loglikelihood = pm.DensityDist("loglikelihood", logp, observed={'x': x, 't_x': t_x, 'T': T})
# Sampling step
SEED = 8
SAMPLE_KWARGS = {
'chains': 1,
'draws': 4000,
'tune': 1000,
'target_accept': 0.7,
'random_seed': [
SEED,
]
}
with bgnbd_model:
trace = pm.sample(**SAMPLE_KWARGS)
# It's a good practice to burn (discard) early samples
# these are likely to be obtained before convergence
# they aren't representative of our posteriors.
trace_trunc = trace[3000:]话虽如此,代码的两个部分可能并不那么简单,值得进一步讨论。这些部分,自定义似然函数(第 30-41 行)和 MCMC 采样(第 43-62 行),将在下面详细说明。
自定义似然函数
PyMC3 配备了许多 Distribution 对象,每个对象都对应于众所周知的概率分布,例如 Beta 或 Gamma 分布。但是,当涉及非标准概率分布(例如 BG-NBD 似然函数)时,需要自定义实现。
提醒一下,BG-NBD 模型中的似然函数如下所示(其推导在第 1 部分中提供):[0]

您可能记得在您的统计课中,最大似然估计 (MLE) 涉及在我们的整个数据集上乘以似然函数的输出。由于这些乘法步骤中的每一个都输出一个分数,因此直接计算似然性可能会导致浮点问题。为了避免这种情况,习惯上将似然函数转换为对数似然函数,这样更便于优化。上述函数的对数似然版本如下:
我们在 logp 函数中实现的正是上述公式。然后,我们通过实例化一个新的 DensityDist 对象并在实例化期间传递可调用对象,将此函数转换为 Distribution 对象。因为这个 Distribution 对象的值是已知的,所以我们还在其实例化期间提供了这些已知值(来自我们的数据的 x、tₓ 和 T)。[0]
MCMC算法
在描述了模型之后,我们可以执行一个 MCMC 算法来采样后验分布。 MCMC 是一系列模拟算法,允许从其封闭式 PDF 或 PMF 未知的分布中进行采样。它通过构建马尔可夫链来工作——一个多状态系统,允许根据特定的概率规则从一个状态转换到另一个状态。该链的设计使其稳定状态与要采样的分布相匹配。

我们使用 pm.sample() 开始链构建和采样。完成后,该函数返回一个包含所绘制样本的跟踪对象。如果采样过程顺利(即达到稳定状态),这些样本将代表我们想要的后验。
在进一步分析之前,我们应该确认算法的收敛性(达到稳态),因为使用收敛前获得的样本可能会导致错误的下游分析。为了确定收敛,我们可以使用 pm.trace_plot()⁴ 绘制轨迹; “蜿蜒”模式表示不收敛,不是 bueno。[0]
这是我们实验的轨迹图:
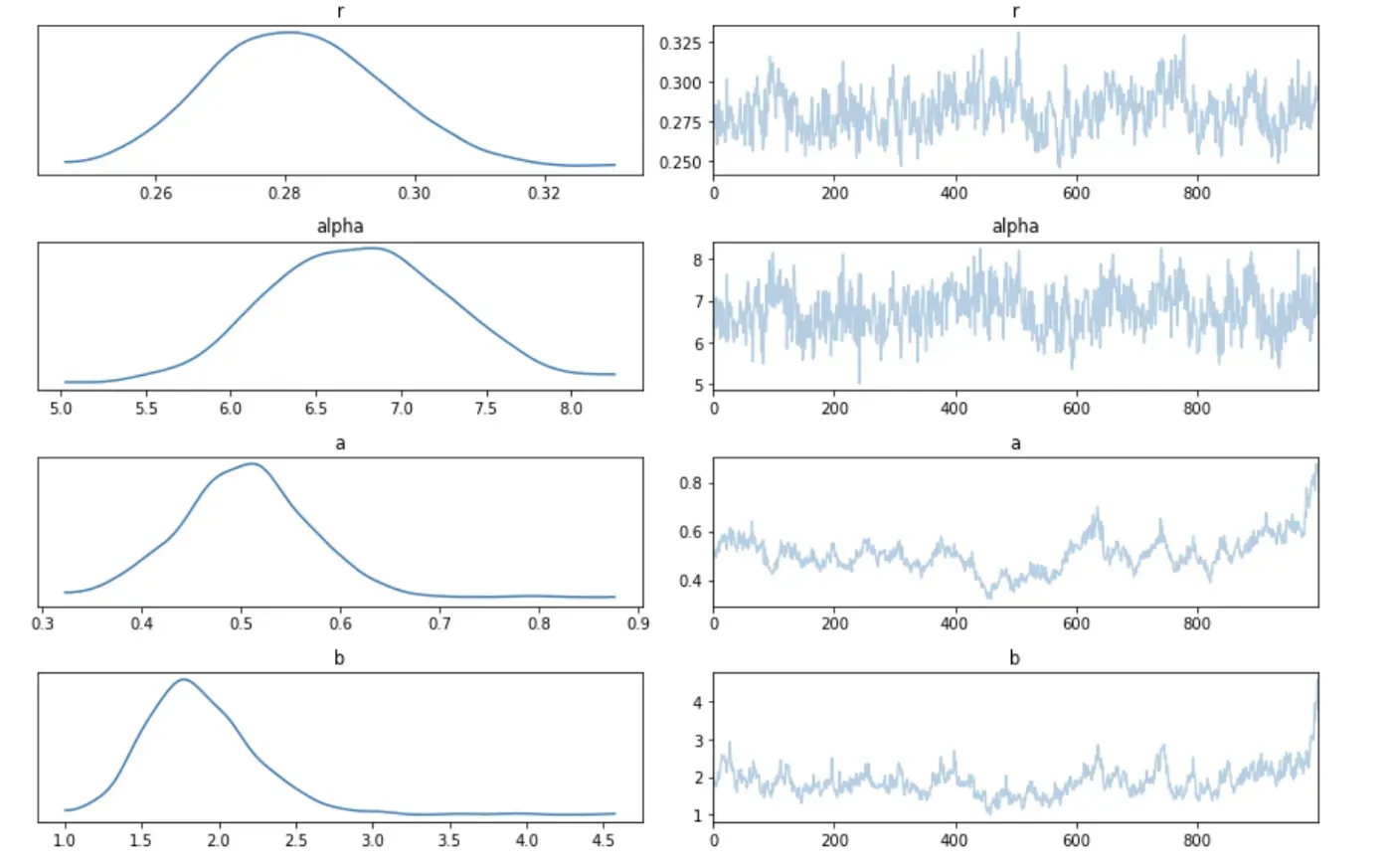
我们看到没有检测到明显的不收敛迹象。
后验分布分析
先验与后验
由于我们确信采样过程运行正常,我们可以继续分析后验。一个常见的起点是 pm.summary(),它返回我们后验的汇总统计信息。让我们打印他们的手段。
params_mean = pm.summary(trace_trunc, var_names = ["r", "alpha", "a", "b"])["mean"]
params_mean
我们注意到,这些后验均值与先前均值完全不同。例如,b 从 1(先验均值)变为 2.736(后验均值)。这表明我们先前的信念没有得到数据的完全支持,因此被“更新”了。
与生命周期输出的比较
在本系列的上一篇文章中,我们已经看到使用生命周期库也可以用来估计参数 r、α、a 和 b。现在让我们比较两个实现的结果:
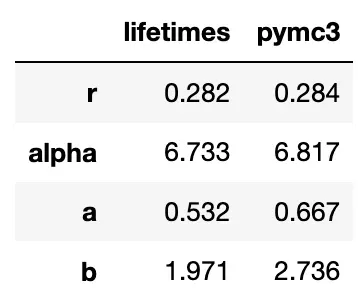
我们看到,尽管来自不同的框架(frequentist vs Bayesian),但估计的参数并没有那么不同。
分析估计的 Beta 和 Gamma 分布
然后,我们可以使用贝叶斯后验的均值(即最可能的)参数值来构建和可视化 Gamma 和 Beta 分布。
让我们从 Gamma 开始——这是图表:
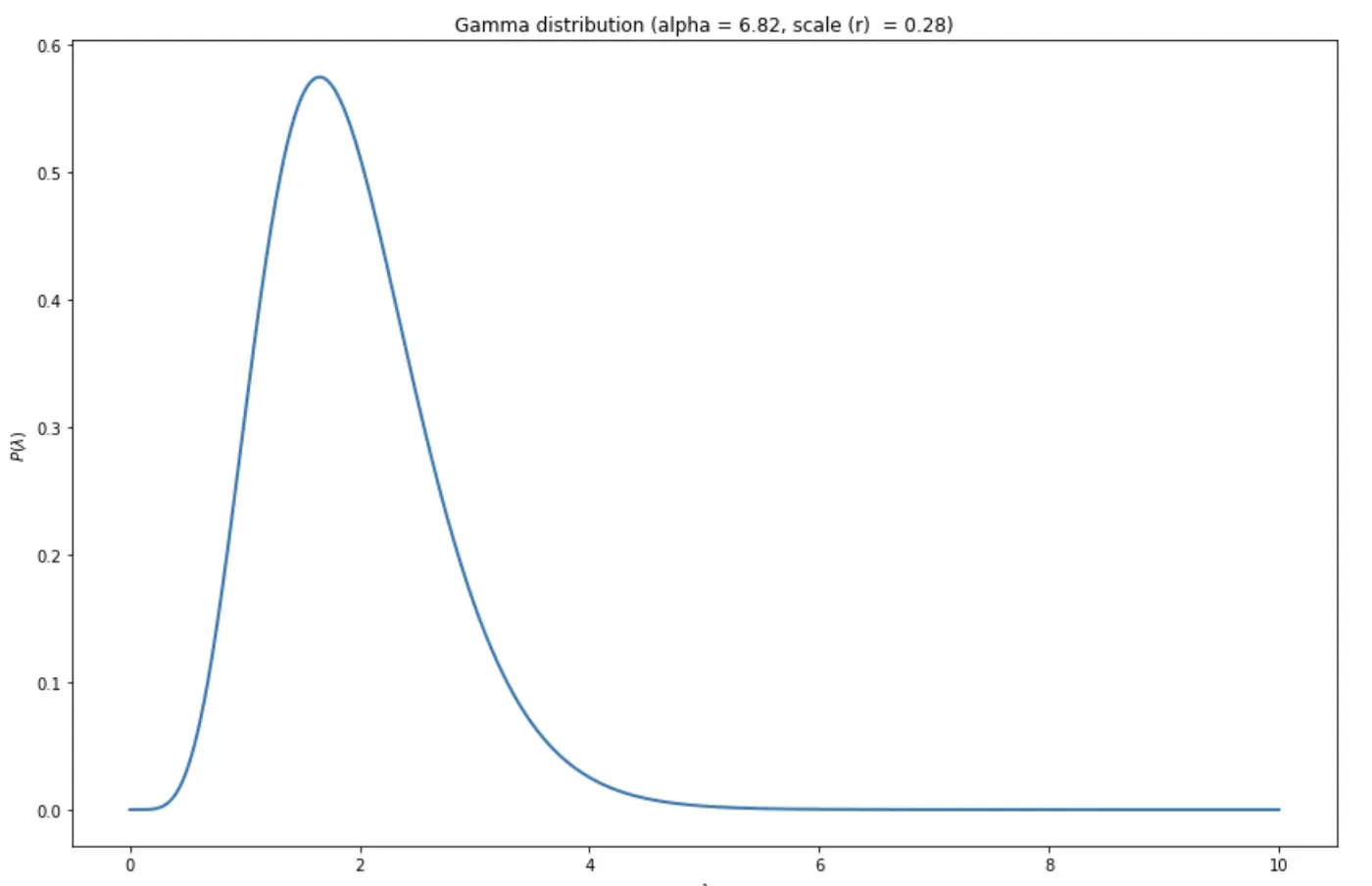
正如我们在第 1 部分中所讨论的,Gamma 分布具有实际意义——它定量地描述了我们客户群的集体购买行为。具体来说,它表明了人口中购买率的分布。上图显示了一个相对理想的 Gamma 分布,其中大部分 𝜆 都在 2 附近。这意味着我们的客户预计以每周 2 次交易的速度购物——对于 CD 公司来说,这不是一个糟糕的速度!
现在让我们看一下 Beta 分布,它描述了我们客户群中停用概率 p 的分布:
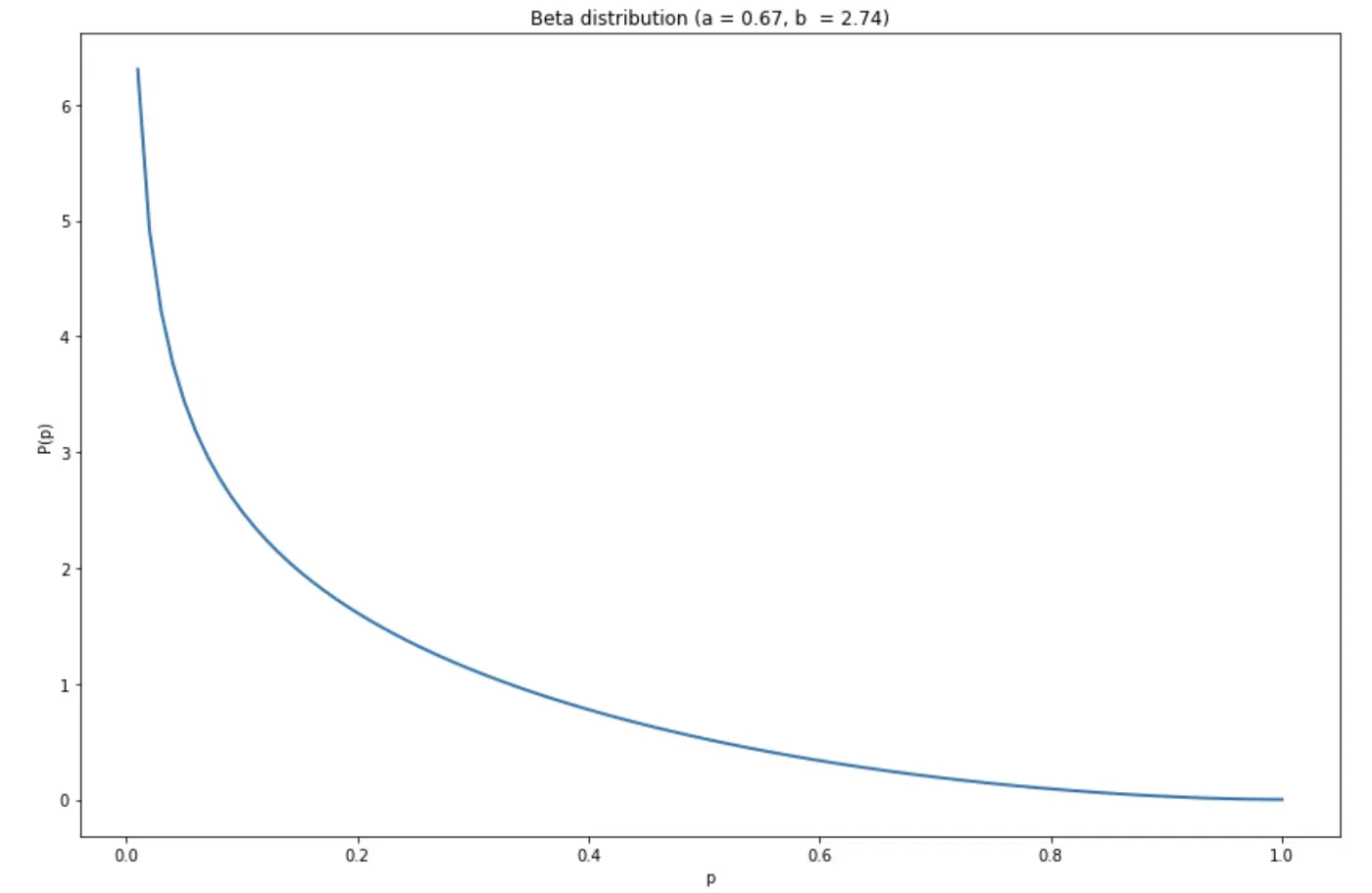
该图显示了一个相对健康的 Beta 分布,其大部分 p 集中在 0 附近。这意味着作为一个整体,我们的客户不太可能停用。
Conclusion
在本系列文章中,我们讨论了 BG-NBD 模型的基本原理,并展示了它在解决实际业务问题中的价值。
具体来说,在文章 1 中,我们了解到 BG-NBD 对客户群体的重复购买行为和停用概率进行建模。由此产生的概率分布不仅在理论上是合理的;它们还提供了我们个人客户和客户群的有见地的定量表示。
在文章 2 中,我们探讨了生命周期,即 BG-NBD 的常客实现。生命周期允许我们用几行代码拟合 BG-NBD 模型。我们还看到了几种使用生命周期输出的实用方法。对于不想手动编写 BG-NBD 方程并希望立即开始获取业务价值的分析师,我建议他们使用生命周期。
第三篇也是最后一篇文章使用贝叶斯 PyMC3 库实现了 BG-NBD。此实现涉及从头开始编码 BG-NBD,因此需要对模型有更深入的了解。优点是它允许我们指定先验,这允许我们将我们的专业知识融入建模过程。对于既熟悉 BG-NBD 又熟悉他们试图建模的客户群领域知识的从业者,我会推荐这种方法。
References
[1] “计算您的客户”的简单方法:Pareto/NBD 模型的替代方案(Bruce Hardie 等人,2005 年)[0]
[2] 如果您对 PyMC3 的深入了解感兴趣,请查看这本很棒的书 Probabilistic Programming & Bayesian Methods for Hackers。[0]
[3] Stata 博客:贝叶斯统计简介(第 2 部分)—MCMC 和 Metroplis Hastings 算法[0]
[4] 轨迹绘图只是确认收敛的众多方法之一。 PyMC3 文档提供了对该主题的广泛处理。[0]
注意:除非另有说明,否则所有图像、图表、表格和方程式均由我创建。
如果您对本文有任何问题/意见或想与我联系,请随时通过 LinkedIn 或通过电子邮件发送至 meraldo.antonio AT gmail DOT com。[0]
文章出处登录后可见!
