如何处理优化问题

带有解决方案和代码的简单示例

变量、约束和目标

为了定义优化问题，您需要三件事：变量、约束和目标。变量可以取不同的值，求解器将尝试为变量找到最佳值。约束是不允许的事情或界限，通过正确设置这些，您可以确定您会找到一个可以在现实生活中实际使用的解决方案。目标是您在优化问题中的目标，这是您想要最大化或最小化的目标。如果现在还不完全清楚，这里有一个更彻底的介绍。不要犹豫继续，因为这些示例将指导您并更详细地解释这些概念。[0]

Code Examples

想象一下，您是一家小型包裹递送公司的 CEO。该公司发现交付流程可以改进。他们希望首先交付最有价值的包裹组合，并确定每次旅行的最短路线。他们最不想改进的就是任务分工。一些员工抱怨，因为他们希望更频繁地交付而不是对包裹进行分类。

如果您想自己尝试这些示例，您需要一个安装了以下软件包的工作 python 环境：pyomo、pandas 和 numpy。您还应该下载像 cbc 或 glpk 这样的求解器并在可执行路径中使用它。一些关于列表推导和 Python 编程的知识会很有帮助，本文不涉及。[0][1][2][3][4][5][6]

示例 1：选择要交付的包裹

一个包裹的价值越高，这个包裹对客户的重要性就越大。快递公司有一张表格，上面有包裹及其价值和重量：

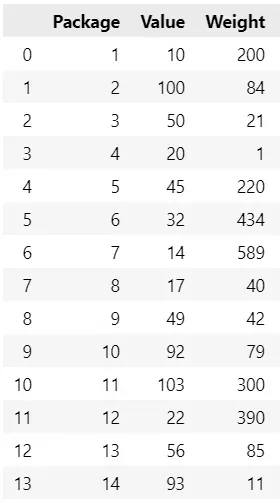
该公司希望选择总价值最高且总重量小于 600 的包裹（这是送货车可以处理的最高数量）。应该选择哪些包？目标很明确：我们希望最大化所选包的总价值。约束是所选包裹的总重量应小于或等于 600。我们可以将变量定义为每个包裹的二进制变量，如果未选择包裹，则该变量为零，如果包裹被选中，则该变量为零。选择。

让我们开始编程吧。

首先我们导入包，加载表并从表中提取数据（这使得下一部分的代码更具可读性）：

import numpy as np
import pandas as pd
import pyomo.environ as pyo
from pyomo.opt import SolverFactory
import time# load dataframe with package details
data = pd.read_excel('package_details.xlsx')# extracting the indici, weights and values from the dataframe
indici = list(data.index.values)
weights = data['Weight'].values
values = data['Value'].values

现在我们可以开始使用pyomo了：

# create a concrete model
model = pyo.ConcreteModel()# define the VARIABLES (in the end 0=not selected, 1=selected)
model.x = pyo.Var(indici, within=pyo.Binary)
x = model.x# define the CONSTRAINT, the total weight should be less than 600
model.weight_constraint = pyo.Constraint(expr= sum([x[p]*weights[p] for p in indici]) <= 600)# define the OBJECTIVE, we want to maximize the value of the selected packages
model.objective = pyo.Objective(expr= sum([x[p]*values[p] for p in indici]), sense=pyo.maximize)# print the complete model
model.pprint()

回想一下，该变量是一个二元决策变量，将等于 0（未选择）或 1（已选择）。该约束确保所选包裹的总重量为 600 或更少。为此，我们应该将 x 变量乘以包的权重并将这些值相加。目标计算所选包的值的总和（将 x 和包的值相乘并求和），我们想要最大化这个目标（sense=pyo.maximize）。 model.pprint() 显示定义的模型：

就这样！现在是时候调用求解器了，它会为我们提供我们应该选择的包：

# replace the executable path by your own
opt = SolverFactory('cbc', executable='C:\cbc\\bin\cbc.exe')
results = opt.solve(model)

在几秒钟内，求解器就找到了最优解！我们可以在原始数据框中添加一个解决方案列。

solution = [int(pyo.value(model.x[p])) for p in indici]
data['solution'] = solution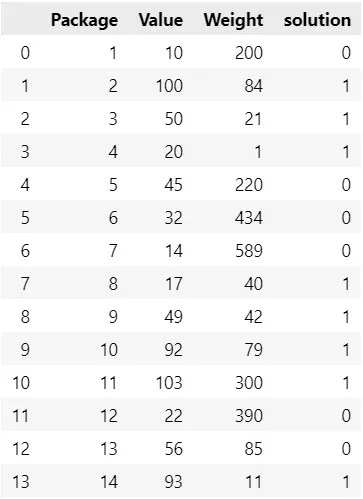

你能改变这个问题来选择最大数量的包裹而不是选择包裹的最高总值吗？

问题解决了，我们继续下一个！

示例 2：确定交付所选包裹的订单

为了尽快交付选定的包裹，我们希望采取最短的路线。我们从取件点开始，我们想在那里结束取件新包裹。我们如何建模这个问题并使用优化来解决它？这道题比上一道题要难一些。让我们定义目标、约束和变量。

目标是最小化路线的总距离。约束是：我们应该从取货点开始，在取货点结束，每个包裹都应该送达，所以我们需要至少访问所有地址一次。我们还需要确保创建一条完整的路线而不是多条小路线。最后但并非最不重要的，变量。我们使用二进制变量创建一个从到矩阵，其中 1 表示选择了这种方式，而 0 表示未选择。如果 x[6, 2] == 1 我们从地址 6 转到地址 2。

对于这个问题，我们需要一个距离矩阵。检查下面的矩阵，从地址 6 到地址 2 的距离等于 16。地址 0 是我们的起点（和终点）。我们需要递送 8 个包裹，由另外 8 个地址表示。

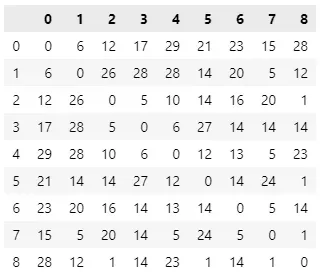
创建随机距离矩阵的代码：

import random
import pandas as pdindici = range(9)
distances = pd.DataFrame(index=indici, columns=indici)for from_ in indici:
   for to in indici:
      if from_ == to:
         distances.loc[from_, to] = 0
      elif pd.isna(distances.loc[from_, to]):
         dist = random.choice(range(1, 30))
         distances.loc[from_, to] = dist
         distances.loc[to, from_] = dist

首先我们声明模型、地址（距离矩阵的索引值列表）和变量：

model = pyo.ConcreteModel()addresses = distances.index# declaring the VARIABLE matrix, again with only binary values
model.x = pyo.Var(addresses, addresses, within=pyo.Binary)
x = model.x

在这个例子中，变量是一个矩阵：我们通过循环两次地址来创建它。所以 x[2,3] 对应地址 2 到地址 3 的路由。

现在是时候声明约束了。这次我们将使用约束列表，因为我们要同时添加多个约束。

第一个约束列表将保存我们往返于同一地址的值。我们不想激活它们，所以我们将所有变量值设置为 from 和 to 点相同等于零：

model.diagonal = pyo.ConstraintList()
for a in addresses:
   model.diagonal.add(expr= x[a, a] == 0)

下一个限制是关于访问每个地址一次。这意味着每个地址都应该是一次“收件人”地址，以及一次“发件人”地址。

model.visit_once = pyo.ConstraintList()
for a in addresses:
   model.visit_once.add(expr=sum([x[a, to] for to in addresses])==1)
   model.visit_once.add(expr=sum([x[fr, a] for fr in addresses])==1)

最后一个限制：我们不想绕圈旅行，我们想要一条完整的路线！因此，如果我们从地址 0 到地址 5，我们不想从地址 5 到地址 0！不应激活这两条路线或其中之一，因此 x[0, 5] + x[5, 0] <= 1 。此约束确保我们获得一条完整的路线，而不是多条较小的路线。查看 Miller-Tucker-Zemlin 公式以了解对该约束的解释。我们在这里引入一个名为 u 的虚拟变量。[0]

model.u = pyo.Var(addresses, within=pyo.NonNegativeIntegers, bounds=(1, n))
u = model.u
n = len(addresses)model.no_circles = pyo.ConstraintList()
for a1 in range(1, n):
   for a2 in range(1, n):
      if a1 != a2:
         model.no_circles.add(expr= u[a1]-u[a2]+x[a1,a2]*n <= n-1)

约束，检查！对于目标，我们希望最小化激活路线的距离总和。我们遍历地址组合并将 x 的值乘以路线的距离。这些值的总和为我们提供了总距离。这一次我们需要调用pyo.minimize，因为我们想要最小化总距离。

# declaring the OBJECTIVEsum_of_distances = sum([x[a1, a2]*distances.loc[a1, a2] for a1 in addresses for a2 in addresses])model.obj = pyo.Objective(expr=sum_of_distances, sense=pyo.minimize)

现在是解决问题的时候了。调用求解器并打印结果：

opt = SolverFactory('cbc', executable='C:\cbc\\bin\cbc.exe')
results = opt.solve(model)print(pyo.value(model.obj)) # gives 62 (for this distance matrix)solution = []
for a1 in addresses:
   solution.append([pyo.value(model.x[a1, a2]) for a2 in addresses])

目标的值为 62，因此这条路线的总距离等于 62。在您的情况下，它可能是另一个数字，因为您可能有另一个距离矩阵。解决方案矩阵如下所示：

每行有一个 1，每列也有一个 1。所以我们访问每个地址一次。要使此解决方案更具可读性，请使用以下代码：

def print_route(solution):
   sol_ind = list(np.where(np.array(solution[i]) == 1)[0][0] for i in range(len(solution)))
   one_dict = {k:sol_ind[k] for k, _ in enumerate(sol_ind)}   sol_str = '0 -> '
   nxt = one_dict[0]
   sol_str += str(nxt)
   while True: 
      nxt = one_dict[nxt]
      sol_str += ' -> '
      sol_str += str(nxt)
      if nxt == 0:
         break   print(sol_str)print_route(solution)

Result:

所以从起点（上车点，地址 0）我们去地址 2、地址 8、地址 5、地址 4，依此类推，直到我们回到上车点。我们交付了所有包裹，我们可以确定这是可用的最短路线之一！

注意：这个问题是旅行商问题的变体。[0]

你已经解决了两个问题，很好！让我们继续最后一个！

示例 3：任务分工

最后一个问题是关于任务划分的。目前，您有六名员工，您希望让他们保持快乐和充满活力。但与此同时，工作需要完成！那么，您如何才能既完成工作又让员工开心呢？很简单，您创建另一个优化模型！您定义需要完成的任务，例如清洁、分类包裹、递送包裹和在服务中心。在接下来的一个月中，您可以定义每项任务需要多少班次，以及每次班次需要多长时间。这为您提供了需要员工工作的总时间，并且您希望为每位员工提供相同的工作时间，以执行他们喜欢的任务。

# no of shifts needed for the upcoming month
DELIVERIES = 45
SORTING = 20
SERVICE_CENTER = 20
CLEANING = 10task = {'DELIVERY': DELIVERIES, 'SORT': SORTING, 'SERVICE': SERVICE_CENTER, 'CLEAN': CLEANING}# time needed for every shift
time_p_shift = {'DELIVERY': 8, 'SORT': 4, 'SERVICE': 6, 'CLEAN': 3}# total time needed 
total_hours = sum([task[k]*timepershift[k] for k in task.keys()])

接下来，你定义你的员工，让他们决定他们喜欢做什么轮班。

employees = {'John':['DELIVERY', 'CLEAN'], 'Jack':['DELIVERY'], 'Joshua':['SORT', 'CLEAN'], 'Janice':['DELIVERY', 'SERVICE'], 'Joyce':['DELIVERY', 'CLEAN', 'SERVICE', 'SORT'], 'Joy':['CLEAN', 'SERVICE', 'SORT']}emp_list = employees.keys()

John 喜欢送货和打扫，而 Joy 喜欢打扫、待在服务台和分拣包裹（她可能没有驾照）。现在您可以计算每个人应该工作的平均小时数，您将在目标中使用此值：

avg_hours_pp = total_hours/len(emp_list)final_df = pd.DataFrame(index=emp_list, columns=task.keys())

final_df 最终会收到最优值：

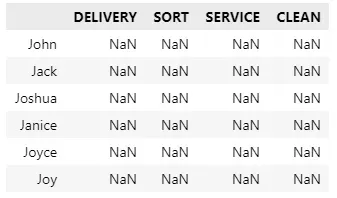
如果 x[‘John’, ‘DELIVERY’] == 6 John 这个月应该有六次送货班次。

数据处理完毕后，我们就可以开始建模了。我们使用员工和任务创建一个变量矩阵。

model = pyo.ConcreteModel()model.Employees = pyo.Set(initialize=emp_list)
model.Tasks = pyo.Set(initialize=task.keys())# define the VARIABLE matrix x using the employees and the tasks
model.x = pyo.Var(model.Employees, model.Tasks, within=pyo.Integers, bounds=(0, None))# define the hours of work per task
model.hours = pyo.Param(model.Tasks, initialize=time_p_shift)

我们希望每个班次都被填补，因此我们需要添加约束以确保我们有足够的人员来完成每项任务：

model.shifts_needed = pyo.ConstraintList()
for t in model.Tasks:
   model.shifts_needed.add(expr= sum([model.x[employee, t] for employee in model.Employees]) == task[t])

我们想排除人们不想做的某些任务：

model.excluded = pyo.ConstraintList()
for employee in model.Employees:
   incl = employees[employee]
   excl_tasks = list(task.keys()-incl)
   for t in excl_tasks:
      model.excluded.add(expr= model.x[employee, t] == 0)

我们的目标是为所有员工提供同等数量的工作，并且只提供他们想做的任务。我们怎样才能做到这一点？我们之前计算了平均小时数 avg_hours_pp。我们希望最小化从人们收到的小时数到 avg_hours_pp 的绝对距离。因为如果该距离等于 0，那么每个人都得到完全相同的工作量。

计算绝对距离是可能的，但不像使用 abs() 那样简单。 Pyomo 无法处理绝对函数，因为问题已经变得非线性。所以我们在这里引入两个新变量：model.posdelta 表示与 avg_hours_pp 的正距离，model.negdelta 表示负距离。使用约束列表，我们设置这些变量值：

model.posdelta = pyo.Var(model.Employees, bounds=(0, None))
model.negdelta = pyo.Var(model.Employees, bounds=(0, None))# defining the variables posdelta en negdelta using CONSTRAINTLIST
model.distance_from_avg = pyo.ConstraintList()
for employee in model.Employees:
   model.distance_from_avg.add(expr= sum([model.x[employee, t]*model.hours[t] for t in model.Tasks]) + model.posdelta[employee] - model.negdelta[employee] == avg_hours_pp)# defining the OBJECTIVE, minimize posdelta + negdelta
model.obj = pyo.Objective(expr= pyo.summation(model.posdelta) + pyo.summation(model.negdelta), sense=pyo.minimize)

是时候调用求解器并显示结果了：

opt = SolverFactory('cbc', executable='C:\cbc\\bin\cbc.exe')
results = opt.solve(model)def create_result_frame(model, df):
   solution = pd.DataFrame(np.reshape(pyo.value(model.x[:, :]), (df.shape[0], df.shape[1])), index=emp_list, columns=task.keys())
   solution = solution.astype('int')
   return solutionsolution = create_result_frame(model, final_df)

解决方案 DataFrame 如下所示：

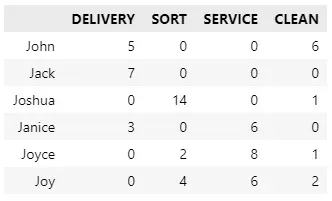
它向我们展示了每个人应该执行多少轮班。还有最重要的问题：任务是否平均分配？

for emp in model.Employees:
   print(f'{emp}:', int(sum([pyo.value(model.x[emp, t])*pyo.value(model.hours[t]) for t in model.Tasks])), 'hours')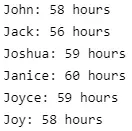

是的，每个人的工作量都差不多！

如果您想了解有关处理绝对值、线性化和其他高级概念的更多信息，请查看此处。[0]

Conclusion

我们在这篇文章中处理的问题是整数线性规划的例子。它是一种用于许多不同行业的技术，具有强大的功能。如果您的问题变得更大，像 CBC 这样的开源求解器将需要很长时间才能运行。您可能想要切换到 Gurobi 或 CPLEX 等商业求解器。如果你想将你的优化技能提升到一个新的水平，我可以推荐这个 Udemy 课程。[0][1][2][3]

如果您想在我发布新文章时收到电子邮件，请不要忘记订阅。[0]