1感知机

1.1单层感知机

1.1.1单层感知机的模型

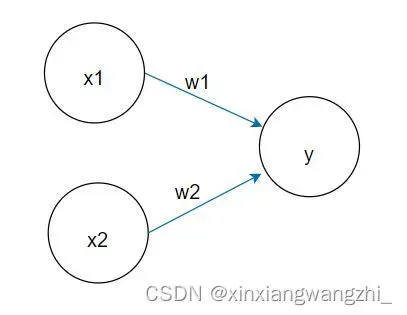
上图是一个接收两个输入信号的感知机的例子。是两个输入信号，是输出信号，是权重。图中的称为神经元或者节点。输入信号被送往神经元时，会分别乘以固定的权重，神经元会计算传送过来的信号总和。只有这个总共超过某一界限,才输出1。

1.1.2单层感知机的数学解释

上图用数学公式表示如下：

令,则（1）式变为：

式中：分别称为权重和偏差。权重控制输入参数的重要性，而偏差决定了神经元被激活的难易程度。
以上就是单层感知器的模型和数学解释。

1.1.3单层感知机的作用和局限性

使用单层感知器在电路中实现与门：
与门定义：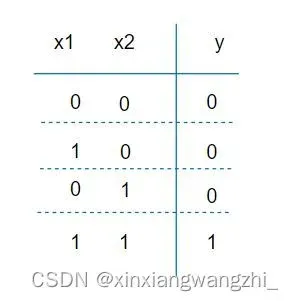

当且仅当都为真（1）时，.对于式（2）可以满足与门，同样也可以满足与门。可以发现：设置不同的权重和偏置可以实现与门，且参数方式不唯一。
同样，我们也可以通过设置权重和偏差来实现与非门和或门。
limitation:
无法通过设置权重和偏置利用单层感知机实现异或门（当且仅当、中仅有一个为1时y等于1）。

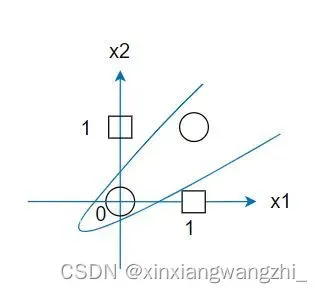
图中表示异或门，没有线性可分空间来表示异或门，单层感知机的局限就在于此。即：单层感知器只能表示线性空间，不能表示非线性空间。

1.2多层感知机

那么如何实现异或门呢？答案是多层感知器。
记NAND为与非门，AND与门，OR为或门，则异或门可以表示为：

非线性空间的异或门可以通过将单层感知器堆叠成多层感知器来实现。

多层感知器示意图
通过多层感知机，可以表示更加复杂的非线性空间。从与门、或门、与非门的线性组合可以表示更复杂的非线性电路，试着推广一下，线性组合可以表示任意复杂的电路。同样的，2层感知机（可以增加变量的个数即增加输入层神经元的个数）即可在理论上近似任何函数。