例题：
1. 某科学基金会的管理人员希望估计从事数学研究工作的中等或较高水平的数学家的年工资额Y与他们的研究成果（论文、著作等）的质量指标X1，从事研究工作的时间X2以及能成功获得资助的指标X3之间的关系。为此按一定的试验设计方法调查了24位此类型的数学家，得到下列数据：
| i | Xi1 | Xi2 | Xi3 | Yi |
| 1 | 3.5 | 9 | 6.1 | 33.2 |
| 2 | 5.3 | 20 | 6.4 | 40.3 |
| 3 | 5.1 | 18 | 7.4 | 38.7 |
| 4 | 5.8 | 33 | 6.7 | 46.8 |
| 5 | 4.2 | 31 | 7.5 | 41.4 |
| 6 | 6 | 13 | 5.9 | 37.5 |
| 7 | 6.8 | 25 | 6 | 39 |
| 8 | 5.5 | 30 | 4 | 40.7 |
| 9 | 3.1 | 5 | 5.8 | 30.1 |
| 10 | 7.2 | 47 | 8.3 | 52.9 |
| 11 | 4.5 | 25 | 5 | 38.2 |
| 12 | 4.9 | 11 | 6.4 | 31.8 |
| 13 | 8 | 23 | 7.6 | 43.3 |
| 14 | 6.5 | 35 | 7 | 44.1 |
| 15 | 6.6 | 39 | 5 | 42.8 |
| 16 | 3.7 | 21 | 4.4 | 33.6 |
| 17 | 6.2 | 7 | 5.5 | 34.2 |
| 18 | 7 | 40 | 7 | 48 |
| 19 | 4 | 35 | 6 | 38 |
| 20 | 4.5 | 23 | 3.5 | 35.9 |
| 21 | 5.9 | 33 | 4.9 | 40.4 |
| 22 | 5.6 | 27 | 4.3 | 36.8 |
| 23 | 4.8 | 34 | 8 | 45.2 |
| 24 | 3.9 | 15 | 5 | 35.1 |
2. 某医院管理工作者希望了解病人对医院工作的满意程度Y和病人的年龄X1，病情的严重程度X2和忧虑程度X3之间的关系，他随机的选取了23位病人，得到下列数据：
| i | Xi1 | Xi2 | Xi3 | Yi |
| 1 | 50 | 51 | 2.3 | 48 |
| 2 | 36 | 46 | 2.3 | 57 |
| 3 | 40 | 48 | 2.2 | 66 |
| 4 | 41 | 44 | 1.8 | 70 |
| 5 | 28 | 43 | 1.8 | 89 |
| 6 | 49 | 54 | 2.9 | 36 |
| 7 | 42 | 50 | 2.2 | 46 |
| 8 | 45 | 48 | 2.4 | 54 |
| 9 | 52 | 62 | 2.9 | 26 |
| 10 | 29 | 50 | 2.1 | 77 |
| 11 | 29 | 48 | 2.4 | 89 |
| 12 | 43 | 53 | 2.4 | 67 |
| 13 | 38 | 55 | 2.2 | 47 |
| 14 | 34 | 51 | 2.3 | 51 |
| 15 | 53 | 54 | 2.2 | 57 |
| 16 | 36 | 49 | 2 | 66 |
| 17 | 33 | 56 | 2.5 | 79 |
| 18 | 29 | 46 | 1.9 | 88 |
| 19 | 33 | 49 | 2.1 | 60 |
| 20 | 55 | 51 | 2.4 | 49 |
| 21 | 29 | 52 | 2.3 | 77 |
| 22 | 44 | 58 | 2.9 | 52 |
| 23 | 43 | 50 | 2.3 | 60 |
实验代码：
1、代码1
proc import out=temp1
datafile="C:\Users\86166\Desktop\IT\SAS实验\实验5\1.xls"
DBMS=EXCEL2000 replace;
run;
Data temp2;
set temp1;
Xi4=Xi1*Xi2;
Xi5=Xi1*Xi3;
Xi6=Xi2*Xi3;
run;
/*得回归方程，残差向量，残差图，残差正太概率图，回归方程显著性判断，回归参数的置信区间*/
proc reg data=temp2;
var Xi1-Xi6;
model Yi=Xi1-Xi3/cli clb r ss2;
plot r.*p. r.*Xi1 r.*Xi2 r.*Xi3 r.*Xi4 r.*Xi5 r.*Xi6 npp.*r.;
run;
/*检验回归参数是否相等利用restrict*/
proc reg data=temp1;
model Yi=Xi1-Xi3/ss2;
restrict Xi1=Xi2;
run;
2、代码2
proc import out=temp1
datafile="C:\Users\86166\Desktop\IT\SAS实验\实验5\2.xls"
DBMS=EXCEL2000 replace;
run;
data t;
set temp1;
z=(Yi**0.07-1)/0.07;
run;
/*R-Squre,MSE,CP法选择最优方程*/
proc reg data=temp1;
model Yi=Xi1-Xi3/selection=rsquare mse cp;
run;
/*PRESS法选择最优方程*/
proc reg data=t;
model z=Xi1/noprint;
output out=temp2 press=press;
run;
proc means uss data=temp2;
var press;
run;
proc reg data=t;
model z=Xi2/noprint;
output out=temp3 press=press;
run;
proc means uss data=temp3;
var press;
run;
proc reg data=t;
model z=Xi3/noprint;
output out=temp4 press=press;
run;
proc means uss data=temp4;
var press;
run;
proc reg data=t;
model z=Xi1 Xi2/noprint;
output out=temp5 press=press;
run;
proc means uss data=temp5;
var press;
run;
proc reg data=t;
model z=Xi1 Xi3/noprint;
output out=temp6 press=press;
run;
proc means uss data=temp6;
var press;
run;
proc reg data=t;
model z=Xi2 Xi3/noprint;
output out=temp7 press=press;
run;
proc means uss data=temp7;
var press;
run;
proc reg data=t;
model z=Xi1-Xi3/noprint;
output out=temp8 press=press;
run;
proc means uss data=temp8;
var press;
run;
proc reg data=temp1;
model Yi=Xi1 Xi3;
run;
/*逐步回归法选择最优方程*/
proc reg data=temp1;
model Yi=Xi1-Xi3/selection=stepwise;
run;实验结果：
图片太多，已打包在这里请自行查看：——》实验结果图片和数据集
分析实验结果：
1.对代码1：
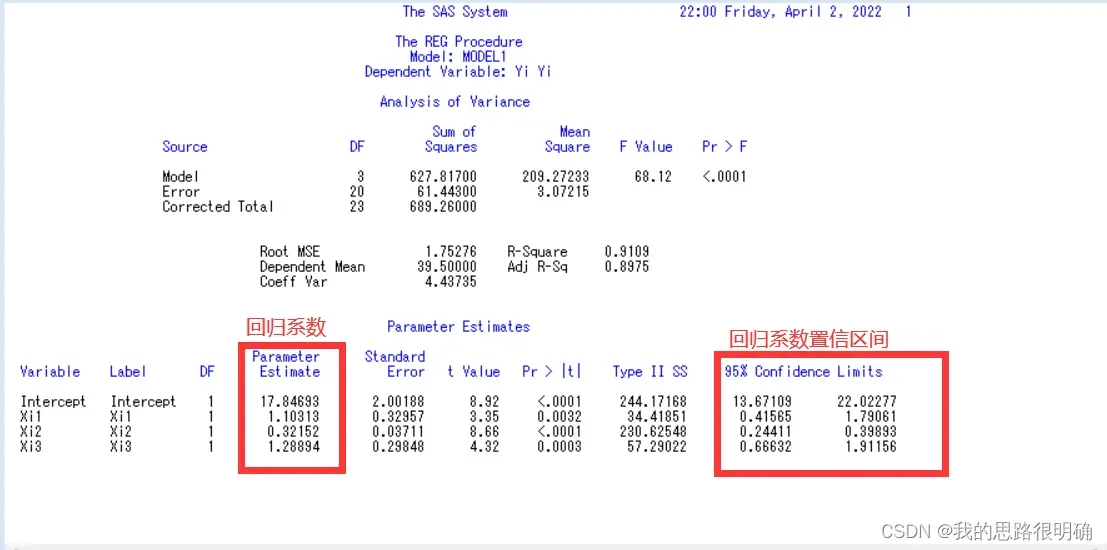
（1）统计关键词clb是求回归系数的置信度为95%的置信区间。
（2）根据F值68.12和P值<0.001<0.05，所以拒绝原假设，接受备择假设，认为Yi与Xi1-Xi3之间具有显著的线性相关关系，即回归方程是显著的；
（3）由R-Square的值为0.9109可知该方程的拟合度很高，样本观察值有91.09%的信息可以用回归方程进行解释，故拟合效果较好，认为Yi与Xi1-Xi3之间具有显著的线性相关关系。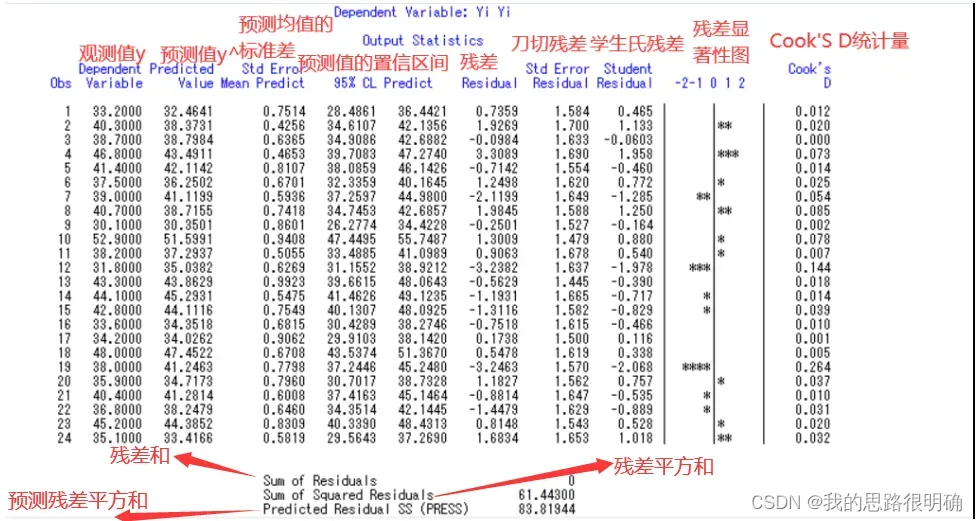
（4）统计关键词cli是求预测值的置信度为95%的置信区间，r是作残差分析，能得到刀切残差，学生氏残差，残差显著图，Cook’S D统计量。所以由图中可得残差向量为：
(
)’，也就是图中残差这一列。
（5）残差关于
，X1，X2，X3及两自变量交叉项的残差图及残差的正态概率图对应的是：plot r.*p. r.*Xi1 r.*Xi2 r.*Xi3 r.*Xi4 r.*Xi5 r.*Xi6 npp.*r.，由残差的正太概率图知，残差基本分布在一条直线上，所以基本可以认为残差服从正太分布。
（6）model Yi=Xi1-Xi3/ss2; restrict Xi1=Xi2;从图中看出当置信水平a=0.01时，P值<0.0001<0.01,说明回归分程具有显著的线性相关性，即满足了约束条件Xi1=Xi2下
，RESTRICT对应的SS2说明增加了这个约束条件损失了回归平方和15.60337，但换来了模型的简化，这个数值越小，说明这个约束条件越客观存在。（也可以用test Xi1=Xi2）
2.对代码2：
（1）在proc reg过程中指定selection=rsquare mse cp来进行对应准则下的变量筛选。
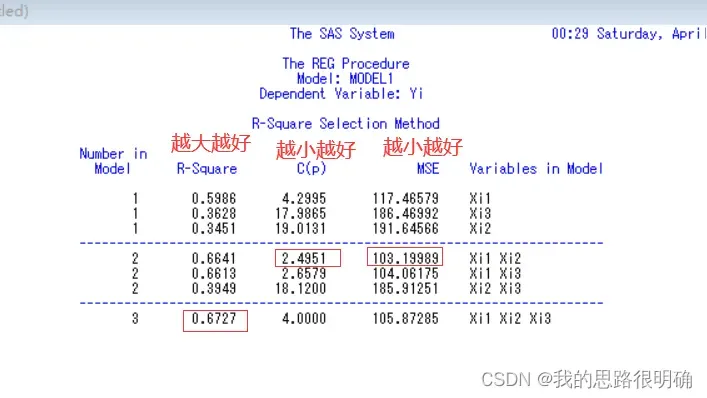从图中可知R²准则保留所有变量，Cp准则和MSE准则下只保留Xi1和Xi2。
PRESS(预测平方和准则)，可以向上述代码中这样写，也可以对所有变量的组合直接进行proc reg过程并带上统计关键词r，得到的第二张表里面有Predicted Residual SS(PRESS)，然后把每个值都进行比较，取值最小的那个。所以根据该准则，USS=1.5990749最小只保留Xi1和Xi3。
由此可见，四个准则下，最优回归方程并不一致。
（2）给定了F检验临界值，Fenter(变量进入)=3.0,Fdelete(变量删除)=2.9,满足了Fe>=Fd。
在这个条件下进行逐步回归过程，如果直接model Yi=Xi1-Xi3/selection=stepwise；那么默认SLE和SLS是0.15(也就是变量进入时偏F检验对应的显著水平a=0.15，和变量删除时偏F检验对应的显著水平a=0.15)，再在这个条件下得到最终保留下来的变量，这个时候删除的变量对应的F值是无法知道的。所以直接用题目给定的Fe和Fd来判断变量的保留和舍去是有一定局限的。这里有两种办法来解决：
①设置SLE和SLS为0.99，基本上就是保留所有变量了，然后利用Fe和Fd对逐步回归得到的变量的F值进行判断是舍还是留。
②Fe和Fd对应的显著水平a，因为这时候F值和自由度n-p-1都是知道的，所以根据F检验临界表可以得到对应的显著水平a，就可以在直接得到在指定的SLE和SLS下得到最终逐步回归的结果。
文章出处登录后可见！
