14.1 相关概念
1、 数学计算的网站:Wolfram|Alpha: Computational Intelligence
2、SymPy 是一个用于符号数学的 Python 库:SymPy
导数(Derivative)的精髓在于“变化率”
假设:
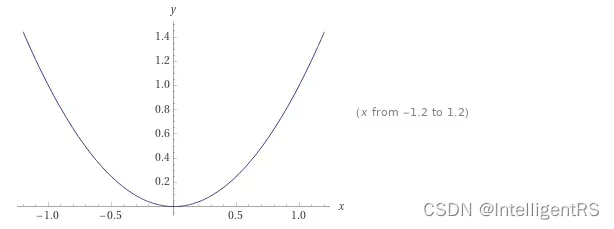
那么其导数为:
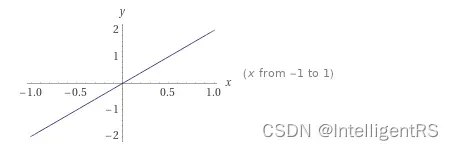
假设:
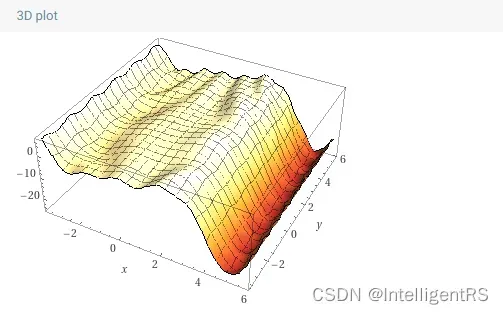
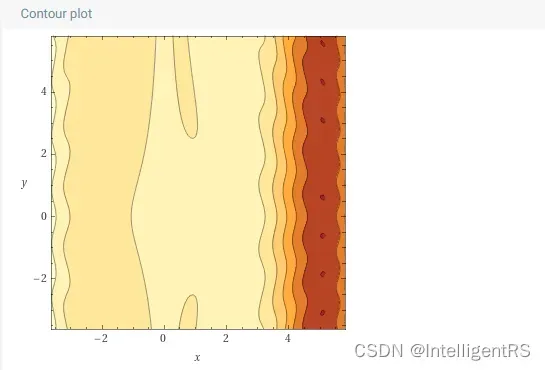
其偏导数为:
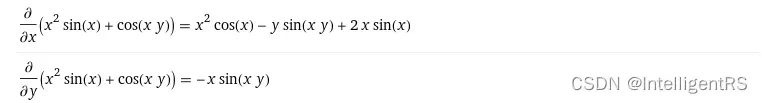
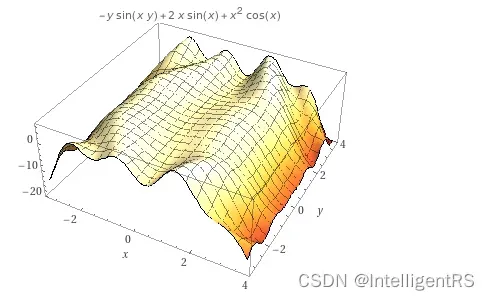
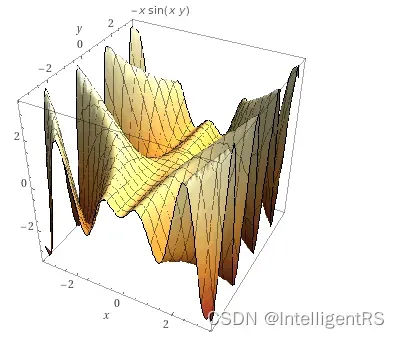
3D绘图
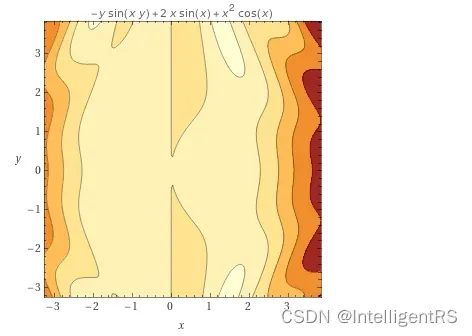
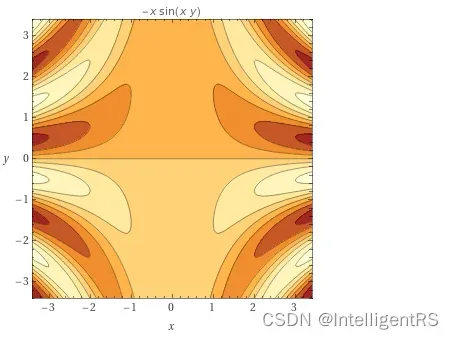
等高线图
14.2 通过Sympy库计算求导结果
# -*- coding: utf-8 -*-
"""
Created on Tue May 17 11:25:13 2022
@author: xiaofeng
"""
import sympy as sym
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
def func(x, y):
return x ** 2 * y + np.cos(y) + np.sin(x)
if __name__ == '__main__':
sym.init_printing()
x, y = sym.symbols("x y")
f = x ** 2 * y + sym.cos(y) + sym.sin(x)
# 只是显示数学公式,并不会得出求导结果(在notebook里就可以显示出标准的数学公式)
sym.Derivative(f, x)
# 可算出求导结果
print(sym.diff(f, x))
print(sym.diff(f, y))
# 创建等差数列
x = np.linspace(-888, 888, 8)
y = np.linspace(-888, 888, 8)
X, Y = np.meshgrid(x, y)
Z = func(X, Y)
fig = plt.figure(figsize=(15, 8))
ax = plt.axes(projection="3d")
ax.contour3D(X, Y, Z, 5, cmap="binary")
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap="viridis", edgecolor="none")
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")
plt.show()
运行结果为:
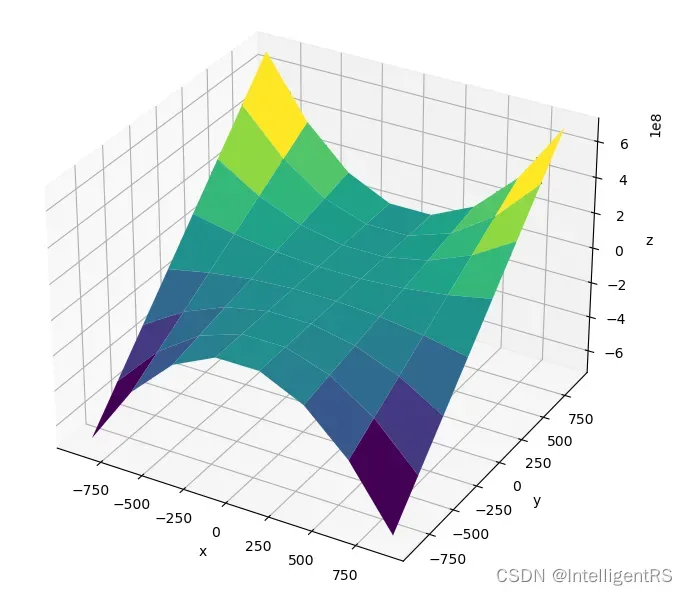
14.3 梯度(Gradient)
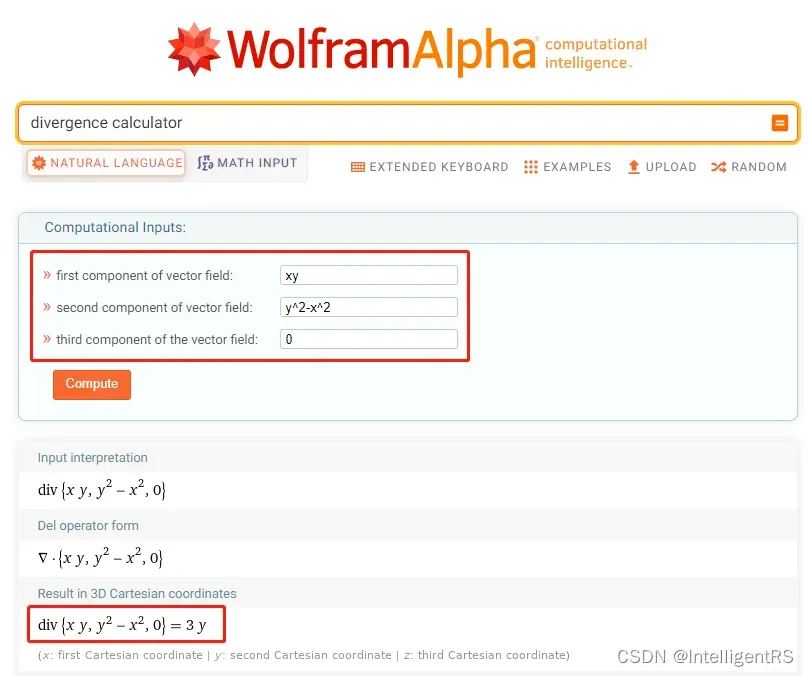
14.4 散度(Divergence)
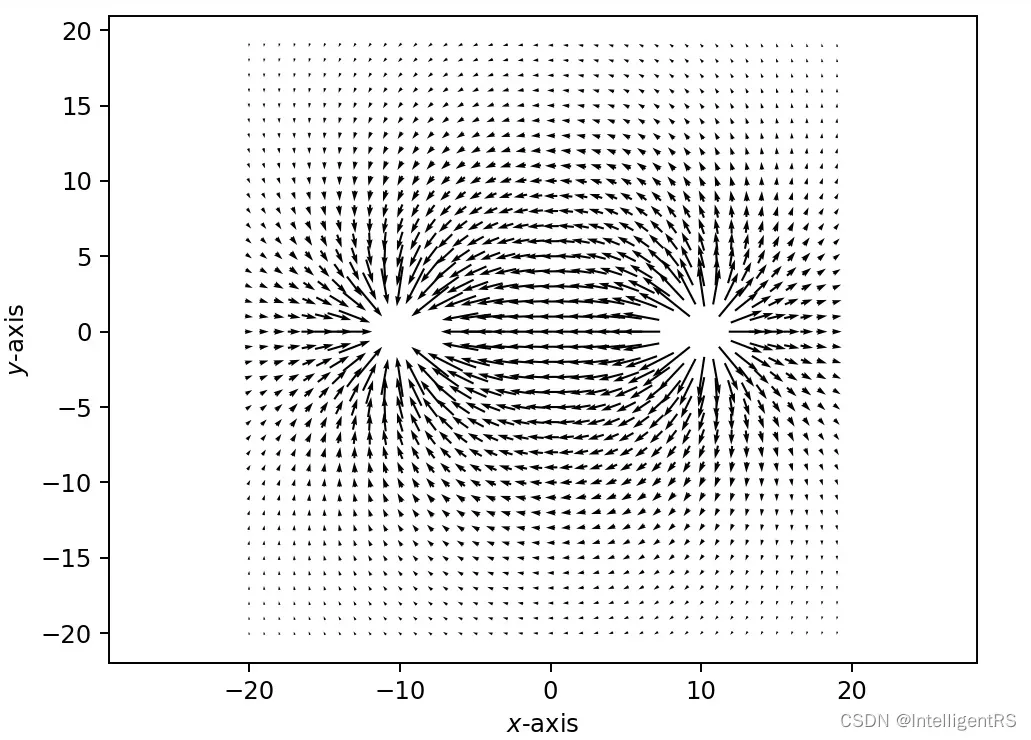
假设:
文章出处登录后可见!
已经登录?立即刷新
