线性回归

在机器学习领域中的⼤多数任务通常都与预测（prediction）有关。当我们想预测⼀个数值时，就会涉及到回归问题。常⻅的例⼦包括：预测价格（房屋、股票等）、预测住院时间（针对住院病⼈等）、预测需求（零售销量等）。但不是所有的预测都是回归问题。在后⾯的章节中，我们将介绍分类问题。分类问题的⽬标是预测数据属于⼀组类别中的哪⼀个。

线性回归基本元素

为了解释线性回归，我们举⼀个实际的例⼦：我们希望根据房屋的⾯积（平⽅英尺）和房龄（年）来估算房屋价格（美元）。为了开发⼀个能预测房价的模型，我们需要收集⼀个真实的数据集。这个数据集包括了房屋的销售价格、⾯积和房龄。在机器学习的术语中，该数据集称为训练数据集（training data set）或训练集（training set）。每⾏数据（⽐如⼀次房屋交易相对应的数据）称为样本（sample），也可以称为数据点（data point）或数据样本（data instance）。我们把试图预测的⽬标（⽐如预测房屋价格）称为标签（label）或⽬标（target）。预测所依据的⾃变量（⾯积和房龄）称为特征（feature）或协变量（covariate）。

由于平⽅误差函数中的⼆次⽅项，估计值yˆ(i)和观测值y(i)之间较⼤的差异将导致更⼤的损失。为了度量模型在整个数据集上的质量，我们需计算在训练集n个样本上的损失均值（也等价于求和）。

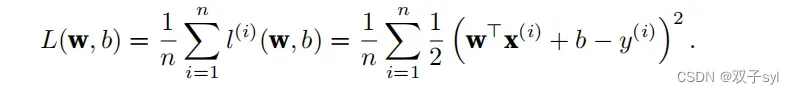
在训练模型时，我们希望寻找⼀组参数（w∗, b∗），这组参数能最⼩化在所有训练样本上的总损失。如下式：



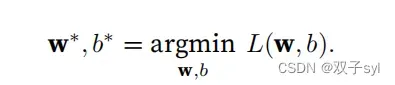
线性回归，前向传播的是计算得到的y‘值，然后根据y’-y计算loss，然后反向传播，每一个特征（相当于邻接矩阵的那些列）的loss分别对w和b求偏导，得到每一个特征的梯度，也就是3.1.10式子，以此来更新w和b。

⽮量化加速

在训练我们的模型时，我们经常希望能够同时处理整个⼩批量的样本。为了实现这⼀点，需要我们对计算进⾏⽮量化，从⽽利⽤线性代数库，⽽不是在Python中编写开销⾼昂的for循环。

%matplotlib inline
import math
import time
import numpy as np
import torch
from d2l import torch as d2l
	n = 10000
	a = torch.ones(n)
	b = torch.ones(n)

由于在本书中我们将频繁地进⾏运⾏时间的基准测试，所以我们定义⼀个计时器：

class Timer: #@save
"""记录多次运⾏时间"""
	def __init__(self):
		self.times = []
		self.start()
	def start(self):
"""启动计时器"""
	self.tik = time.time()
	def stop(self):
"""停⽌计时器并将时间记录在列表中"""
	self.times.append(time.time() - self.tik)
		return self.times[-1]
	def avg(self):
"""返回平均时间"""
		return sum(self.times) / len(self.times)
	def sum(self):
"""返回时间总和"""
		return sum(self.times)
	def cumsum(self):
"""返回累计时间"""
		return np.array(self.times).cumsum().tolist()

现在我们可以对⼯作负载进⾏基准测试。
⾸先，我们使⽤for循环，每次执⾏⼀位的加法。

	c = torch.zeros(n)
	timer = Timer()
	for i in range(n):
		c[i] = a[i] + b[i]
		f'{timer.stop():.5f} sec'
		'0.08976 sec'

或者，我们使⽤重载的+运算符来计算按元素的和。

timer.start()
d = a + b f'{timer.stop():.5f} sec'
'0.00027 sec'

正态分布和平方损失

接下来，我们通过对噪声分布的假设来解读平⽅损失⽬标函数。
正态分布和线性回归之间的关系很密切。正态分布（normal distribution），也称为⾼斯分布（Gaussian
distribution），最早由德国数学家⾼斯（Gauss）应⽤于天⽂学研究。简单的说，若随机变量x具有均值µ和⽅差σ2（标准差σ），其正态分布概率密度函数如下：

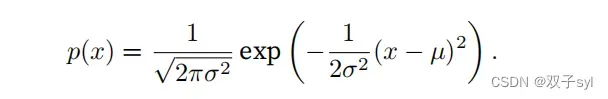
下⾯我们定义⼀个Python函数来计算正态分布。

def normal(x, mu, sigma):
		p = 1 / math.sqrt(2 * math.pi * sigma**2)
		return p * np.exp(-0.5 / sigma**2 * (x - mu)**2)

我们现在可视化正态分布。

# 再次使⽤numpy进⾏可视化
x = np.arange(-7, 7, 0.01) # 均值和标准差对
params = [(0, 1), (0, 2), (3, 1)]
d2l.plot(x, [normal(x, mu, sigma) for mu, sigma in params], xlabel='x',
ylabel='p(x)', figsize=(4.5, 2.5),
legend=[f'mean {mu}, std {sigma}' for mu, sigma in params])

线性回归的从零开始实现

⽣成数据集

为了简单起⻅，我们将根据带有噪声的线性模型构造⼀个⼈造数据集。我们的任务是使⽤这个有限样本的数据集来恢复这个模型的参数。我们将使⽤低维数据，这样可以很容易地将其可视化。在下⾯的代码中，我们⽣成⼀个包含1000个样本的数据集，每个样本包含从标准正态分布中采样的2个特征。我们的合成数据集是⼀个矩阵X ∈ R1000×2。我们使⽤线性模型参数w = [2, −3.4]⊤、b = 4.2 和噪声项ϵ⽣成数据集及其标签：
你可以将ϵ视为模型预测和标签时的潜在观测误差。在这⾥我们认为标准假设成⽴，即ϵ服从均值为0的正态分布。为了简化问题，我们将标准差设为0.01。下⾯的代码⽣成合成数据集。

%matplotlib inline
import random
import torch
from d2l import torch as d21
def synthetic_data(w, b, num_examples): #@save
    """生成 y = Xw + b + 噪声。"""
    X=torch.normal(0,1,(num_examples,len(w)))
    y=torch.matmul(X,w)+b#matmul所以矩阵向量乘法都可以通过广播机制实现
    y+=torch.normal(0,0.01,y.shape)
    return X,y.reshape(-1,1)
torch.normal(2,3,size=(1,4))
# tensor([[-1.3987, -1.9544,  3.6048,  0.7909]])
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features,labels=synthetic_data(true_w,true_b,1000)
features,labels
d2l.set_figsize()
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1);

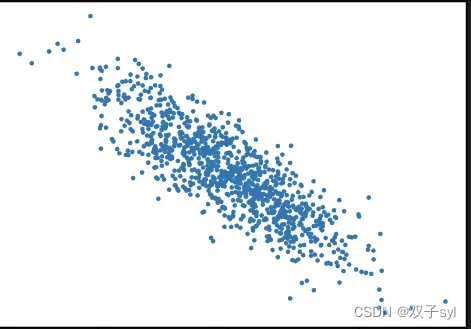
读取数据集

回想⼀下，训练模型时要对数据集进⾏遍历，每次抽取⼀⼩批量样本，并使⽤它们来更新我们的模型。由于这个过程是训练机器学习算法的基础，所以有必要定义⼀个函数，该函数能打乱数据集中的样本并以⼩批量⽅式获取数据。在下⾯的代码中，我们定义⼀个data_iter函数，该函数接收批量⼤⼩、特征矩阵和标签向量作为输⼊，⽣成⼤⼩为batch_size的⼩批量。每个⼩批量包含⼀组特征和标签。

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))#0-999的数组列表
    # 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices)#打乱顺序
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(
            indices[i: min(i + batch_size, num_examples)])#tensor([993, 616, 127, 509, 119, 167, 648, 486, 907,  27])前十个
        yield features[batch_indices], labels[batch_indices]
    #yield可以理解为一个return操作，但是和return又有很大的区别，执行完return，当前函数就终止了，函数内部的所有数据，所占的内存空间，全部都没有了。
    #而yield在返回数据的同时，还保存了当前的执行内容，当你再一次调用这个函数时，他会找到你在此函数中的yield关键字，然后从yield的下一句开始执行。

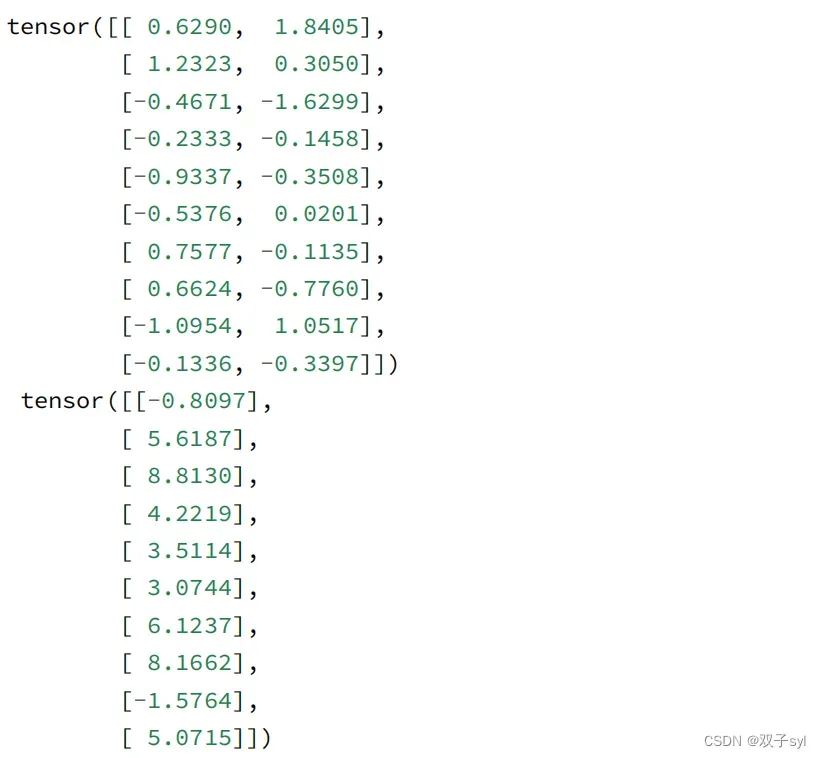
通常，我们利⽤GPU并⾏运算的优势，处理合理⼤⼩的“⼩批量”。每个样本都可以并⾏地进⾏模型计算，且每个样本损失函数的梯度也可以被并⾏计算。GPU可以在处理⼏百个样本时，所花费的时间不⽐处理⼀个样本时多太多。我们直观感受⼀下⼩批量运算：读取第⼀个⼩批量数据样本并打印。每个批量的特征维度显⽰批量⼤⼩和输⼊特征数。同样的，批量的标签形状与batch_size相等。

batch_size = 10
for X, y in data_iter(batch_size, features, labels):
	print(X, '\n', y)
	break

初始化模型参数

在我们开始⽤⼩批量随机梯度下降优化我们的模型参数之前，我们需要先有⼀些参数。在下⾯的代码中，我们通过从均值为0、标准差为0.01的正态分布中采样随机数来初始化权重，并将偏置初始化为0。

w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
 b = torch.zeros(1, requires_grad=True)

在初始化参数之后，我们的任务是更新这些参数，直到这些参数⾜够拟合我们的数据。每次更新都需要计算损失函数关于模型参数的梯度。有了这个梯度，我们就可以向减⼩损失的⽅向更新每个参数。因为⼿动计算梯度很枯燥⽽且容易出错，所以没有⼈会⼿动计算梯度。我们使⽤ 2.5节中引⼊的⾃动微分来计算梯度。
接下来，我们必须定义模型，将模型的输⼊和参数同模型的输出关联起来。回想⼀下，要计算线性模型的输出，我们只需计算输⼊特征X和模型权重w的矩阵-向量乘法后加上偏置b。注意，上⾯的Xw是⼀个向量，⽽b是⼀个标量。回想⼀下 2.1.3节中描述的⼴播机制：当我们⽤⼀个向量加⼀个标量时，标量会被加到向量的每个分量上。

def linreg(X, w, b): #@save
"""线性回归模型"""
	return torch.matmul(X, w) + b

因为需要计算损失函数的梯度，所以我们应该先定义损失函数。这⾥我们使⽤ 3.1节中描述的平⽅损失函数。在实现中，我们需要将真实值y的形状转换为和预测值y_hat的形状相同。

def squared_loss(y_hat, y): #@save
"""均⽅损失"""
	return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

正如我们在 3.1节中讨论的，线性回归有解析解。尽管线性回归有解析解，但本书中的其他模型却没有。这⾥我们介绍⼩批量随机梯度下降。在每⼀步中，使⽤从数据集中随机抽取的⼀个⼩批量，然后根据参数计算损失的梯度。接下来，朝着减少损失的⽅向更新我们的参数。下⾯的函数实现⼩批量随机梯度下降更新。该函数接受模型参数集合、学习速率和批量⼤⼩作为输⼊。每⼀步更新的⼤⼩由学习速率lr决定。因为我们计算的损失是⼀个批量样本的总和，所以我们⽤批量⼤⼩（batch_size）来规范化步⻓，这样步⻓⼤⼩就不会取决于我们对批量⼤⼩的选择。

def sgd(params, lr, batch_size): #@save
"""⼩批量随机梯度下降"""
	with torch.no_grad():
		for param in params:
			param -= lr * param.grad / batch_size
			param.grad.zero_()

训练

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  # `X`和`y`的小批量损失
        # 因为`l`形状是(`batch_size`, 1)，而不是一个标量。`l`中的所有元素被加到一起，
        # 并以此计算关于[`w`, `b`]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
epoch 1, loss 0.043118
epoch 2, loss 0.000173
epoch 3, loss 0.000051

print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')
w的估计误差: tensor([ 0.0005, -0.0004], grad_fn=<SubBackward0>) 
b的估计误差: tensor([0.0013], grad_fn=<RsubBackward1>)

线性回归简洁实现

生成数据集

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)

读取数据集

我们可以调⽤框架中现有的API来读取数据。我们将features和labels作为API的参数传递，并通过数据
迭代器指定batch_size。此外，布尔值is_train表⽰是否希望数据迭代器对象在每个迭代周期内打乱数
据。

def load_array(data_arrays, batch_size, is_train=True): #@save
"""构造⼀个PyTorch数据迭代器"""
	dataset = data.TensorDataset(*data_arrays)
	return data.DataLoader(dataset, batch_size, shuffle=is_train)
batch_size = 10
data_iter = load_array((features, labels), batch_size)

使⽤data_iter的⽅式与我们在 3.2节中使⽤data_iter函数的⽅式相同。为了验证是否正常⼯作，让我们
读取并打印第⼀个⼩批量样本。与 3.2节不同，这⾥我们使⽤iter构造Python迭代器，并使⽤next从迭代器中获取第⼀项。

next(iter(data_iter))

定义模型

对于标准深度学习模型，我们可以使⽤框架的预定义好的层。这使我们只需关注使⽤哪些层来构造模型，⽽不必关注层的实现细节。我们⾸先定义⼀个模型变量net，它是⼀个Sequential类的实例。Sequential类将多个层串联在⼀起。当给定输⼊数据时，Sequential实例将数据传⼊到第⼀层，然后将第⼀层的输出作为第⼆层的输⼊，以此类推。在下⾯的例⼦中，我们的模型只包含⼀个层，因此实际上不需要Sequential。但是由于以后⼏乎所有的模型都是多层的，在这⾥使⽤Sequential会让你熟悉“标准的流⽔线”。回顾 图3.1.2中的单层⽹络架构，这⼀单层被称为全连接层（fully-connected layer），因为它的每⼀个输⼊都通过矩阵-向量乘法得到它的每个输出。在PyTorch中，全连接层在Linear类中定义。值得注意的是，我们将两个参数传递到nn.Linear中。第⼀个指定输⼊特征形状，即2，第⼆个指定输出特征形状，输出特征形状为单个标量，因此为1。

# nn是神经⽹络的缩写
from torch import nn
net = nn.Sequential(nn.Linear(2, 1))

在使⽤net之前，我们需要初始化模型参数。如在线性回归模型中的权重和偏置。深度学习框架通常有预定义的⽅法来初始化参数。在这⾥，我们指定每个权重参数应该从均值为0、标准差为0.01的正态分布中随机采样，偏置参数将初始化为零。正如我们在构造nn.Linear时指定输⼊和输出尺⼨⼀样，现在我们能直接访问参数以设定它们的初始值。我们通过net[0]选择⽹络中的第⼀个图层，然后使⽤weight.data和bias.data⽅法访问参数。我们还可以使⽤替换⽅法normal_和fill_来重写参数值。

net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)

计算均⽅误差使⽤的是MSELoss类，也称为平⽅L2范数。默认情况下，它返回所有样本损失的平均值。

loss = nn.MSELoss()

⼩批量随机梯度下降算法是⼀种优化神经⽹络的标准⼯具，PyTorch在optim模块中实现了该算法的许多变种。当我们实例化⼀个SGD实例时，我们要指定优化的参数（可通过net.parameters()从我们的模型中获得）以及优化算法所需的超参数字典。⼩批量随机梯度下降只需要设置lr值，这⾥设置为0.03。

trainer = torch.optim.SGD(net.parameters(), lr=0.03)

训练

通过深度学习框架的⾼级API来实现我们的模型只需要相对较少的代码。我们不必单独分配参数、不必定义我们的损失函数，也不必⼿动实现⼩批量随机梯度下降。当我们需要更复杂的模型时，⾼级API的优势将⼤⼤增加。当我们有了所有的基本组件，训练过程代码与我们从零开始实现时所做的⾮常相似。
回顾⼀下：在每个迭代周期⾥，我们将完整遍历⼀次数据集（train_data），不停地从中获取⼀个⼩批量的输⼊和相应的标签。对于每⼀个⼩批量，我们会进⾏以下步骤:
• 通过调⽤net(X)⽣成预测并计算损失l（前向传播）。
• 通过进⾏反向传播来计算梯度。
• 通过调⽤优化器来更新模型参数。

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X) ,y)
        trainer.zero_grad()
        l.backward()
        trainer.step()
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')
epoch 1, loss 0.000392
epoch 2, loss 0.000104
epoch 3, loss 0.000104

下⾯我们⽐较⽣成数据集的真实参数和通过有限数据训练获得的模型参数。要访问参数，我们⾸先从net访问所需的层，然后读取该层的权重和偏置。正如在从零开始实现中⼀样，我们估计得到的参数与⽣成数据的真实参数⾮常接近。

w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)
w的估计误差： tensor([ 0.0002, -0.0002])
b的估计误差： tensor([-9.1553e-05])

softmax回归

分类问题

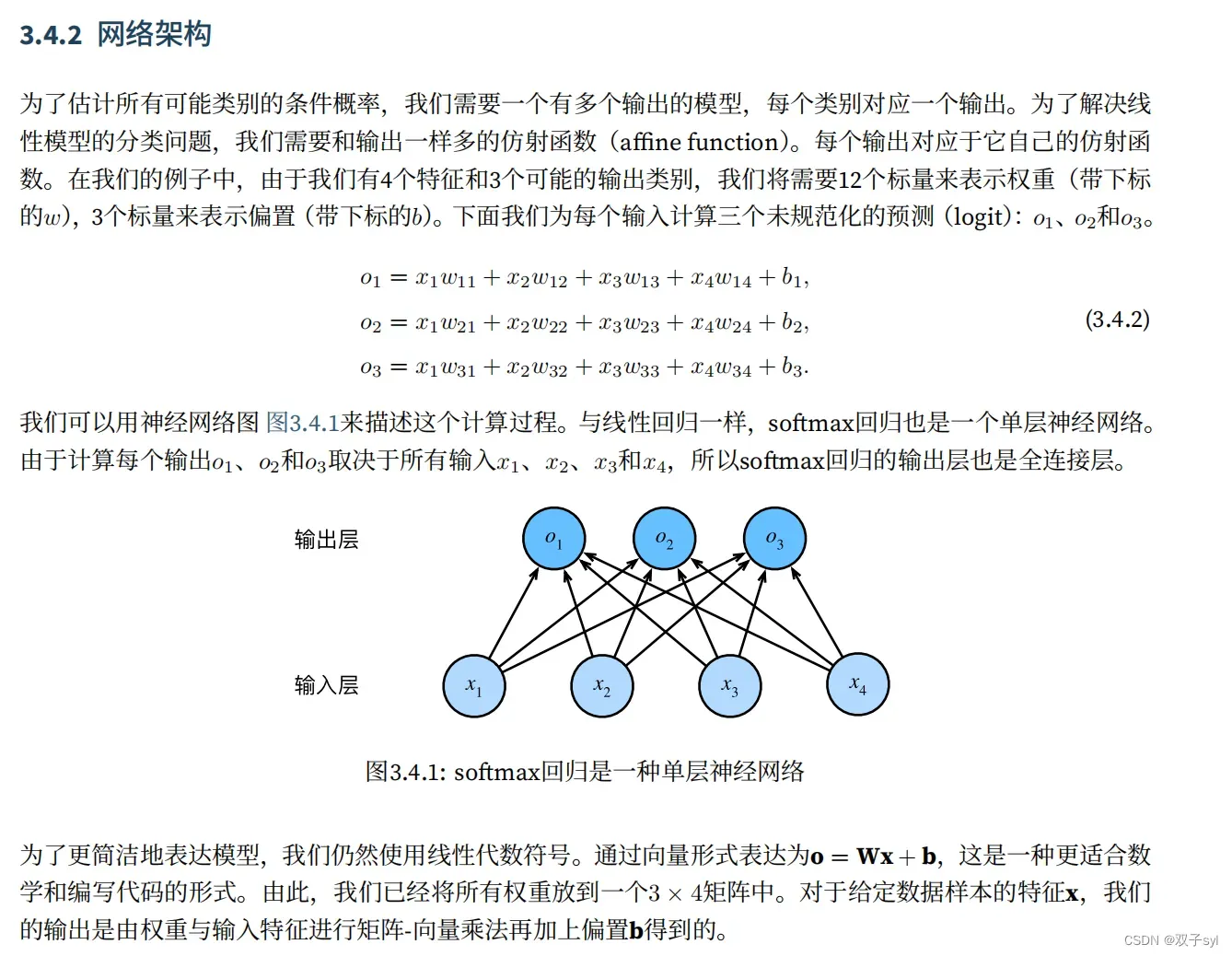
社会科学家邓肯·卢斯于1959年在选择模型（choice model）的理论基础上发明的softmax函数正是这样做的：softmax函数将未规范化的预测变换为⾮负并且总和为1，同时要求模型保持可导。我们⾸先对每个未规范化的预测求幂，这样可以确保输出⾮负。为了确保最终输出的总和为1，我们再对每个求幂后的结果除以它们的总和。如下式：

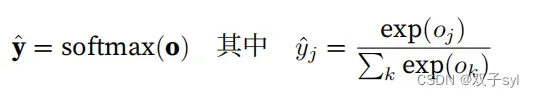
⼩批量样本的⽮量化

为了提⾼计算效率并且充分利⽤GPU，我们通常会针对⼩批量数据执⾏⽮量计算。假设我们读取了⼀个批量的样本X，其中特征维度（输⼊数量）为d，批量⼤⼩为n。此外，假设我们在输出中有q个类别。那么⼩批量特征为X ∈ Rn×d，权重为W ∈ Rd×q，偏置为b ∈ R1×q。softmax回归的⽮量计算表达式为：

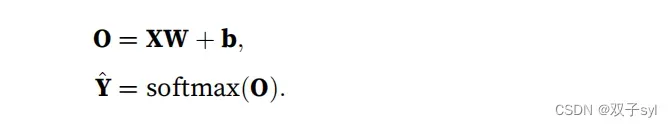
相对于⼀次处理⼀个样本，⼩批量样本的⽮量化加快了X矩阵-向量乘法。由于X中的每⼀⾏代表⼀个数
据样本，那么softmax运算可以按⾏（rowwise）执⾏：对于O的每⼀⾏，我们先对所有项进⾏幂运算，然后通过求和对它们进⾏标准化。在 (3.4.5)中，XW + b的求和会使⽤⼴播，⼩批量的未规范化预测O和输出概率ˆY都是形状为n × q的矩阵。

图像分类数据集

MNIST数据集 [LeCun et al., 1998] 是图像分类中⼴泛使⽤的数据集之⼀，但作为基准数据集过于简单。我们将使⽤类似但更复杂的Fashion-MNIST数据集 [Xiao et al., 2017]。

%matplotlib inline
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l
d2l.use_svg_display()

读取数据集

# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式，
# 并除以255使得所有像素的数值均在0到1之间
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(
    root="../data", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(
    root="../data", train=False, transform=trans, download=True)
    
len(mnist_train), len(mnist_test)
mnist_train[0][0].shape
torch.Size([1, 28, 28])

Fashion-MNIST由10个类别的图像组成，每个类别由训练数据集（train dataset）中的6000张图像和测试数据集（test dataset）中的1000张图像组成。因此，训练集和测试集分别包含60000和10000张图像。测试数据集不会⽤于训练，只⽤于评估模型性能。
每个输⼊图像的⾼度和宽度均为28像素。数据集由灰度图像组成，其通道数为1。为了简洁起⻅，本书将⾼度h像素、宽度w像素图像的形状记为h × w或（h,w）。
Fashion-MNIST中包含的10个类别，分别为t-shirt（T恤）、trouser（裤⼦）、pullover（套衫）、dress（连⾐裙）、coat（外套）、sandal（凉鞋）、shirt（衬衫）、sneaker（运动鞋）、bag（包）和ankle boot（短靴）。以下函数⽤于在数字标签索引及其⽂本名称之间进⾏转换。

def get_fashion_mnist_labels(labels):  #@save
    """返回Fashion-MNIST数据集的文本标签。"""
    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
                   'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    return [text_labels[int(i)] for i in labels]

我们现在可以创建⼀个函数来可视化这些样本

def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5):  #@save
    """绘制图像列表。"""
    figsize = (num_cols * scale, num_rows * scale)
    _, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize)
    axes = axes.flatten()
    for i, (ax, img) in enumerate(zip(axes, imgs)):
        if torch.is_tensor(img):
            # 图片张量
            ax.imshow(img.numpy())
        else:
            # PIL图片
            ax.imshow(img)
        ax.axes.get_xaxis().set_visible(False)
        ax.axes.get_yaxis().set_visible(False)
        if titles:
            ax.set_title(titles[i])
    return axes

以下是训练数据集中前⼏个样本的图像及其相应的标签。

X, y = next(iter(data.DataLoader(mnist_train, batch_size=18)))
show_images(X.reshape(18, 28, 28), 2, 9, titles=get_fashion_mnist_labels(y));

读取小批量

为了使我们在读取训练集和测试集时更容易，我们使⽤内置的数据迭代器，⽽不是从零开始创建。回顾⼀下，在每次迭代中，数据加载器每次都会读取⼀⼩批量数据，⼤⼩为batch_size。通过内置数据迭代器，我们可以随机打乱了所有样本，从⽽⽆偏⻅地读取⼩批量。

batch_size = 256

def get_dataloader_workers():  #@save
    """使用4个进程来读取数据。"""
    return 0

train_iter = data.DataLoader(mnist_train, batch_size, shuffle=True,
                             num_workers=get_dataloader_workers())
timer = d2l.Timer()
for X, y in train_iter:
    continue
f'{timer.stop():.2f} sec'

整合所有组件

现在我们定义load_data_fashion_mnist函数，⽤于获取和读取Fashion-MNIST数据集。这个函数返回
训练集和验证集的数据迭代器。此外，这个函数还接受⼀个可选参数resize，⽤来将图像⼤⼩调整为另⼀
种形状。

def load_data_fashion_mnist(batch_size, resize=None):  #@save
    """下载Fashion-MNIST数据集，然后将其加载到内存中。"""
    trans = [transforms.ToTensor()]
    if resize:
        trans.insert(0, transforms.Resize(resize))
    trans = transforms.Compose(trans)
    mnist_train = torchvision.datasets.FashionMNIST(
        root="../data", train=True, transform=trans, download=True)
    mnist_test = torchvision.datasets.FashionMNIST(
        root="../data", train=False, transform=trans, download=True)
    return (data.DataLoader(mnist_train, batch_size, shuffle=True,
                            num_workers=get_dataloader_workers()),
            data.DataLoader(mnist_test, batch_size, shuffle=False,
                            num_workers=get_dataloader_workers()))

下⾯，我们通过指定resize参数来测试load_data_fashion_mnist函数的图像⼤⼩调整功能。

	train_iter, test_iter = load_data_fashion_mnist(32, resize=64)
		for X, y in train_iter:
			print(X.shape, X.dtype, y.shape, y.dtype)
			#torch.Size([32, 1, 64, 64]) torch.float32 torch.Size([32]) torch.int64
			break

softmax回归的从零开始实现

import torch
from IPython import display
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

初始化模型参数

和之前线性回归的例⼦⼀样，这⾥的每个样本都将⽤固定⻓度的向量表⽰。原始数据集中的每个样本都是28×28的图像。在本节中，我们将展平每个图像，把它们看作⻓度为784的向量。在后⾯的章节中，我们将讨论能够利⽤图像空间结构的特征，但现在我们暂时只把每个像素位置看作⼀个特征。回想⼀下，在softmax回归中，我们的输出与类别⼀样多。因为我们的数据集有10个类别，所以⽹络输出维度
为10。因此，权重将构成⼀个784 × 10的矩阵，偏置将构成⼀个1 × 10的⾏向量。与线性回归⼀样，我们将使⽤正态分布初始化我们的权重W，偏置初始化为0。

num_inputs = 784
num_outputs = 10
W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)

定义softmax操作

在实现softmax回归模型之前，我们简要回顾⼀下sum运算符如何沿着张量中的特定维度⼯作。如 2.3.6节和2.3.6节所述，给定⼀个矩阵X，我们可以对所有元素求和（默认情况下）。也可以只求同⼀个轴上的元素，即同⼀列（轴0）或同⼀⾏（轴1）。如果X是⼀个形状为(2, 3)的张量，我们对列进⾏求和，则结果将是⼀个具有形状(3,)的向量。当调⽤sum运算符时，我们可以指定保持在原始张量的轴数，⽽不折叠求和的维度。这将产⽣⼀个具有形状(1, 3)的⼆维张量。

X = torch.tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])
X.sum(0, keepdim=True), X.sum(1, keepdim=True)
#(tensor([[5., 7., 9.]]),
'''tensor([[ 6.],
         [15.]]))'''

def softmax(X):
	X_exp = torch.exp(X)
	partition = X_exp.sum(1, keepdim=True)
	return X_exp / partition # 这⾥应⽤了⼴播机制
X = torch.normal(0, 1, (2, 5))
X_prob = softmax(X)
X_prob, X_prob.sum(1)
'''(tensor([[0.2290, 0.1027, 0.1771, 0.0187, 0.4725],
[0.0509, 0.2083, 0.6785, 0.0430, 0.0193]]),
tensor([1., 1.]))'''

注意，虽然这在数学上看起来是正确的，但我们在代码实现中有点草率。矩阵中的⾮常⼤或⾮常⼩的元素可能造成数值上溢或下溢，但我们没有采取措施来防⽌这点。

定义模型

定义softmax操作后，我们可以实现softmax回归模型。下⾯的代码定义了输⼊如何通过⽹络映射到输出。注意，将数据传递到模型之前，我们使⽤reshape函数将每张原始图像展平为向量。

def net(X):
	return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)

接下来，我们实现 3.4节中引⼊的交叉熵损失函数。这可能是深度学习中最常⻅的损失函数，因为⽬前分类问题的数量远远超过回归问题的数量。回顾⼀下，交叉熵采⽤真实标签的预测概率的负对数似然。这⾥我们不使⽤Python的for循环迭代预测（这往往是低效的），⽽是通过⼀个运算符选择所有元素。下⾯，我们创建⼀个数据样本y_hat，其中包含2个样本在3个类别的预测概率，以及它们对应的标签y。有了y，我们知道在第⼀个样本中，第⼀类是正确的预测；⽽在第⼆个样本中，第三类是正确的预测。然后使⽤y作为y_hat中概率的索引，我们选择第⼀个样本中第⼀个类的概率和第⼆个样本中第三个类的概率。

	y = torch.tensor([0, 2])
	y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
	y_hat[[0, 1], y]
def cross_entropy(y_hat, y):
	return - torch.log(y_hat[range(len(y_hat)), y])
	'''由于y是⼀个⻓度为q的独热编码向量，所以除了⼀个项以外的所有项j都消失了。由于所有yˆj都是预测的概率，所以它们的对数永远不会⼤于0。'''
cross_entropy(y_hat, y)
#tensor([2.3026, 0.6931])

分类精度

def accuracy(y_hat, y):  #@save
    """计算预测正确的数量。"""
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1: #见下方解释
        y_hat = y_hat.argmax(axis=1) #找出y_hat中每行最大的数的索引号
    cmp = y_hat.type(y.dtype) == y #将y_hat和y进行比对，返回一个bool类型给cmp
    return float(cmp.type(y.dtype).sum()) #最后将cmp求和就是y_hat和y中相同元素个数
 
accuracy(y_hat, y) / len(y) #正确的比例的计算
#0.5

同样，对于任意数据迭代器data_iter可访问的数据集，我们可以评估在任意模型net的精度。

def evaluate_accuracy(net, data_iter):  #@save
    """计算在指定数据集上模型的精度。"""
    if isinstance(net, torch.nn.Module):
        net.eval()  # 将模型设置为评估模式
    metric = Accumulator(2)  # 两个结果：正确预测数、预测总数
    with torch.no_grad():
        for X, y in data_iter:
            metric.add(accuracy(net(X), y), y.numel())
    print(metric[0])
    print(metric[1])
    
    return metric[0] / metric[1]

训练

def train_epoch_ch3(net, train_iter, loss, updater):  #@save
    """训练模型一个迭代周期（定义见第3章）。"""
    # 如果是nn模具 将模型设置为训练模式
    if isinstance(net, torch.nn.Module):
        net.train()
    # 训练损失总和、训练准确度总和、样本数
    metric = Accumulator(3)长度为3的一个迭代器来累加
    for X, y in train_iter: #扫一遍数据
        # 计算梯度并更新参数
        y_hat = net(X) #求出预测值
        l = loss(y_hat, y) #求出损失
        if isinstance(updater, torch.optim.Optimizer): # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad() ##梯度设为0
            l.backward() #计算梯度
            updater.step() #对参数进行自更新
            metric.add(
                float(l) * len(y), accuracy(y_hat, y),
                y.size().numel())
        else:                                          # 使用定制的优化器和损失函数
            l.sum().backward()
            updater(X.shape[0])
            metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    return metric[0] / metric[2], metric[1] / metric[2] # 返回训练损失和训练准确率

在展⽰训练函数的实现之前，我们定义⼀个在动画中绘制数据的实⽤程序类Animator，它能够简化本书其余部分的代码。

class Animator:  #@save
    """在动画中绘制数据。"""
    def __init__(self, xlabel=None, ylabel=None, legend=None, xlim=None,
                 ylim=None, xscale='linear', yscale='linear',
                 fmts=('-', 'm--', 'g-.', 'r:'), nrows=1, ncols=1,
                 figsize=(3.5, 2.5)):
        # 增量地绘制多条线
        if legend is None:
            legend = []
        d2l.use_svg_display()
        self.fig, self.axes = d2l.plt.subplots(nrows, ncols, figsize=figsize)
        if nrows * ncols == 1:
            self.axes = [self.axes, ]
        # 使用lambda函数捕获参数
        self.config_axes = lambda: d2l.set_axes(
            self.axes[0], xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
        self.X, self.Y, self.fmts = None, None, fmts

    def add(self, x, y):
        # 向图表中添加多个数据点
        if not hasattr(y, "__len__"):
            y = [y]
        n = len(y)
        if not hasattr(x, "__len__"):
            x = [x] * n
        if not self.X:
            self.X = [[] for _ in range(n)]
        if not self.Y:
            self.Y = [[] for _ in range(n)]
        for i, (a, b) in enumerate(zip(x, y)):
            if a is not None and b is not None:
                self.X[i].append(a)
                self.Y[i].append(b)
        self.axes[0].cla()
        for x, y, fmt in zip(self.X, self.Y, self.fmts):
            self.axes[0].plot(x, y, fmt)
        self.config_axes()
        display.display(self.fig)
        display.clear_output(wait=True)

接下来我们实现⼀个训练函数，它会在train_iter访问到的训练数据集上训练⼀个模型net。该训练函数
将会运⾏多个迭代周期（由num_epochs指定）。在每个迭代周期结束时，利⽤test_iter访问到的测试数
据集对模型进⾏评估。我们将利⽤Animator类来可视化训练进度。

def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):  #@save
    """训练模型（定义见第3章）。"""
    animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
                        legend=['train loss', 'train acc', 'test acc'])
    for epoch in range(num_epochs):
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
        test_acc = evaluate_accuracy(net, test_iter)
        animator.add(epoch + 1, train_metrics + (test_acc,))
    train_loss, train_acc = train_metrics
    assert train_loss < 0.5, train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc

作为⼀个从零开始的实现，我们使⽤ 3.2节中定义的⼩批量随机梯度下降来优化模型的损失函数，设置学习率为0.1。

lr = 0.1

def updater(batch_size):
    return d2l.sgd([W, b], lr, batch_size)
def sgd(params, lr, batch_size):
    """Minibatch stochastic gradient descent."""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size#梯度*学习率/batch大小，所有的都可以这样更新
            param.grad.zero_()

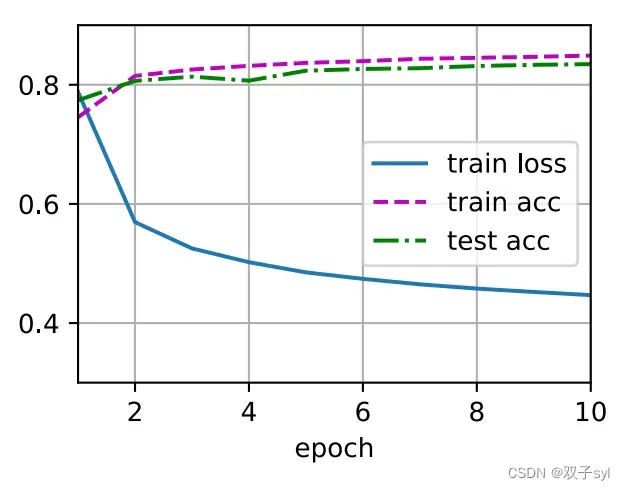
现在，我们训练模型10个迭代周期。请注意，迭代周期（num_epochs）和学习率（lr）都是可调节的超参数。通过更改它们的值，我们可以提⾼模型的分类精度。

num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)

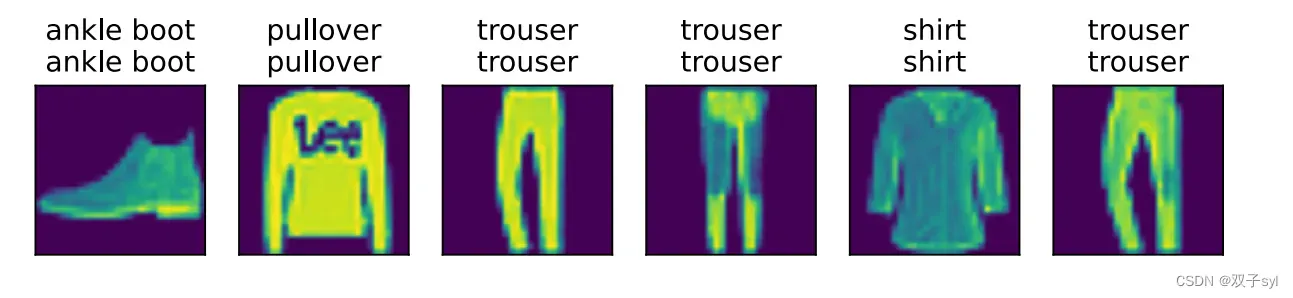
预测

现在训练已经完成，我们的模型已经准备好对图像进⾏分类预测。给定⼀系列图像，我们将⽐较它们的实际标签（⽂本输出的第⼀⾏）和模型预测（⽂本输出的第⼆⾏）。

def predict_ch3(net, test_iter, n=6):  #@save
    """预测标签（定义见第3章）。"""
    for X, y in test_iter:
        break
    trues = d2l.get_fashion_mnist_labels(y)
    preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
    titles = [true +'\n' + pred for true, pred in zip(trues, preds)]#zip打包到一起
    d2l.show_images(
        X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])

predict_ch3(net, test_iter)

softmax回归的简洁实现

import torch
from torch import nn
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

初始化模型参数

如我们在 3.4节所述，softmax回归的输出层是⼀个全连接层。因此，为了实现我们的模型，我们只需
在Sequential中添加⼀个带有10个输出的全连接层。同样，在这⾥Sequential并不是必要的，但它是
实现深度模型的基础。我们仍然以均值0和标准差0.01随机初始化权重。

# PyTorch不会隐式地调整输入的形状。因此，
# 我们在线性层前定义了展平层（flatten），来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

loss = nn.CrossEntropyLoss()

trainer = torch.optim.SGD(net.parameters(), lr=0.1)

num_epochs = 10
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)