前言
了解过word2vec或者youtubednn召回的话,都知道其负样本的选取是一个非均匀采样的过程(比如按照热度进行负采样)。此外,基于随机游走的graph embedding相关方法,如deepwalk,node2vec,eges等在随机游走构造序列的时候,也是一个非均匀采样。那我们如何自己实现一个非均匀采样呢?(之前腾讯、百度、美团面试被问到过!!!)
**场景:**给你一个数组,以及数组中每个位置的采样概率,如何实现产生符合这个概率分布的采样方法?
**例如:**一个随机事件包含四种情况 [a, b, c, d],每种情况发生的概率分别为:[0.3, 0.4, 0.2, 0.1]
本文主要介绍三种实现方法
- numpy自带的方法实现非均匀采样(平时自己小数据可以使用)
- 前缀和实现非均匀采样(面试中比较好实现的方法)
- Alias方法实现非均匀采样(graph embedding中邻居节点的采样会用到)
numpy自带的采样函数
import numpy as np
from collections import Counter
samples = ['a', 'b', 'c', 'd'] # 采样数组
probs = [0.3, 0.4, 0.2, 0.1] # 采样概率
s_num = 10000000 # 采样的数量
# size表示的是采样数量,p表示的是采样概率分布
s = np.random.choice(samples, size=s_num, p=probs)
cnt_dict = Counter()
for item in s:
cnt_dict[item] += 1
# 做归一化
cnt_list = cnt_dict.most_common(s_num)
prob_list = [(k, v / s_num) for k, v in cnt_list]
print(prob_list)
采样10000000次的结果:
[(‘b’, 0.400776), (‘a’, 0.298793), (‘c’, 0.199736), (‘d’, 0.100695)]
面试官让自己实现采样函数
**一种朴素的做法(先说做法再分析原因):**前缀和+二分
- 先计算概率分布数组的前缀和,记作S(其实这个前缀和数组也称为概率分布的累积分布)
- 通过一个随机数生成器,不断地生成[0,1]之间的数,然后在上述的前缀和数组中找到第一个大于等于随机数的位置,就是最终需要采样的位置。因为前缀和数组是一个单调递增的,所以可以使用二分法在log(n)的复杂度完成
import random
from collections import defaultdict
samples = ['a', 'b', 'c', 'd'] # 采样数组
probs = [0.3, 0.4, 0.2, 0.1] # 采样概率
# 计算前缀和数组
S = []
t = 0
for p in probs:
t += p
S.append(t)
print(S)
# 使用二分法在前缀和中采样
def bs(random_num):
l, r = 0, len(S) -1
while l < r:
mid = (l + r) // 2
if S[mid] >= random_num:
r = mid
else:
l = mid + 1
return r
s_num = 10000000 # 采样的数量
cnt_dict = Counter()
for _ in range(s_num):
a = random.uniform(0, 1)
cnt_dict[samples[bs(a)]] += 1
cnt_list = cnt_dict.most_common(s_num)
prob_list = [(k, v / s_num) for k, v in cnt_list]
print(prob_list)
输出结果:
[0.3, 0.7, 0.8999999999999999, 0.9999999999999999]
[(‘b’, 0.400776), (‘a’, 0.298793), (‘c’, 0.199736), (‘d’, 0.100695)]
从上面的采样结果可以看出,结果是符合预期的
下面简单介绍一下,为什么这么做是正确的,为了方便计算,我们把概率分布P设置为: [0.3, 0.4, 0.2, 0.1]
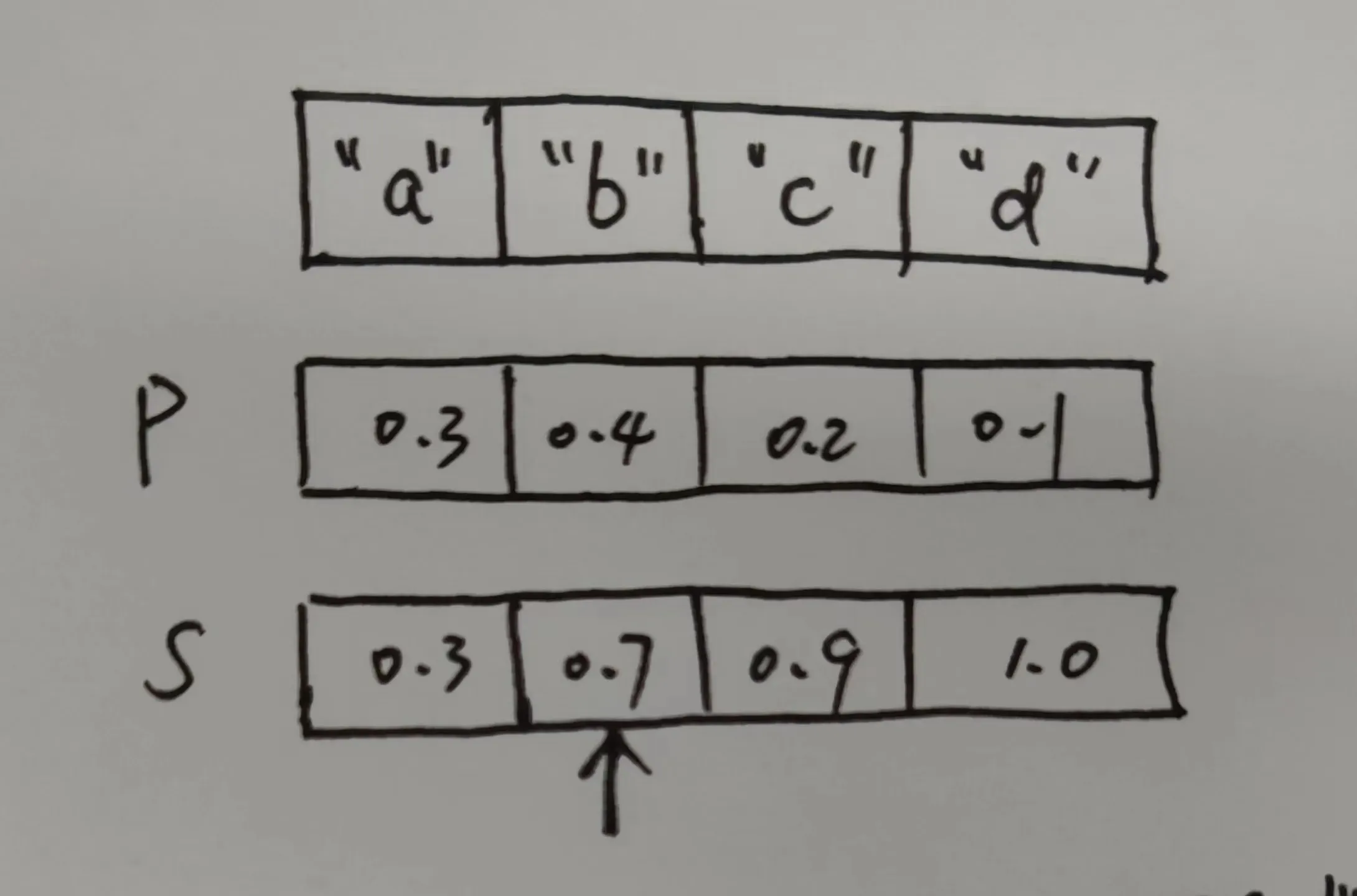
对于通过均匀分布生成的[0, 1]之间的随机数x, 以在S数组中找到的第一个大于等于x的下标作为采样结果的采样方式,x需要满足什么条件才能采样到数组的第二个位置呢?(需要注意的是,x是在S数组中进行二分。)可以明显看出,当 0.3<x<=0.7的时候通过二分得到的下标在数组S的第二个位置,而生成的随机数生成这个范围的数的概率刚好是0.4,这和概率分布P的第二个位置需要的采样概率是相同的,这就是上面为什么使用前缀和+二分的方法来采样的原因。
能不能用O(1)的时间复杂度实现采样
这里主要介绍Alias采样方法了。这里的内容主要是参考国外的一个博客,里面的图画的非常清晰,下面来分析一下如何通过O(1)的时间复杂度实现。
为了更好的与图片上的概率值对应,将概率分布修改为:[1/2, 1/3, 1/12,1/12],并用下面的四个柱子表示采样分布。
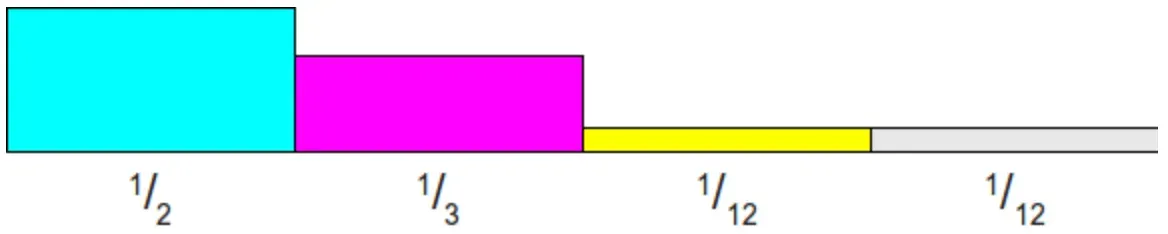
然后每个柱子上的概率值乘以N(N表示的是柱子的数量),先不要想为什么,先继续看下去!
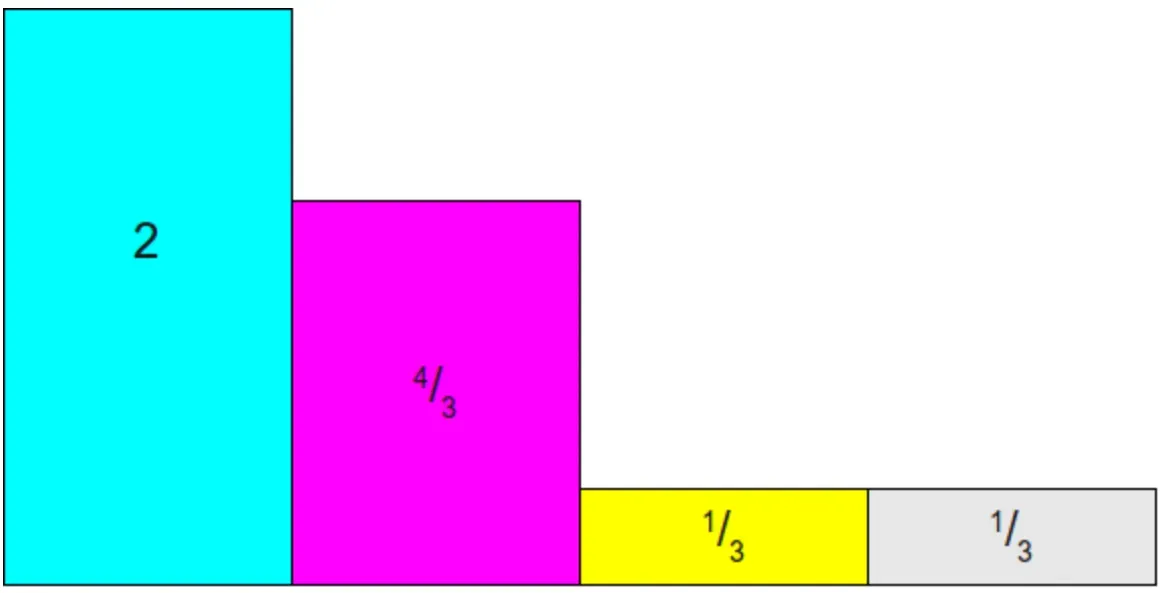
然后将比较高的柱子,切出一部分填到低柱子上,让每个柱子的高度都变成1,如下图所示,棕色的就是我们需要填充的
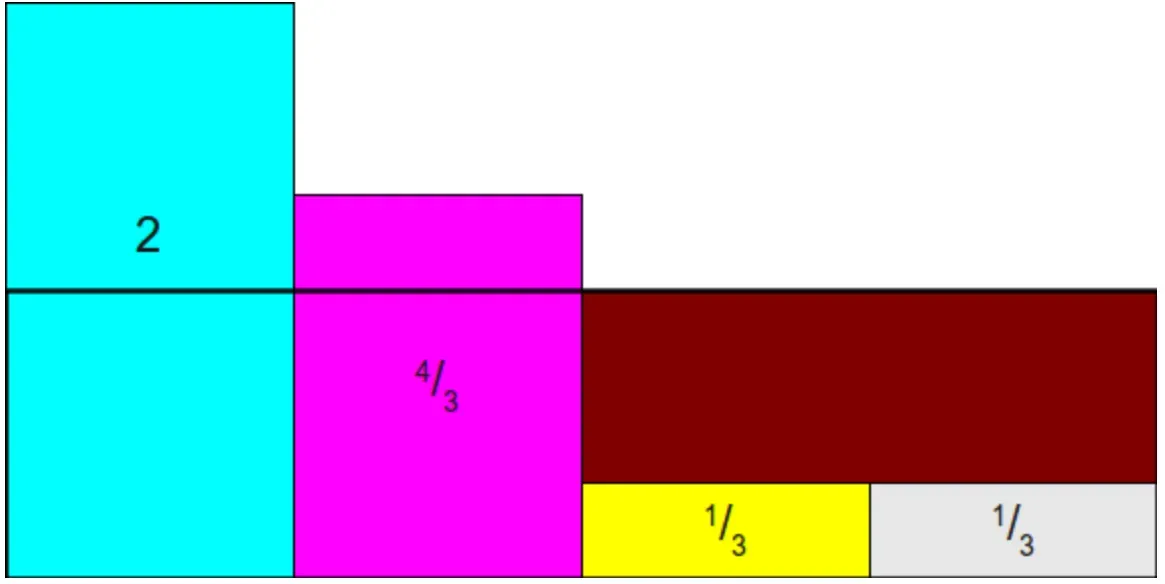
先从第一个柱子中拿2/3放到最后一个柱子上,然后就变成下面这个图了
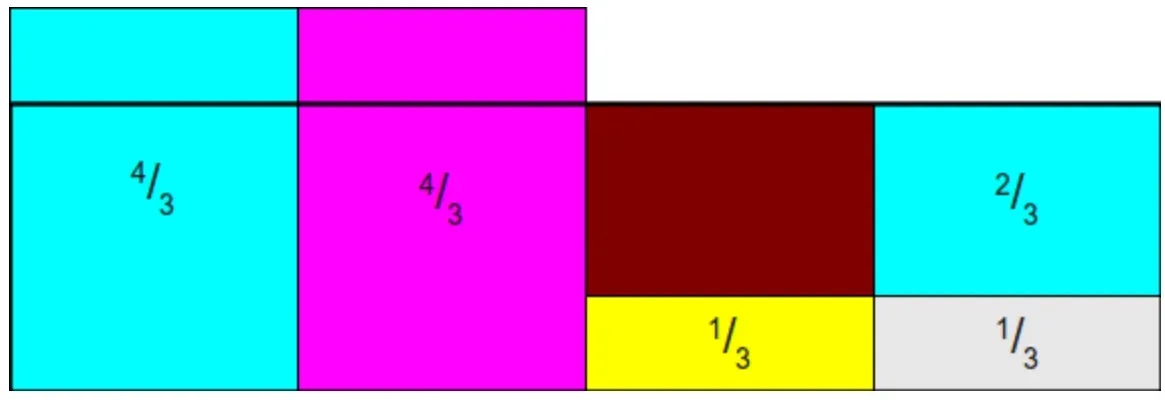
然后此时会发现,好像只需要将第一个柱子的1/3和第二个柱子的1/3都放到第三个柱子上就行了,但是Alias算法需要保证每个位置上最多只能包含两个柱子的信息。所以这里可以先将第一个柱子的2/3放到第三个柱子上,然后将第二个柱子的1/3放到第一个柱子上,如下图所示:
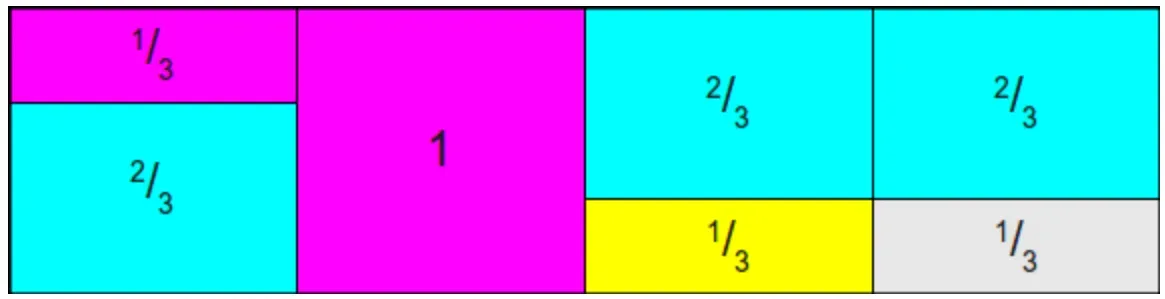
这样一来,柱子的划分任务就完成了,这里总结来说就是,先在原概率分布上乘以柱子的数量(事件的数量),然后将柱子的高度都转换成1,并且每个位置的柱子最多只能包含两个柱子的信息,这些是使用Alias方法的前提。
下面介绍Alias方法的具体实施步骤(假如最原始四个柱子对应的事件分别为[“a”, “b”, “c”, “d”]):
- 对于原始的概率分布表P=[1/2, 1/3,1/12,1/12], 先通过上述方法,将概率分布拉伸成一个1xN的Alias表,就是上面的最后一个图的样子。(具体如何实现的,后面再详细的分析)
- 构建两个数组,第一个数组Prob=[2/3, 1, 1/3, 1/3],每个位置表示的是当前位置事件占的百分比。比如数组中的第一个位置是2/3,表示的是,当前柱子取到事件”a”(第一个位置对应的事件)的百分比
- 第二个数组是,Alias=[“b”, none, “a”, “a”],这个数组中的每个位置表示的是,除了当前位置本身所表示的事件以外的另一个事件。例如,对于第一个柱子来说(看上面的最后一个图),这个柱子在原来的柱子中是只表示事件”a”的,但是因为柱子的高度的重新分配,引入了1/3的”b”,所以当前位置除了事件”a”以外的另一个事件就是”b”,其他的依次类推
- 产生两个随机数,第一个随机数i在[1, N]之间,确定当前选择哪一个柱子,第二个随机数在[0,1]之间,判断当前随机数与Prob[i]的大小,如果小于Prob[i]则采样第i个位置的事件,否则采样Alias[i]对应的事件
下面分析一下为什么上面那么做是对的,下面分别分析每个事件的采样概率:
- “a”(蓝色)的概率:1/4 * 2 / 3 + 1 /4 * 2/3 + 1/4 * 2/3 = 1/4 * 2 = 1/2
- “b”(紫色)的概率:1/4 * 1/3 + 1/4 * 1 = 1/4 * (4/3) = 1/3
- “c”(黄色)的概率:1/4 * 1/3 = 1/12
- “d”(灰色)的概率:1/4 * 1/3 = 1/12
根据Alias方法采样,每个事件的采样概率和预期的采样概率是相同的,所以这种采样方式是有效的。此外,Alias采样方法每次采样结果最多需要采样两次就一定能够得到采样结果。其实这里还可以通过拒绝采样的思路来实现,离散非均匀采样,但是拒绝采样会浪费很多采样机会,效率不如Alias采样方法。
那如何构建Alias表呢?Alias表一定存在嘛?
- 先简单说一下Alias表的构建,通过上面一系列图的操作,可以发现,每次其实都是在拿一个高度大于1的柱子,切出一块填补到一个高度小于1的柱子,但是需要注意,高度大于1的柱子填补了其他柱子之后是可能会变成高度小于1的柱子的。其实在代码实现的过程中也是这个思路,只不过为了高效的完成前面说的用高度大于1的柱子去填补高低小于1的柱子,会使用两个队列small_queue和large_queue,分别将所有高度小于1的柱子和所有高度都大于1的柱子。每次只需要从small_queue和large_queue中各拿出一个来,从高柱子中切一块将矮柱子补成长度为1的柱子,一次执行下去。
- 通过上述的操作我们思考一下是否一定有解呢?也就是上面的循环不会是死循环。其实这里是可以通过数学证明出来,一定是有解的(详细证明可以参考最后面给出的英文资料)。这里我们简单分析一下为什么有解,首先对于一个离散的概率分布有N个不同的取值(所有概率值加起来为1),每个位置先乘以概率分布离散取值的数量N,这个时候通过上述方法来切高柱子补矮柱子,按照上述的做法,每次都会拿一个高柱子来填补低柱子至高度为1(首先这一步是肯定可以实现的,因为高柱子的高度都是大于1的),填补完矮柱子之后,整个分布中就多了一个高度为1的柱子,按照这个逻辑下去,执行N次所有的柱子的高度都是1了。这里需要注意的是,高柱子填切割出来填补矮柱子之后,高柱子也可能变成矮柱子,需要将这里产生的矮柱子也添加到small_queue中,那这种情况不会导致死循环嘛?答案是不会的,因为只要存在一个矮柱子就一定会至少存在一个高柱子,这是所有柱子高度总和决定的,所以就一定可以把那个矮柱子填补到1。
下面简单来看一下代码如何实现Alias表是如何构建的吧!
import random
from collections import Counter
def create_alias_tables(p_list):
"""
:param p_list:概率列表,列表的和为1
:return:返回一个accept_prob概率数组,和alias_index事件数组
"""
N = len(p_list) # 事件总数
# 初始化概率数组和事件数组
accept_prob, alias_index = [0] * N, [0] * N
# 定义两个队列
small_queue, large_queue = [], []
# 概率值乘以事件数,其结果与1进行比较,分别大于1和小于1的
# 结果对应的索引添加到上述定义的两个队列中
for i, p in enumerate(p_list):
p *= N
# 概率数组中的初试值,后面会重新分配
accept_prob[i] = p
if p < 1.0:
small_queue.append(i)
else:
# 高度为1的柱子放在了large_queue中
large_queue.append(i)
# 遍历small_queue和large_queue, 每次都从中各取一个,用大的填补小的
# 因为我们把高度为1的柱子放在了large中,所以,最终small_queue会为空
while small_queue and large_queue:
small_index = small_queue.pop()
large_index = large_queue.pop()
# 更新alias事件表, 因为我们是用大的填补小的,小的柱子才是
# 对应着原来的事件,看填充过程的图片可能会更明显
alias_index[small_index] = large_index
# 更新高柱子的高度, 就是减去填补矮柱子到1的高度
accept_prob[large_index] = accept_prob[large_index] - (1 - accept_prob[small_index])
# 矮柱子的accept为什么不需要修改概率?是因为矮柱子留下的概率,就是当前位置对应事件的概率
# 即使由高柱子变成了矮柱子,那也表示的是采样到当前柱子且采样到高柱子的概率是当前的概率值
# 判断当前高柱子是否还是高柱子, 注意如果当
if accept_prob[large_index] < 1.0:
small_queue.append(large_index)
else:
large_queue.append(large_index)
return accept_prob, alias_index
def alias_sample(accept_prob, alias_index):
"""
:param accept_prob: 概率数组
:param alias_index: 事件数组
:return 返回采样的位置
"""
# 先从所有柱子中选择一个柱子
N = len(accept_prob)
# 随机生成一个[0,(N-1)]的数
random_n = random.randint(0, N-1)
# 再随机生成一个 [0-1]之间的数
random_i = random.random()
# 判断当前柱子的accpet_prob值与生成的random_i的大小
if random_i <= accept_prob[random_n]:
return random_n
return alias_index[random_n]
测试采样效果
samples = ['a', 'b', 'c', 'd'] # 采样数组
probs = [0.3, 0.4, 0.2, 0.1] # 采样概率
accept_prob, alias_index = create_alias_tables(probs)
s_num = 1000000 # 采样的数量
cnt_dict = Counter()
for _ in range(s_num):
a = alias_sample(accept_prob, alias_index)
cnt_dict[samples[a]] += 1
cnt_list = cnt_dict.most_common(s_num)
prob_list = [(k, v / s_num) for k, v in cnt_list]
print(prob_list)
输出结果:
[(‘b’, 0.399794), (‘a’, 0.299652), (‘c’, 0.200755), (‘d’, 0.099799)]
总结

本文主要从一个非均匀采样的问题出发,分别使用numpy自带的方法、前缀和+二分以及Alias方法实现了满足给定采样分布的采样函数。其中,对于第二种采样方法在面试中比较容易被问到,第三种方法在Graph Embedding中对邻居节点的采样会被经常用到,第一种也可以在自己平时的工作中直接调用。
如果文章对你有帮助,欢迎扫码关注微信公众号!或者微信搜索 若如意

参考资料
- Github: https://github.com/ruyiluo/ryluo_notes
- Darts, Dice, and Coins: Sampling from a Discrete Distribution
- 【数学】时间复杂度O(1)的离散采样算法—— Alias method/别名采样方法
- GraphEmbedding – Alias 采样图文详解
文章出处登录后可见!
