系列文章目录

提示：这里可以添加系列文章的所有文章的目录，目录需要自己手动添加
例如：第一章 Python 机器学习入门之pandas的使用

提示：写完文章后，目录可以自动生成，如何生成可参考右边的帮助文档

前言

提示：这里可以添加本文要记录的大概内容：

例如：随着人工智能的不断发展，机器学习这门技术也越来越重要，很多人都开启了学习机器学习，本文就介绍了机器学习的基础内容。

提示：以下是本篇文章正文内容，下面案例可供参考

一、相机标定

1. 概念
   在图像测量过程以及机器视觉应用中，为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系，必须建立相机成像的几何模型，这些几何模型参数就是相机参数。在大多数条件下这些参数必须通过实验与计算才能得到，这个求解参数（内参、外参、畸变参数）的过程就称之为相机标定。
   2.相机成像
   
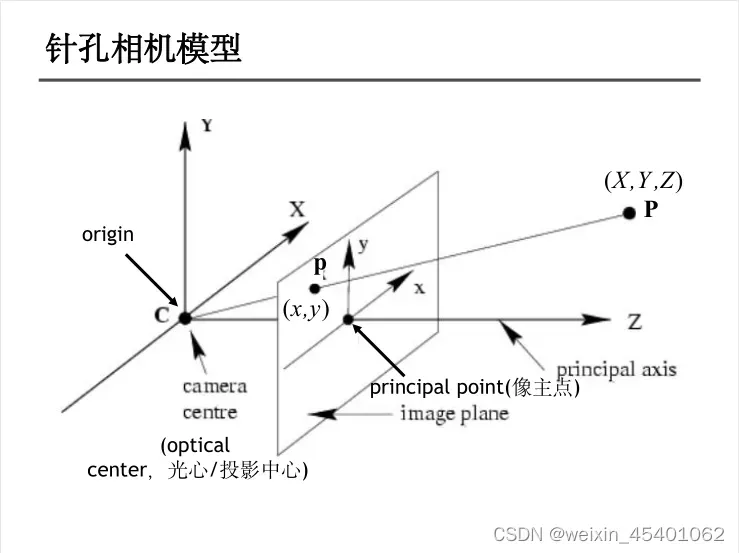
   相机成像系统中，有四个坐标系： 相机坐标系 、 图像坐标系、图像像素坐标系 和 世界坐标系。
   世界坐标系：也称参考坐标系，是用户定义的三维世界的坐标系，为了描述目标物在真实世界里的位置而被引入 。Pw(Xw,Yw,Zw)
   相机坐标系：以相机的光心为坐标原点， X 轴和 Y 轴分别平行于图像坐标系的 X 轴和 Y 轴， 相机的光轴为 Z 轴。Pc(Xc,Yc,Zc)
   图像坐标系： 以图像平面的中心为坐标原点， X 轴和 Y 轴分别平行于图像平面的两条垂直边， 用( x , y )表示其坐标值。 图像坐标系是用物理单位（例如毫米） 表示像素在图像中的位置。
   像素坐标系： 以图像平面的左上角顶点为原点， X 轴和 Y 轴分别平行于图像坐标系的 X 轴和 Y 轴， 用(u , v )表示其坐标值,单位是像素。
   2.1世界坐标系到相机坐标系
   
   2.2相机坐标系–>图像坐标系
   真实世界中的某点会投影在相机的成像平面上， 图像坐标系和相机坐标系下坐标的 关系如下：
   
   2.3图像坐标系–>像素平面坐标系
   
   
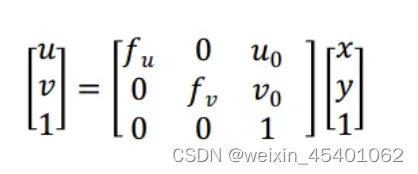
   综上所述，某个物点的世界坐标到像素坐标的关系如下:
   

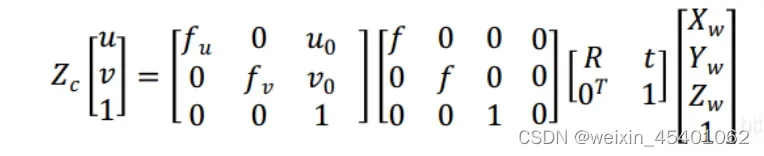
即单点无畸变的相机成像模型如下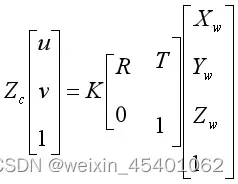

外参矩阵如下：

实际上由于相机光学系统存在加工和装配的误差， 透镜就并不能满足物和像成相似三角形的关系， 所以相机图像平面上实际所成的像与理想成像之间会存在畸变。
3.畸变
畸变包括径向畸变和切向畸变。
径向畸变公式（3阶）如下：

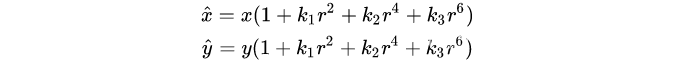
切向畸变公式如下：

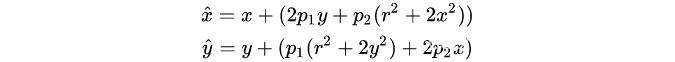
两种(x,y)表示分别为理想的无畸变的归一化的图像坐标、畸变后的归一化图像坐标， 为图像像素点到图像中心点的距离，即 获得相机的畸变参数：进而对拍摄的图片进行去畸变处理。
2.畸变模型

二、张正友标定法

张正友标定法利用如下图所示的棋盘格标定板，在得到一张标定板的图像之后，可以利用相应的图像检测算法得到每一个角点的像素坐标(u,v)

张正友标定法将世界坐标系固定于棋盘格上，则棋盘格上任一点的物理坐标 Z=0，由于标定板的世界坐标系是人为事先定义好的，标定板上每一个格子的大小是已知的，我们可以计算得到每一个角点在世界坐标系下的物理坐标(X,Y,Z=0)。
我们用一下的数：每一个角点的像素坐标 (u,v) 、每一个角点在世界坐标系下的物理坐标(X,Y,Z=0)，来进行相机的标定，获得相机的内外参矩阵、畸变参数。
1.相机标定的步骤
(1). 打印一张棋盘格A4纸张（黑白间距已知），并贴在一个平板上
(2). 针对棋盘格拍摄若干张图片（一般10-20张）
(3). 在图片中检测特征点（Harris角点）
(4). 根据角点位置信息及图像中的坐标，求解Homographic矩阵
(5). 利用解析解估算方法计算出5个内部参数，以及6个外部参数
(6). 根据极大似然估计策略，设计优化目标并实现参数的refinement
2.代码

# coding=utf-8
import cv2
import numpy as np
import glob
criteria = (cv2.TERM_CRITERIA_MAX_ITER | cv2.TERM_CRITERIA_EPS, 30, 0.001)
# 前者均表示迭代次数达到最大次数时停止
# 后者表示角点位置变化的最小值已经达到最小值时停止
# 世界坐标系是人为控制的z=0,使用x，y，矩阵
objp = np.zeros((11 * 8, 3), np.float32)
objp[:, :2] = np.mgrid[0:11, 0:8].T.reshape(-1, 2)  # 将世界坐标系建在标定板上，所有点的Z坐标全部为0，所以只需要赋值x和y

obj_points = []  # 存储3D点，真实坐标系下的三维点坐标
img_points = []  # 存储2D点  图像平面的坐标

images = glob.glob('./qipan/*.jpg')
i=0
# 读取图片
# 灰度化处理，提高程序运行效率
for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    size = gray.shape[::-1]
    ret, corners = cv2.findChessboardCorners(gray, (11, 8), None) # Homographic矩阵,可通过最小二乘从角点世界坐标到图像坐标的关系求解
    # print(gray)
    # 找棋盘格角点
    # ret 找没找到角点坐标
    # corners 角点像素坐标系的坐标
    print('corners',corners)
    if ret:

        obj_points.append(objp)

        corners2 = cv2.cornerSubPix(gray, corners, (5, 5), (-1, -1), criteria)  # 在原角点的基础上寻找亚像素角点
        # 逆函数
        # print(corners2)
        if [corners2]:
            img_points.append(corners2)
        else:
            img_points.append(corners)

        cv2.drawChessboardCorners(img, (11, 8), corners, ret)  # 记住，OpenCV的绘制函数一般无返回值
        i += 1
        cv2.imwrite('qipan' + str(i) + '.jpg', img)
        cv2.waitKey(1500)

print(len(img_points))
print(size)
cv2.destroyAllWindows()

# 标定 相机匹配
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)

print("ret:", ret)
print("mtx:", mtx) # 内参数矩阵
print("dist:", dist)  # 畸变系数   distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print("rvecs:", rvecs)  # 旋转向量  # 外参数
print("tvecs:", tvecs ) # 平移向量  # 外参数

print("-----------------------------------------------------")
# 图片的扭曲

img = cv2.imread('.\qipan\D.jpg')
h, w = img.shape[:2]
print(h)
print(w)
# 内参，扭曲，得到新的相机内参数，roi是一个感兴趣的区域
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),1,(w,h))#显示更大范围的图片（正常重映射之后会删掉一部分图像）
print (newcameramtx)
print("------------------使用undistort函数-------------------")
dst = cv2.undistort(img,mtx,dist,None,newcameramtx)
# 尺寸感兴趣的范围
x,y,w,h = roi
dst1 = dst[y:y+h,x:x+w]
cv2.imwrite('D1.jpg', dst1)
print ("方法一:dst的大小为:", dst1.shape)

# 反投影误差
total_error = 0
for i in range(len(obj_points)):
    imgpoints2, _ = cv2.projectPoints(obj_points[i], rvecs[i], tvecs[i], mtx, dist)
    error = cv2.norm(img_points[i],imgpoints2, cv2.NORM_L2)/len(imgpoints2)
    total_error += error
print(("total error: "), total_error/len(obj_points))

三、实验结果
1.正拍

1.1角点检测结果

1.2
内参结果截图

1.3外参结果
旋转向量

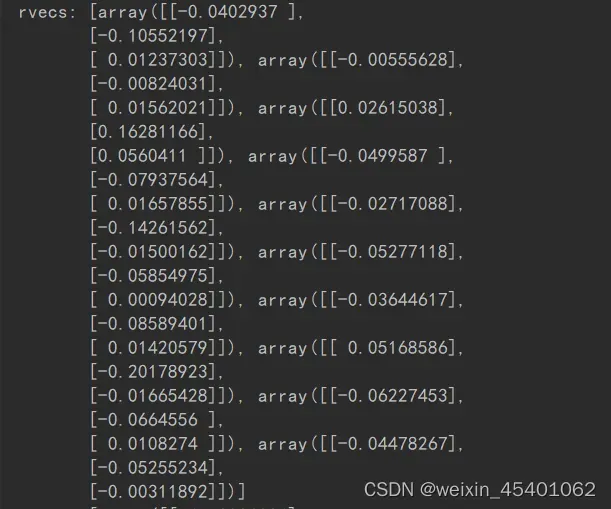
平移向量

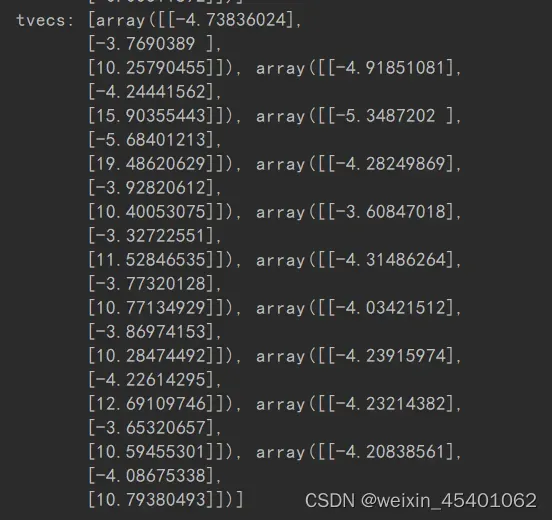
1.4畸变处理
通过反投影误差，我们可以来评估结果的好坏，越接近0，说明结果越理想。通过之前计算的内参数矩阵、畸变系数、旋转矩阵和平移向量，使用cv2.projectPoints()计算三维点到二维图像的投影，然后计算反投影得到的点与图像上检测到的点的误差，最后计算一个对于所有标定图像的平均误差即反投影误差。我的反投影误差求出来是0.04363810070344593，属于比较小的误差，。
选取其中的一张图尝试进行（图片如下），在校准下方角有一定的畸变，而校准后的图片得到了改善。
原图

校正后

2.旋转右拍摄

2.1角点检测结果

2.2内外参数截图
内参数矩阵

外参数矩阵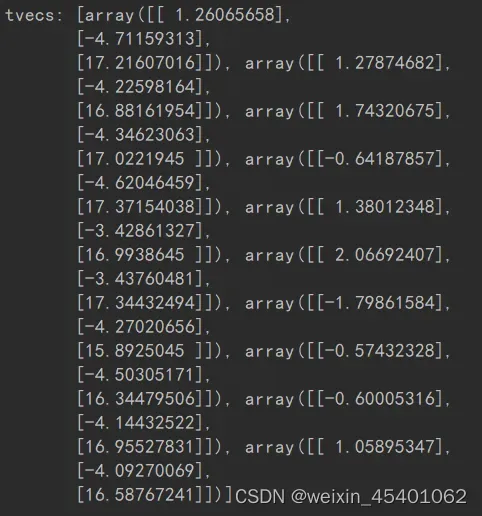

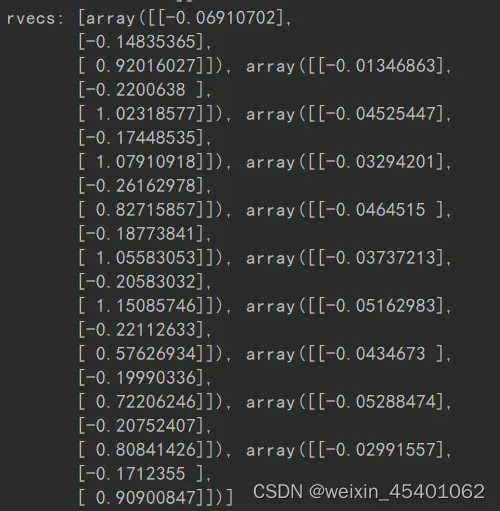
2.3畸变处理
原图

校正后

反投影误差

3.混合
使用同一相机从不同的位置，不同的角度，不同的姿态，拍摄标定板的多张照片

3.1角点检测结果

3.2内外参数截图
内参数矩阵

外参矩阵

rvecs: [array([[-0.50181511],
       [-0.58275314],
       [ 1.84395831]]), array([[-0.50940568],
       [-0.56582495],
       [ 1.81061372]]), array([[-0.17217173],
       [-0.5685897 ],
       [ 0.89052364]]), array([[-0.18687764],
       [-0.59000454],
       [ 1.05031761]]), array([[-0.10338737],
       [-0.67857455],
       [ 0.80030277]]), array([[-0.18507589],
       [-0.60064277],
       [ 1.0275061 ]]), array([[-0.1878927 ],
       [-0.61174449],
       [ 1.12301821]]), array([[-0.61260448],
       [-0.55170016],
       [ 2.07697315]]), array([[-0.0543254 ],
       [-0.14563584],
       [ 0.01335128]]), array([[-0.00476324],
       [-0.01027563],
       [ 0.01576322]]), array([[-0.63521287],
       [-0.56946534],
       [ 2.09378256]]), array([[0.00803354],
       [0.20916588],
       [0.05284632]]), array([[-0.06579242],
       [-0.10949469],
       [ 0.01711036]]), array([[-0.03745391],
       [-0.19023287],
       [-0.01347029]]), array([[-0.06973588],
       [-0.08076385],
       [ 0.00120697]]), array([[-0.04854451],
       [-0.11763109],
       [ 0.01498961]]), array([[ 0.0460515 ],
       [-0.26203937],
       [-0.01241838]]), array([[-0.08308311],
       [-0.09146447],
       [ 0.01103173]]), array([[-0.05844778],
       [-0.07184236],
       [-0.00282397]])]
tvecs: [array([[-6.6649839],
       [-7.6886037],
       [43.474129 ]]), array([[-5.24600961],
       [-6.25467604],
       [37.36064738]]), array([[-10.71293494],
       [ -7.89203221],
       [ 41.1188728 ]]), array([[-10.23735635],
       [ -7.53673453],
       [ 41.2244755 ]]), array([[-12.86116161],
       [ -7.88233413],
       [ 41.91742902]]), array([[-10.59289608],
       [ -6.61566789],
       [ 41.19104789]]), array([[-10.2204656 ],
       [ -6.71167876],
       [ 42.31737117]]), array([[-5.67793381],
       [-5.61699311],
       [41.26323866]]), array([[-4.86005435],
       [-3.51547087],
       [14.34075638]]), array([[-5.13153544],
       [-3.84791725],
       [22.28513989]]), array([[-7.38991746],
       [-4.79626297],
       [45.06028544]]), array([[-5.55118314],
       [-5.1914566 ],
       [27.11322914]]), array([[-4.41561876],
       [-3.67033022],
       [14.54608163]]), array([[-3.74259015],
       [-3.04037169],
       [16.1390334 ]]), array([[-4.45695826],
       [-3.50530136],
       [15.07380171]]), array([[-4.16395656],
       [-3.61442892],
       [14.39191902]]), array([[-4.35322998],
       [-3.90338238],
       [17.82740929]]), array([[-4.37212465],
       [-3.38968211],
       [14.82341464]]), array([[-4.35136171],
       [-3.81854103],
       [15.10956092]])]
       total error:  0.08829283413513649

3.3畸变处理